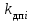Лабораторная работа 4 Моделирование интеллектуальной системы манипулятора 1 Цель работы
 Скачать 1.1 Mb. Скачать 1.1 Mb.
|
|
Лабораторная работа № 4 Моделирование интеллектуальной системы манипулятора 4.1 Цель работы Расчет параметров и моделирование интеллектуальной системы манипулятора. 4.2 Краткие сведения об объекте моделирования Функциональная схема системы управления движением звеньев манипулятора показана на рис. 4.1. 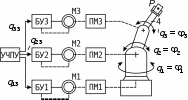 Рис. 4.1. Функциональная схема управления манипулятором Математическая модель манипулятора учитывает кинематические связи, динамические взаимодействия инерционных, центробежных, кориолисовых и гравитационных моментов, внешние моменты исполнительных механизмов. В исполнительных устройствах используются двигатели постоянного и переменного токов. При построении математической модели приняты следующие допущения: отсутствуют люфты между валами двигателей и звеньями манипулятора; отсутствуют упругие деформации в приводах, передаточных механизмах и звеньях манипулятора; ошибки квантования на выходе цифровых систем управления электроприводами незначительны. Динамика механической части манипулятора описывается нелинейным векторно-матричным уравнением 2-го порядка:
где 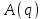 матрица коэффициентов инерции, зависящая от вектора матрица коэффициентов инерции, зависящая от вектора 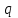 ; ; 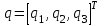 вектор обобщенных координат; вектор обобщенных координат; 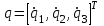 вектор обобщенных скоростей; вектор обобщенных скоростей;  вектор моментов сил инерции, зависящий от векторов вектор моментов сил инерции, зависящий от векторов 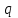 , , 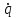 ; ; 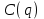 вектор моментов сил тяжести, зависящий от вектора вектор моментов сил тяжести, зависящий от вектора 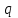 ; ;  вектор моментов трения, вектор моментов трения, 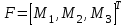 вектор обобщенных моментов. вектор обобщенных моментов.В развернутом виде система уравнений (4.1) приведена в [5] и в [6]. Подробный вывод уравнений дан в [6]. Динамические характеристики манипулятора зависят от его текущей пространственной конфигурации и изменяются в процессе манипулирования. Исходное расположение звеньев задается соответствующими начальными условиями для системы (4.1). При исследовании замкнутой системы управления манипулятором по координатам 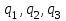 уравнение (4.1) необходимо дополнить уравнениями электроприводов, регуляторов координат, по которым реализуются обратные связи. Ориентируясь на трехконтурные системы каждой из координат уравнение (4.1) необходимо дополнить уравнениями электроприводов, регуляторов координат, по которым реализуются обратные связи. Ориентируясь на трехконтурные системы каждой из координат 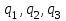 , выполненных по принципу подчиненного управления, необходимо для каждого из каналов управления дополнить уравнение (4.1) уравнениями регуляторов положения, скорости и тока электродвигателя соответственно. Структурная схема системы управления трехзвенным манипулятором показана на рис. 4.2. , выполненных по принципу подчиненного управления, необходимо для каждого из каналов управления дополнить уравнение (4.1) уравнениями регуляторов положения, скорости и тока электродвигателя соответственно. Структурная схема системы управления трехзвенным манипулятором показана на рис. 4.2.Расчет параметров звеньев выполняется в Mathcad по следующим формулам: 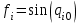 ; ;  ; ; 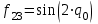 ; ; 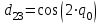 ; ; 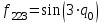 ; ;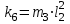 ; ;  ; ; 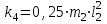 ; ;  ; ; 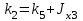 ; ; ; ; 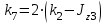 ; ; 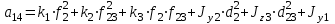 ; ;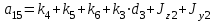 ; ; 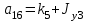 ; ; 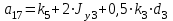 ; ;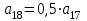 ; ; 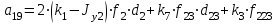 ; ; ; ; 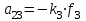 ; ; 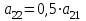 ; ; 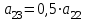 ; ;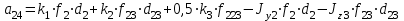 ; ;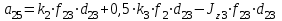 ; ; 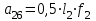 ; ; 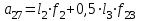 ; ; 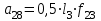 ; ; 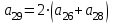 ; ;  ; ;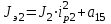 ; ;  . .Расчет параметров регуляторов выполняется в Mathcad по следующим формулам: 1. Регулятор тока: 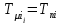 ; ; 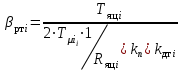 ; ; 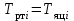 . .  Рис. 4.2. Структурная схема системы управления трехзвенным манипулятором 2. Регулятор скорости: 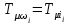 ; ; 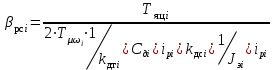 ; ; 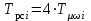 . .3. Регулятор положения: 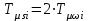 ; ; 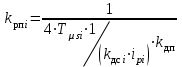 4.3 Порядок выполнения работы 1. Ознакомиться с техническим описанием интеллектуальной системы робота. 2. Составить математическую модель интеллектуальной системы робота. 3. Рассчитать систему управления в соответствии с вариантом задания (табл. 4.1, 4.2). Табл. 4.1. Параметры звеньев и передаточных механизмов манипулятора
Табл. 4.2. Параметры элементов систем управления движением звеньев манипулятора
4. Выполнить исследование динамических характеристик системы управления при заданных управляющих и возмущающих воздействиях, видах регуляторов, номерах звеньев манипулятора. 5. Выполнить исследования взаимодействия сепаратных систем управления звеньями манипулятора. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

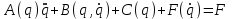 ,
, Параметр
Параметр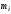 ,
,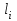 ,
,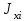 ,
,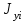 ,
, ,
, ,
,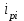
 ,
,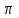 /6
/6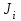 ,
, ,
,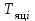 ,
,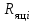 Ом
Ом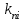
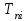 ,
, ,
,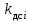 ,
,