Лабораторная работа 2 Денис. Лабораторная работа 41к определение горизонтальной составляющей магнитного поля земли что такое магнитное поле

• Название: Лабораторная работа 41к определение горизонтальной составляющей магнитного поля земли что такое магнитное поле
• Дата: 23.02.2022
• Размер: 0.76 Mb.
• Имя файла: Лабораторная работа 2 Денис.docx
• Тип: Лабораторная работа; #371541

Лабораторная работа № 41-к

ОПРЕДЕЛЕНИЕ ГОРИЗОНТАЛЬНОЙ СОСТАВЛЯЮЩЕЙ МАГНИТНОГО ПОЛЯ ЗЕМЛИ

1. 
   Что такое магнитное поле?
   

Магнитное поле – особый вид материи, посредством которого осуществляется взаимодействие движущихся зарядов (токов) и намагниченных тел

2. 
   Характеристики магнитного поля.
   

Магнитная индукция, магнитный поток, сила Ампера, сила Лоренца

3. 
   Закон Био-Савара-Лапласа. Принцип суперпозиции полей.
   

Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: поле системы токов равно сумме полей, создаваемых каждым током.

4. 
   Применение закона Био-Савара-Лапласа для расчёта магнитного поля в центре кругового тока. Магнитный момент контура с током.
   

Чтобы найти поле в центре кольца с током, мысленно разобьем его на множество элементов тока (см. рис. 2а).



Каждый элемент тока, согласно закону Био-Савара-Лапласа, создает магнитное поле с индукцией, определяемой формулой


Прежде всего проверим, как направлены векторы, создаваемые каждым элементом тока. Пользуясь приведенным выше правилом правого винта для определения направления, легко убедиться, что в центре кольца все векторы направлены в одну сторону, перпендикулярно плоскости кольца. Следовательно, векторную сумму можно заменить арифметической, и для магнитной индукции в центре кольца получаем на основе (2) выражение:



Из геометрии задачи видно, что



Вынося из-под знака интеграла постоянные величины , получаем:



Интеграл по окружности равен ее длине:



Таким образом, магнитная индукция в центре кольца равна:

(3)

Вектор магнитной индукции направлен перпендикулярно плоскости кольца, направление вектора определяется по правилу правого винта для кольцевого тока: винт установить перпендикулярно плоскости кольца и поворачивать по направлению тока в кольце, направление поступательного движения винта покажет направление вектора .

Направление вектора магнитного момента контура с током совпадает с направлением положительной нормали к контуру

5. 
   Сила Ампера. Механический момент, действующий на рамку с током в магнитном поле.
   

Французский ученый Ампер установил, что на элемент тока в магнитном поле действует сила , где I – сила тока.

Ф ормула (1) является математическим выражением закона Ампера, ее иллюстрирует рисунок

Механические моменты сил и относительно оси, лежащей в плоскости рамки и проходящей через ее центр, равны по модулю и одинаково направлены. Суммарный момент сил равен по модулю:

.

По определению модуля магнитного момента (4): IS=p_m, значит, если вектор магнитной индукции лежит в плоскости рамки, то на рамку с током действует механический момент сил , стремящийся повернуть рамку так, чтобы магнитный момент был параллелен вектору .
Схема установки


При включении магнитного поля катушек , направленного перпендикулярно магнитному полю Земли - , магнитная стрелка начинает совершать затухающие колебания около положения устойчивого равновесия. Равновесное положение, в которое стрелка переходит через некоторое время, определяется направлением результирующего вектора магнитной индукции .

Рабочие формулы

формула для определения горизонтальной составляющей вектора магнитной индукции Земли имеет следующий вид:










формула для определения среднего значения угла отклонения магнитной стрелки в прямом и обратном направлении тока



формула для определения среднего значения горизонтальной составляющей вектора магнитной индукции Земли



Погрешность измерения горизонтальной составляющей вектора магнитной индукции Земли



Среднеквадратическая погрешность измерения




Задание 1.

Цель задания 1: Познакомиться со свойствами магнитной стрелки.

Порядок выполнения задания 1а.

1. 
   Убедитесь в том, что установка находится в исходном положении: источник питания выключен, сила тока в катушках равна нулю.
   
2. 
   Приведите установку во вращение.
   

Управлять вращением установки можно кнопками: «влево», «вправо», «стоп», «быстро», «нормально», «медленно».

3. 
   Наблюдайте за поведением стрелки: при вращении установки в разные стороны, после остановки вращения. Результаты наблюдений запишите в отчёт.
   
4. 
   Проанализируйте результаты наблюдений, объясните поведение стрелки.
   
5. 
   Запишите свои выводы в отчёт.
   

Вывод: Магнитная стрелка компаса при отсутствии тока в катушке всегда располагается по магнитному меридиану Земли. Если по ней пропустить ток, то магнитная стрелка повернется на некоторый угол α. Объясняется это тем, что на магнитную стрелку будут действовать два поля: первое – горизонтальная составляющая напряженности поля Земли и второе - созданное током. Под действием этих полей магнитная стрелка займет такое положение равновесия, при котором равнодействующая двух полей будет совпадать с линией, соединяющей полюса стрелки

При вращении установки магнитная стрелка не меняет своего положения, это объясняется тем, что стрелка устанавливается под действием горизонтальной составляющей магнитного поля Земли.

Порядок выполнения задания 1б.

1. 
   При выключенном источнике питания катушек вращая установку, зафиксируйте её в в исходном положении, когда катушки расположены сверху и снизу стрелки.
   
2. 
   Кнопкой «вкл/выкл» включите источник питания. Установите максимальное для данной установки значение силы тока – 3000 мА.
   
3. 
   Поменяйте направление тока в катушках на обратное и наблюдайте за поведением стрелки. Переключите направление тока в катушках на обратное.
   
4. 
   Проанализируйте результаты наблюдений, объясните поведение стрелки.
   
5. 
   Запишите свои выводы в отчёт.
   
6. 
   Не изменяя силу тока в катушках, приведите установку во вращение.
   
7. 
   Объясните поведение стрелки. Запишите свои выводы в отчёт.
   

Вывод: на магнитную стрелку будут действовать два поля: первое – горизонтальная составляющая напряженности поля Земли и второе - созданное током. Под действием этих полей магнитная стрелка займет такое положение равновесия, при котором равнодействующая двух полей будет совпадать с линией, соединяющей полюса стрелки.

Задание 2.

Цель задания 2: Определить горизонтальную составляющую вектора магнитной индукции поля Земли.

Порядок выполнения задания 2.

1. 
   Нарисуйте таблицу результатов измерений и расчётов.
   
2. 
   Запишите в таблицу число витков в катушках N и радиус катушек R.
   
3. 
   При выключенном источнике питания катушек переведите установку в рабочее положение: корпус установки разверните так, чтобы плоскости катушек были параллельны магнитной стрелке.
   
4. 
   Включите источник питания и, увеличивая от нулевого значения силу тока, добейтесь отклонения стрелки на угол, кратный пяти градусам (шкала компаса проградуирована с шагом пять градусов). Отсчёт значения угла следует делать после затухания колебаний стрелки! Результаты измерений силы тока I, угла запишите в таблицу.
   
5. 
   Не изменяя силы тока, измените его направление на обратное. После затухания колебаний стрелки измерьте и запишите в таблицу значение угла.
   
6. 
   Повторить измерения, увеличивая значения силы тока (в данной установке максимальное значение силы тока равно 3000 мА).
   
7. 
   Результаты измерений запишите в таблицу.
   
8. 
   Обработайте результаты измерений
   

Результат измерений

число витков в катушках N= 4 радиус катушек R= 0,056 м
№					Тл	Тл	Тл	Тл
1	30	5	2,5	3,75			-9,2	8,25
2	100	12,5	10	11,25			31,7
3	500	42,5	40	41,25			-1,4
4	1000	60	60	60			-5,7
5	3000	80	77,5	78,75			-15,4

Обработка результатов измерений





















Погрешность измерений





Вывод: в данном задании мы определили горизонтальную составляющую магнитного поля Земли, и получили, что

1. 
   Сформулируйте закон Био-Савара-Лапласа:
   

1. 
   проиллюстрируйте ситуацию рисунком;
   
2. 
   запишите формулу для в векторном виде;
   
3. 
   записать формулу для в скалярном виде.
   

Принцип суперпозиции: поле системы токов равно сумме полей, создаваемых каждым током.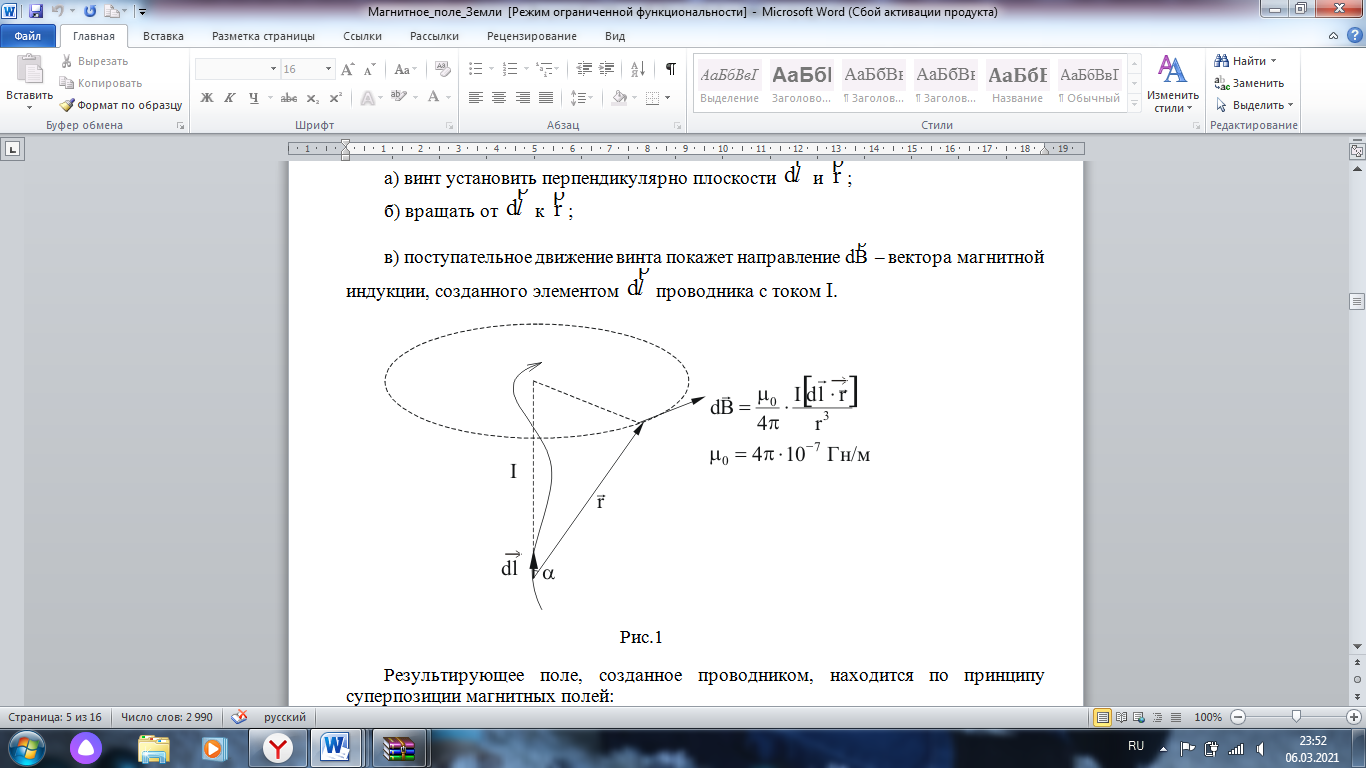

1. 
   Изобразите кольцо радиуса , по которому в заданном направлении те­чет ток силой . Опираясь на закон Био-Савара-Лапласа, выведите форму­лу для индукции магнитного поля в центре кругового тока.
   

Чтобы найти поле в центре кольца с током, мысленно разобьем его на множество элементов тока (см. рис. 2а).



Каждый элемент тока, согласно закону Био-Савара-Лапласа, создает магнитное поле с индукцией, определяемой формулой


Прежде всего проверим, как направлены векторы, создаваемые каждым элементом тока. Пользуясь приведенным выше правилом правого винта для определения направления, легко убедиться, что в центре кольца все векторы направлены в одну сторону, перпендикулярно плоскости кольца. Следовательно, векторную сумму можно заменить арифметической, и для магнитной индукции в центре кольца получаем на основе (2) выражение:



Из геометрии задачи видно, что



Вынося из-под знака интеграла постоянные величины , получаем:



Интеграл по окружности равен ее длине:



Таким образом, магнитная индукция в центре кольца равна:

(3)

Вектор магнитной индукции направлен перпендикулярно плоскости кольца, направление вектора определяется по правилу правого винта для кольцевого тока: винт установить перпендикулярно плоскости кольца и поворачивать по направлению тока в кольце, направление поступательного движения винта покажет направление вектора .

Направление вектора магнитного момента контура с током совпадает с направлением положительной нормали к контуру

3. Изобразите (схематически) исходное положение лабораторной установки в двух состояниях:

а) ток в катушках равен нулю;

б) ток в катушках отличен от нуля;

На каждом рисунке изобразите соответствующие им векторы магнитной ин­дукции.



При включении тока катушки создают магнитное поле, модуль вектора индукции которого определяется следующей формулой:

(9)

При этом устойчивое положение равновесия магнитной стрелки определяется векторной суммой магнитных полей Земли - и катушек -



При включении магнитного поля катушек , направленного перпендикулярно магнитному полю Земли - , магнитная стрелка начинает совершать затухающие колебания около положения устойчивого равновесия. Равновесное положение, в которое стрелка переходит через некоторое время, определяется направлением результирующего вектора магнитной индукции .

В равновесном положении стрелка отклонена от исходного положения на некоторый угол , который можно измерить. Из рисунка 8 видно, что тангенс этого угла:

. (10)

Выражая интересующую нас величину из формулы (10), получим:

. (11)

Подставив из формулы (9) выражение для в формулу (11), получим:

. (12)

Для повышения точности измерений угол отклонения стрелки измеряют два раза, при разных направлениях тока в катушках. Затем находят его среднее значение:

(13)

4.Выведите рабочую формулу для определения горизонтальной составляю­щей вектора магнитной индукции поля Земли.

Рабочая формула для определения горизонтальной составляющей вектора магнитной индукции Земли имеет следующий вид:

.