Лабораторная работа Метод наименьших квадратов Пусть в результате некоторого эксперимента получены данные в виде чисел записанных в таблицу 1 1
 Скачать 0.71 Mb.
|
|
3.4 ЛАБОРАТОРНАЯ РАБОТА «Метод наименьших квадратов» Пусть в результате некоторого эксперимента получены данные в виде чисел записанных в таблицу 3.4.1: Таблица 3.4.1 На основании этих данных требуется установить функциональную зависимость величины  от величины  :  . Вид функции устанавливается обычно или из теоретических соображений или визуально, исследуя расположение  точек  на плоскости  .Наиболее часто в качестве подбираемой функции используют следующие функции: а) полином:  ;б) дробно-рациональную:  ; в) экспоненциальную:  ; (3.4.1)г) логарифмическую и другие функции, где  числа, заранее неизвестные. И задача заключается именно в нахождении этих чисел.Замечание: 1. Если нет никаких теоретических указаний о виде зависимости , то следует искать наиболее простую формулу, содержащую как можно меньшее количество параметров  ;2. Полное совпадение с данными эксперимента и не желательно, т.к. определяемая функция будет повторять ошибки экспериментатора. Существует много различных методов нахождения коэффициентов  . Они излагаются в учебниках по численным методам математики, там же излагаются их достоинства и недостатки. Здесь будет рассмотрен один из этих методов - метод наименьших квадратов.Итак, имеем  функцию многих переменных, которая зависит от и еще нескольких неизвестных величин  .Составим новую функцию    . (3.4.2)Величины надо найти таким образом, чтобы функция  имела наименьшее значение. Иными словами, отклонение экспериментальных точек от теоретической кривой должно быть минимальным.Применяем необходимое условие экстремума функции нескольких переменных:  . (3.4.3) В результате получится система из  линейного уравнения с  м неизвестными . В каждом конкретном случае исследуется вопрос о существовании решения этой системы, единственности этого решения и о наличии минимума функции при полученных значениях величин .Рассмотрим частные случаи подбираемой функции .Пусть  полином 1-й степени, т.е. . График этой функции есть прямая линия. В этом случае вспомогательная функция  есть функция двух переменных и имеет вид: . (3.4.4)Тогда система (3.4.2) будет представлена следующими двумя уравнениями: 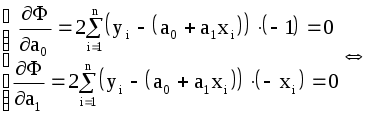 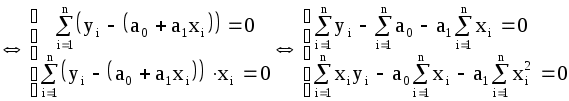 . (3.4.5)Теперь необходимо вычислить коэффициенты системы (значения  и  даны в таблице (3.4.1). Обозначим .Тогда система (3.4.5) принимает вид: 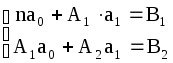 (3.4.6)Эта система из двух линейных уравнений с двумя неизвестными 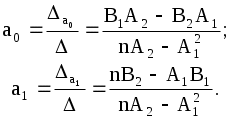 и  . Решим систему по формулам Крамера:  .Если  , то решение существует и оно единственно и это решение:  При найденных значениях и функция (3.4.4) имеет минимальное значение. Это доказывается, если вычислить  при полученных  и подставить в достаточные условия экстремума функции нескольких переменных.ПРИМЕР 3.4.1. На основании некоторого эксперимента получены данные Таблица 3.4.2
Нанесем эти значения на координатную плоскость (рис.3.4.1), визуально исследуем расположение точек. В данном случае можно допустить линейную зависимость величины 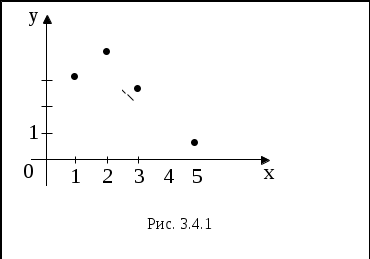 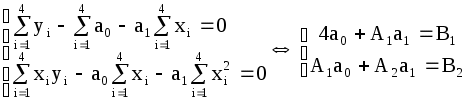от величины , т.е.  . Строим вспомогательную функцию   и тогда система (3.4.5) имеет вид: (3.4.7)Вычислим коэффициенты 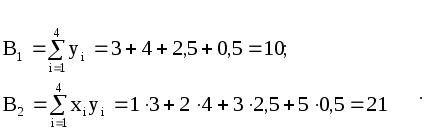 :    Подставим в систему (3.4.7): 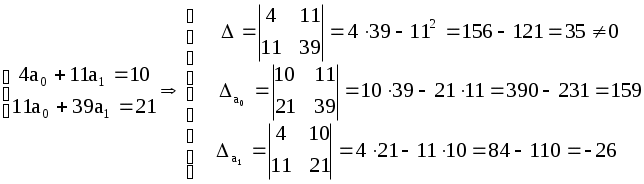 Итак:  В результате получаем функцию  .2. Пусть  полином 2-й степени, т.е.   график этой функции есть парабола. В этом случае вспомогательная функция  есть функция трех переменных и имеет вид: (3.4.8)Тогда система (3.4.3) будет представлена тремя уравнениями: 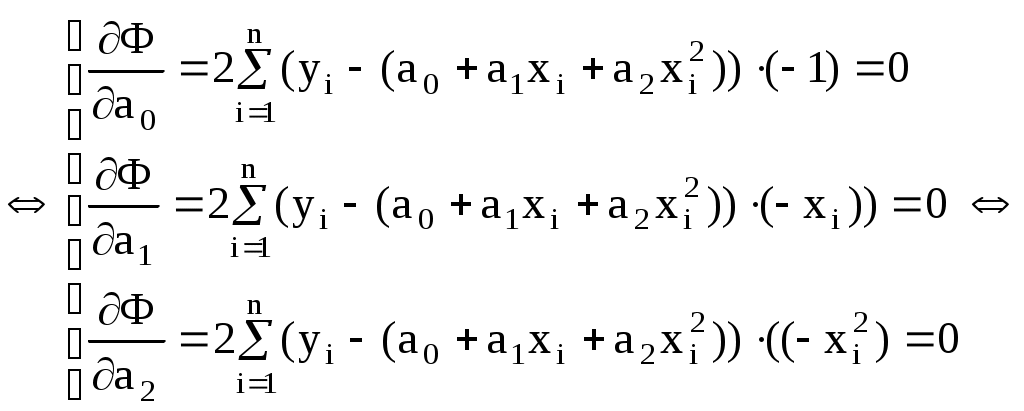 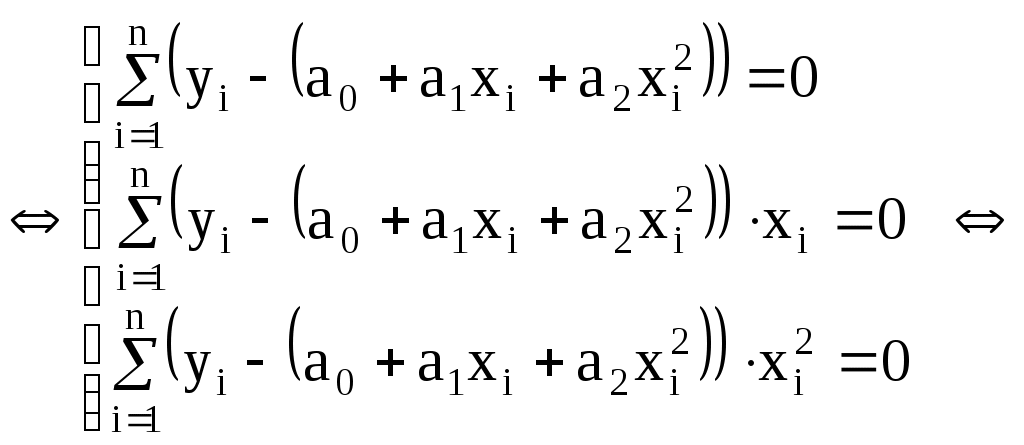 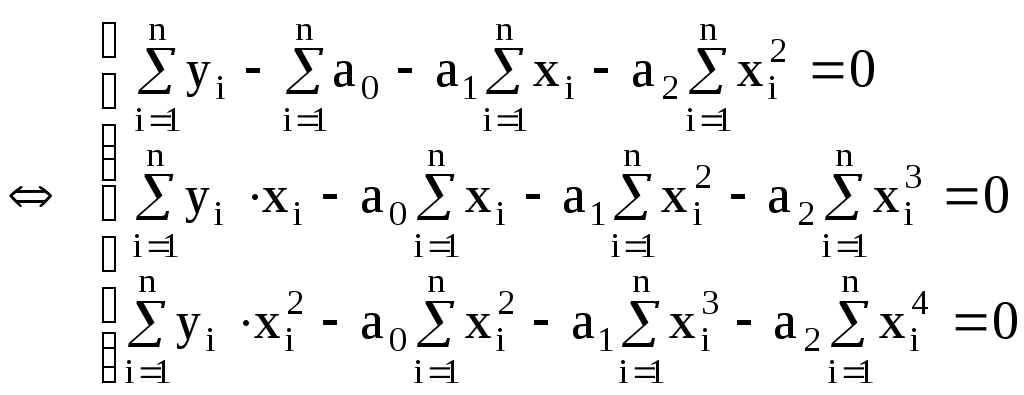 (3.4.9)Теперь необходимо вычислить коэффициенты этой системы (значения 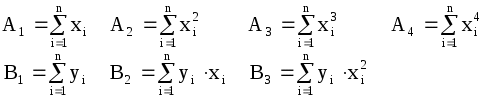и даны в таблице (3.4.1)): С использованием этих чисел система (3.4.9) принимает вид: 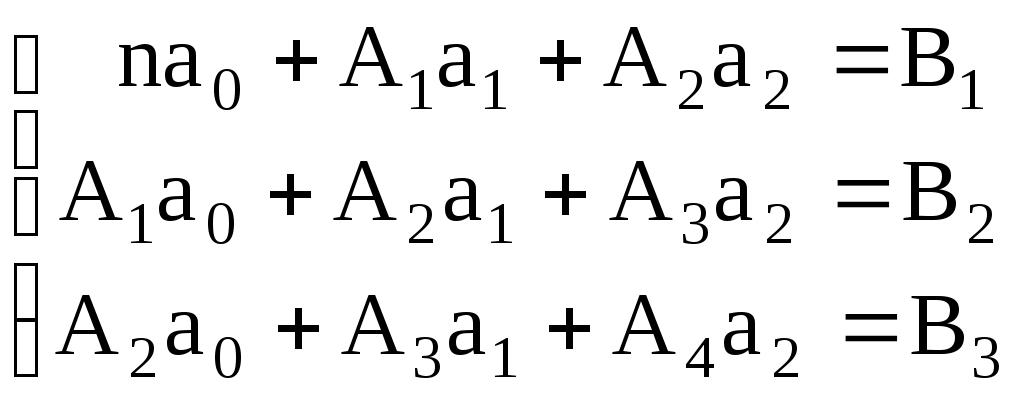 (3.4.10)Эта система из трех линейных уравнений с тремя неизвестными 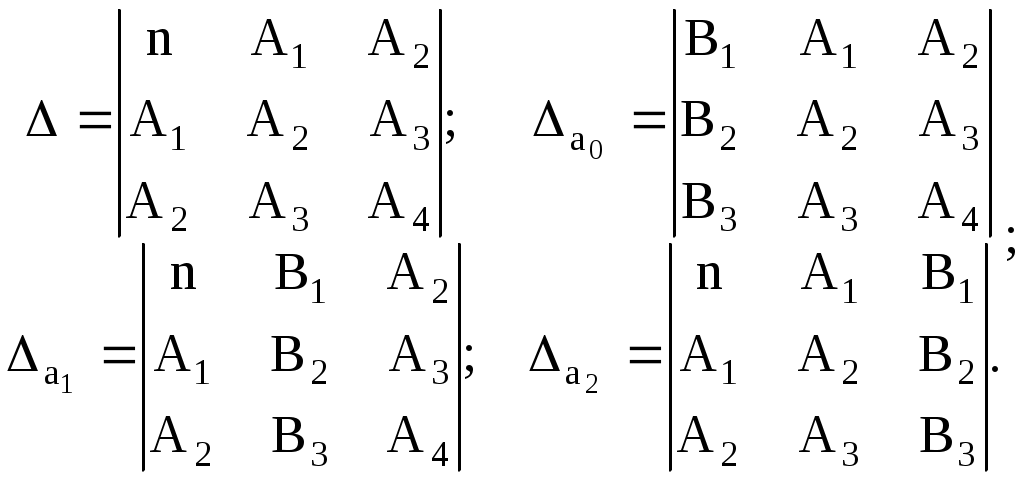 ,  . Решим систему по формулам Крамера: Если , то система (3.4.10) имеет единственное решение: .При найденных значениях , функция (3.4.8) имеет минимальное значение. Это доказывается с использованием достаточных условий экстремума функции нескольких переменных (теорема 1.8).ПРИМЕР 3.4.2. В результате эксперимента получены числовые данные, записанные в виде таблицы 3.4.3: Таблица 3.4.3
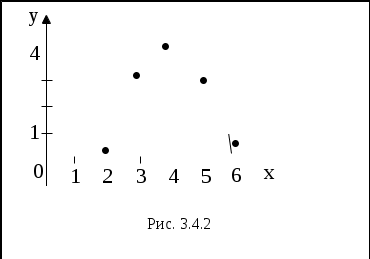 Нанесем эти данные на координатную плоскость, исследуем расположение точек и видим, что зависимость величины 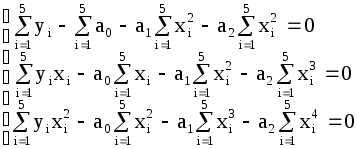от величины можно описать параболой, т.е.  . Строим вспомогательную функцию:  и тогда система (3.4.9) имеет вид: (3.4.11)Теперь необходимо вычислить коэффициенты этой системы:          Подставим полученные значения в систему (3.4.11) или в систему (3.4.10): 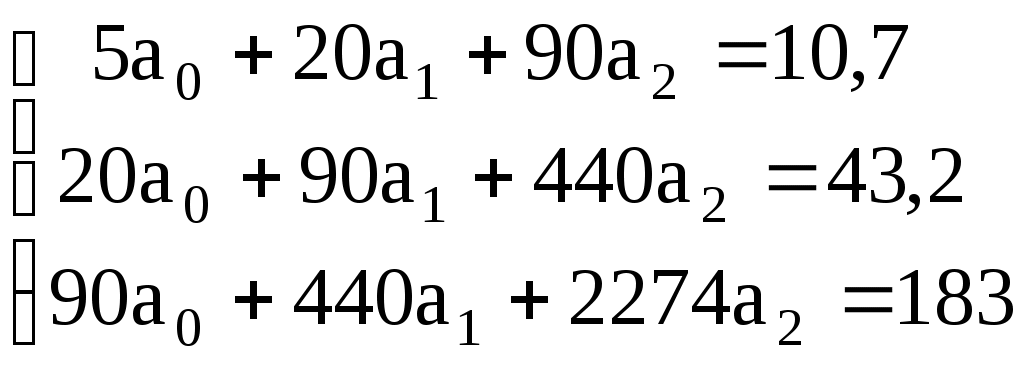 Решаем эту систему линейных уравнений методом Крамера: 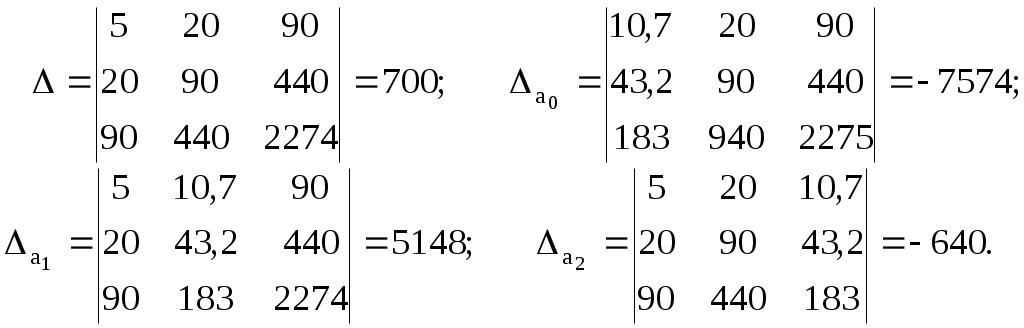  .В результате получаем функцию  .Для анализа полученного уравнения составим таблицу 3.4.4 Таблица 3.4.4
Минимальное значение функции  при найденных коэффициентах равно:  .Если коэффициенты  хотя бы немного изменить, то значение функции будет увеличиваться.3. Пусть экспоненциальная функция, а именно  . В этом случае, при решении системы (3.4.3), возникают трудности, которые, однако, можно преодолеть линеаризацией уравнения  . Логарифмируем его:  . Обозначим  , тогда имеем   это линейное уравнение. Если найдем его коэффициенты, то исходные коэффициенты рассчитаем по формулам  .ПРИМЕР 3.4.3. В результате эксперимента получены данные, выписанные в виде таблицы 3.4.5: Таблица 3.4.5
Нанесем эти данные на координатную плоскость (рис.3.4.3), исследуем расположение точек и видим, что лучше всего зависимость в  еличины от величины описывается экспоненциальной функцией: . Поскольку в данном случае  , то прологарифмируем уравнение:  , сделаем обозначения  ;  ;  и получаем линейное уравнение  . (3.4.12)Для нахождения коэффициентов у последнего уравнения, воспользуемся изложенной выше теорией и обратимся к примеру 3.4.1. Таблица 3.5.6
Строим вспомогательную функцию 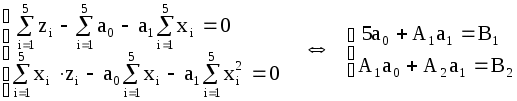 . Система (3.4.5) имеет вид в этом случае: (3.4.13)Вычислим коэффициенты :     .Подставим в систему (3.4.13): 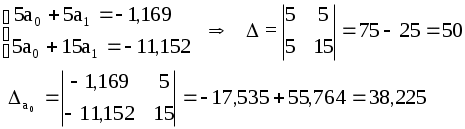   ,  . Возвращаемся к коэффициентам  и  . Так как  , то найдем искомые коэффициенты:  , а также получим функцию  .Для анализа полученного уравнения составим таблицу 3.4.7: Таблица 3.4.7
Минимальное значение функции при найденных коэффициентах равно: |
