|
Лекция 19 Семь инструментов контроля.
19.1. Диаграмма разброса (рассеивания)
Японский союз ученых и инженеров в 1979 г. включил диаграмму разброса в состав семи методов контроля качества.
Существующие названия – Диаграмма разброса, диаграмма рассеяния, поле корреляции
Применяется в производстве и на различных стадиях жизненного цикла продукции для выяснения зависимости между показателями качества и основными факторами производства.
Цель - выяснение существования зависимости и выявление характера связи между двумя различными параметрами процесса.
Суть - диаграмма разброса (поле корреляции) - инструмент, позволяющий определить вид и тесноту связи между парами соответствующих переменных.
Эти две переменные могут относиться к:
а) характеристике качества и влияющему на нее фактору;
б) двум различным характеристикам качества;
в) двум факторам, влияющим на одну характеристику качества.
Результат - принятие решения о проведении необходимых мероприятий на основании анализа диаграммы разброса.
Достоинства - наглядность, и простота оценки связей между двумя переменными.
Недостатки - к оценке диаграммы следует привлекать тех, кто владеет информацией о продукции, чтобы исключить неправильное использование этого инструмента.
Диаграмма разброса -это точечная диаграмма в виде графика, получаемого путем нанесения в определенном масштабе экспериментальных, полученных в результате наблюдений, точек. Координаты точек на графике соответствуют значениям рассматриваемой величины и влияющего на него фактора. Расположение точек показывает наличие и характер связи между двумя переменными (например, скорость и расход бензина, или выработанные часы и выход продукции).
По полученным экспериментальным точкам могут быть определены и числовые характеристики связи между рассматриваемыми случайными величинами: коэффициент корреляции и коэффициенты регрессии.
Построение диаграммы разброса выполняется в следующей последовательности.
Этап 1. Соберите парные данные (х, у) в таблицу. Не менее 25-30 пар данных.
Этап 2. Найдите хмакс , хмин и умакс , умин. Для фактора горизонтальная ось х, а для характеристики качества - вертикальная ось у, длины рабочих частей - приблизительно одинаковые, на каждой оси от 3 до 10 градаций. Если разброс значений изучаемого параметра качества составляет несколько порядков, то удобно применять логарифмический масштаб по обеим осям.
Этап 3. При нанесении данных таблицы на график одинаковые значения - концентрические кружки (Θ), или наносят вторую точку рядом с первой.
Этап 4. Идентификация: название диаграммы; интервал времени; число пар данных; названия и единицы измерения для каждой оси; имя (и прочее) человека, который делал эту диаграмму, дата составления графика и т.д.
При регистрации данных во время измерений приводят сопровождающую информацию: цель, наименование объекта измерения, название процесса характеристики, способ выборки, дата, время измерения, температура, влажность, метод измерения, тип измерительного прибора, имя оператора, проводившего измерения (для данной выборки), и др.
|
Применение диаграммы разброса для анализа причинно-следственной диаграммы заключается в наблюдении характера изменения параметров качества во времени при воздействии факторов.
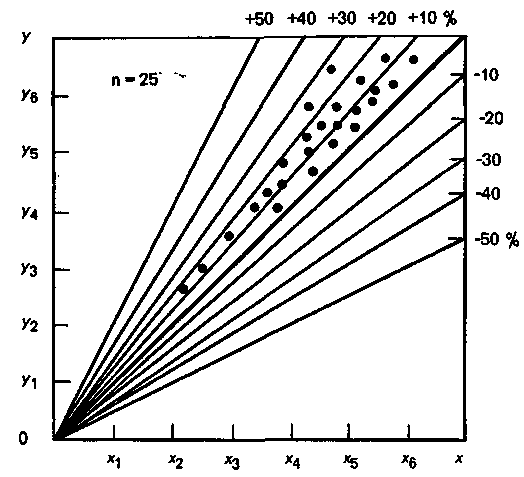
Рис. 1. Диаграмма разброса
|
Например, исследуется влияние определенных факторов (например, температуры, влажности) на обратный ток p-n-перехода однотипных полупроводниковых структур (Iобр)
1. По оси абсцисс откладывают начальные значения изучаемого параметра качества, в результате будем иметь упорядоченный ряд значений х1, х2, х3,..., хn параметра качества полупроводниковых структур в момент времени t = 0, которые наносят на ось абсцисс.
2. На ось ординат наносят замеренные значения параметра качества у тех же самых полупроводниковых структур по окончании эксперимента - ряд значений параметра качества через время t = ti, в виде упорядоченного ряда у1, у2,..., уn,
3. Значение параметра качества каждого изделия до и после эксперимента будет обозначаться точкой в системе указанных координат. Все n изделий, подвергшихся эксперименту, будут изображаться разбросанными по координатному полю точками. Эта совокупность точек образует диаграмму разброса (поле корреляции) (рис. 1).
4. Анализ диаграммы разброса позволяет наглядно показать характер изменения параметра качества во времени.
|
Анализ диаграммы разброса для
выявления характера изменения параметра качества во времени.
Проведем из начала координат биссектрису.
Все точки легли на биссектрису - значения данного параметра не изменились в процессе эксперимента. Рассматриваемый фактор (или факторы) не влияет на параметр качества.
Основная масса точек лежит под биссектрисой - значения параметра качества за прошедшее время уменьшились.
Точки ложатся выше биссектрисы - значения параметра за рассматриваемое время возросли.
Проведя лучи из начала координат, соответствующие уменьшению и увеличению параметра на 10, 20, 30, 50 %, можно путем подсчета точек между прямыми выяснить частоту значений параметра в интервалах 0...10 %, 10...20 % и т.д.
Анализ диаграммы разброса для определения вида связей.
Данное применение наиболее распространено.
Точно так же, как по гистограмме, можно распознать форму распределения, по диаграмме рассеивания можно представить себе общее распределение пар.
1. Выясняем, есть ли на диаграмме какие-нибудь далеко отстоящие точки (выбросы). Из предположения, что любые такие точки, удаленные от основной группы, либо результат ошибок измерения или записи данных, либо обусловлены некоторыми изменениями в условиях работы эти точки надо исключаются из корреляционного анализа.
2. Существуют специальные критерии, позволяющие объективно оценить принадлежность подозрительных точек (экспериментальных значений) к той генеральной совокупности, из которой они взяты, и выявить среди них "чужеродные" точки. Пренебрегая этими точками, следует обратить внимание на причины таких нерегулярностей, поскольку, отыскивая их причины, мы часто оказываемся вознагражденными неожиданной, но весьма полезной информацией.
Возможные многочисленные варианты скоплений точек и некоторые типичные из них приведены на рис. 2-8.
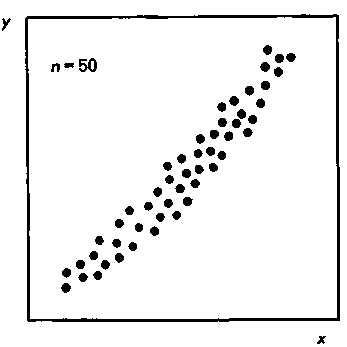
Рис. 2. Прямая корреляция
|
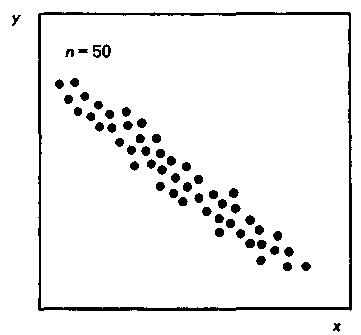
Рис. 4. Обратная (отрицательная) корреляция
|
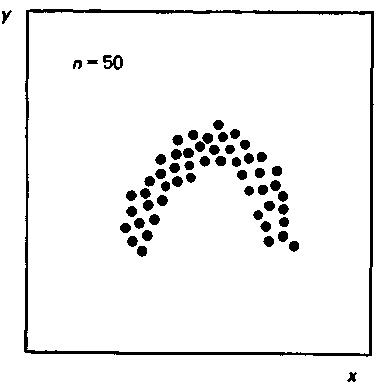
Рис. 6. Криволинейная корреляция
|
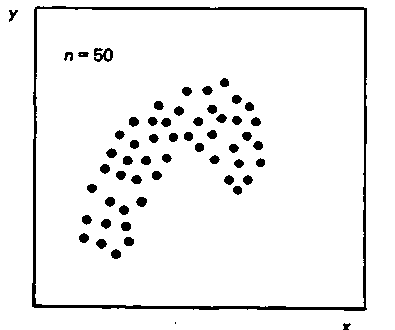
Рис. 7. Легкая криволинейная корреляция
|
При осуществлении контроля за причинным фактором х можно управлять значением параметра качества у.
|
Если при криволинейной корреляции диаграмму разброса можно разделить на участки, имеющие прямолинейный характер, то проводят такое разделение и исследуют каждый участок в отдельности, как прямолинейную корреляцию.
|
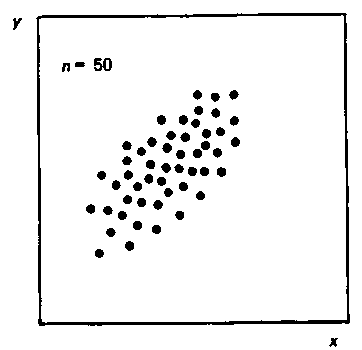
Рис. 3. Легкая прямая корреляция
|
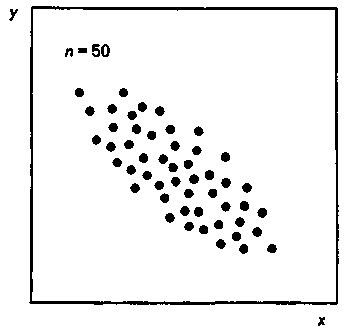
Рис. 5. Легкая обратная "корреляция
|
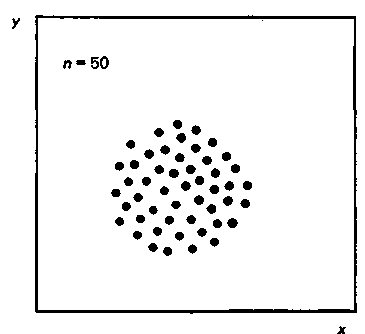
Рис. 8. Отсутствие корреляции
|
В этом случае необходимо продолжить поиск факторов, коррелирующих с у, исключив из этого поиска фактор х.
|
С помощью контроля причинного фактора х можно до некоторой степени держать под контролем характеристику у, но необходимо также иметь в виду и другие факторы, оказывающие влияние на у.
|
|
|
Метод медиан.
При анализе и контроле процесса приходится встречаться с разными характеристиками положения – средним значением, медианой и модой случайной величины.
Если полученные при измерениях значения расположить в возрастающем или убывающем порядке, то медианой будет значение Me, занимающее серединное значение в ряду. Таким образом, медиана — это значение параметра, которое делит упорядоченный ряд на две равные по объему группы. При нечетном числе измерений, т.е. при n = 2i+1, значение параметра для случая i+1 будет медианным. При четном числе измерений (2i) медианой является средняя арифметическая двух значений, расположенных в середине ряда.
Таким образом, формулы для вычисления медианы имеют следующий вид:
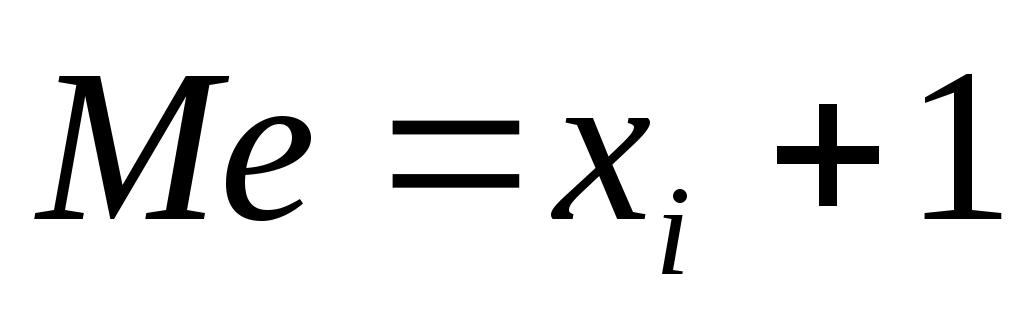 (1) (1)
|
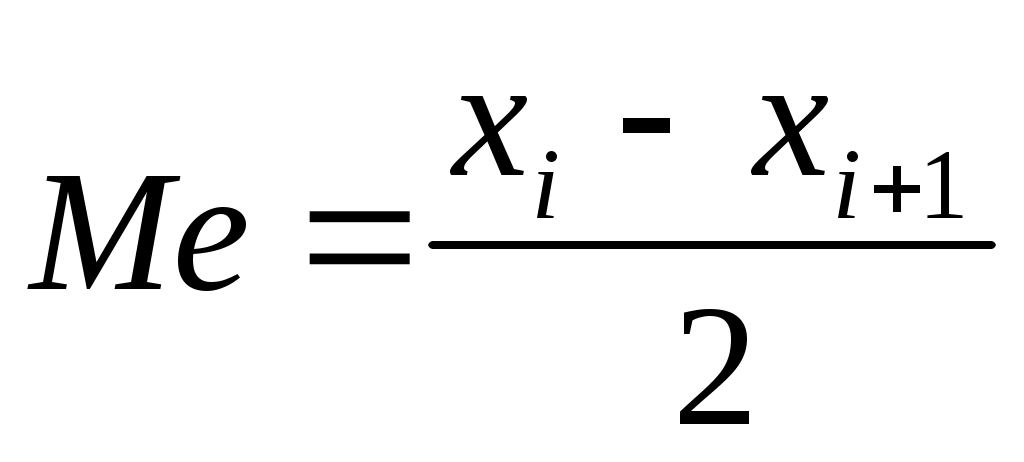 (2) (2)
|
для нечетного числа измерений;
|
для четного числа измерений.
|
Последовательность применения метода медиан
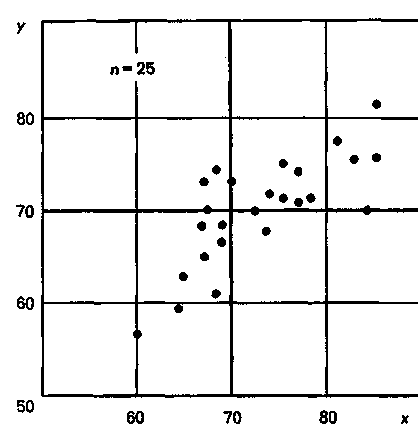
Рис. 11. Диаграмма разброса для
обратного тока р-n-перехода
|
На диаграмме разброса проводятся вертикальная и горизонтальная линии медиан (рис. 11). Выше и ниже горизонтальной медианы, справа и слева от вертикальной медианы будет равное число точек. Если число точек окажется нечетным, следует провести линию через центральную точку.
В каждом из четырех квадратов, получившихся в результате разделения диаграммы разброса вертикальной и горизонтальной медианами, подсчитывают число точек и обозначают их n1, n2, n3 и n4 соответственно. Точки, через которые прошла медиана, не учитывают.
3. Отдельно складывают точки в положительных и отрицательных квадратах:
n(+) = n1 + n3 = 10 + 8 = 18,
n (-) = n2 + n4 = 1 + 2 = 3,
n' = n(+) + n (-) = 18 + 3 = 21.
Так как четыре точки находятся на медианах, то n' не равно n = 25.
|
Таблица 1. Таблица кодовых значений
n′
|
β
|
n′
|
β
|
n′
|
β
|
n′
|
β
|
0,01
|
0,05
|
0,01
|
0,05
|
0,01
|
0,05
|
0,01
|
0,05
|
8
|
0
|
0
|
|
|
|
|
|
|
|
|
|
9
|
0
|
1
|
|
|
|
|
|
|
|
|
|
10
|
0
|
1
|
|
|
|
|
|
|
|
|
|
11
|
0
|
1
|
31
|
7
|
9
|
51
|
15
|
18
|
71
|
24
|
26
|
12
|
1
|
2
|
32
|
8
|
9
|
52
|
16
|
18
|
72
|
24
|
27
|
13
|
1
|
2
|
33
|
8
|
10
|
53
|
16
|
18
|
73
|
25
|
27
|
14
|
1
|
2
|
34
|
9
|
10
|
54
|
17
|
19
|
74
|
25
|
28
|
15
|
2
|
3
|
35
|
9
|
11
|
55
|
17
|
19
|
75
|
25
|
28
|
16
|
2
|
3
|
36
|
9
|
11
|
56
|
17
|
20
|
76
|
26
|
28
|
17
|
2
|
4
|
37
|
10
|
12
|
67
|
18
|
20
|
77
|
26
|
29
|
18
|
3
|
4
|
38
|
10
|
12
|
68
|
18
|
21
|
78
|
27
|
29
|
19
|
3
|
4
|
39
|
10
|
12
|
69
|
19
|
21
|
79
|
27
|
30
|
20
|
3
|
5
|
40
|
11
|
13
|
60
|
19
|
21
|
80
|
28
|
30
|
21
|
4
|
5
|
41
|
11
|
13
|
61
|
20
|
22
|
81
|
28
|
31
|
22
|
4
|
5
|
42
|
12
|
14
|
62
|
20
|
22
|
82
|
28
|
31
|
23
|
4
|
6
|
43
|
12
|
14
|
63
|
20
|
23
|
83
|
29
|
32
|
24
|
5
|
6
|
44
|
13
|
15
|
64
|
21
|
23
|
84
|
29
|
32
|
25
|
5
|
7
|
45
|
13
|
15
|
65
|
21
|
24
|
85
|
30
|
32
|
26
|
6
|
7
|
46
|
13
|
15
|
66
|
22
|
24
|
86
|
30
|
33
|
27
|
6
|
7
|
47
|
14
|
16
|
67
|
22
|
25
|
87
|
31
|
33
|
28
|
6
|
8
|
48
|
14
|
16
|
68
|
22
|
25
|
88
|
31
|
34
|
29
|
7
|
8
|
49
|
15
|
17
|
69
|
23
|
25
|
89
|
31
|
34
|
30
|
7
|
9
|
50
|
15
|
17
|
70
|
23
|
26
|
90
|
32
|
35
|
|
4. Для определения наличия и степени корреляции по методу медиан используется специальная таблица (табл. 1) кодовых значений, соответствующих различным n' при двух значениях коэффициента риска - β (0,01 и 0,05).
Сравнивая меньшее из чисел n(+) и n (-) с их кодовым значением из табл. 1, соответствующим значению n', делают заключение о наличии и характере корреляции. Если меньшее из чисел n(+) и n (-) оказывается равным или меньше табличного кодового значения, то корреляционная зависимость имеет место.
Если подсчитанные значения окажутся больше соответствующего кодового значения, то это означает отсутствие прямолинейной корреляции, однако это не значит, что не может быть криволинейной корреляционной зависимости. Для выяснения этого вопроса необходимо проводить регрессионный и корреляционный анализы.
Это утверждение делается с вероятностью ошибиться только в одном случае из ста (β = 0,01). В этом и заключается смысл числового значения коэффициента риска β. Поскольку n(+) > n (-) это свидетельствует о прямой корреляции. В тех случаях, когда n(+) < n (-) , можно говорить об обратной корреляции.
|
В рассматриваемом примере табличное кодовое значение при коэффициенте риска β = 0,01, соответствующее n' = 21, равно 4. Меньшим из чисел n(+) = 18 и n (-) = 3 является n (-). Поскольку n (-) равное 3, оказывается меньше кодового значения 4, можно утверждать, что в данном случае между двумя параметрами существует прямолинейная корреляционная зависимость.
|
Временной лаг взаимосвязи переменных.
Путем сдвига во времени значений одного параметра относительно соответствующих значений другого рассматриваемого параметра можно получить более конкретную информацию о воздействующих факторах.
При построении диаграммы разброса в исходных таблицах значения х (x1, x2,..., хn) соответствуют значениям у (y1, y2,...,yn). При этом мы рассматриваем точки, соответствующие (x1, y1), (x2,y2) ..,(xn,yn).
А что, если это соответствие, например, сместить на один месяц, т.е. рассматривать соответствующие этому случаю следующие парные значения: (x1, у2), (х2, y3),..., (x11, у12). Тогда диаграмма разброса будет иметь вид, приведенный на рис. 12.
Подобный временной сдвиг называют временным лагом. Таким образом, диаграмма рис. 12 — это диаграмма разброса с временным лагом в один месяц. Если задать временной лаг в два и три месяца, то получим соответственно диаграммы рис. 13 и 14.
Из сравнения диаграмм видно, что наивысшая корреляция достигается при временном лаге в два месяца (на рис.13. точки группируются более явно около прямой, чем на рис. 14). Иными словами, рекламации на продукцию В хорошо коррелируют с рекламациями на продукт А, пришедшими за два месяца до них. Именно в это время нужно выявлять факторы, влияющие на качество продукта.
 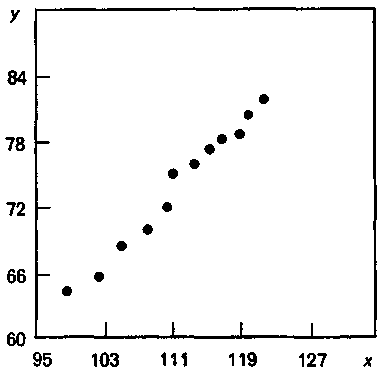 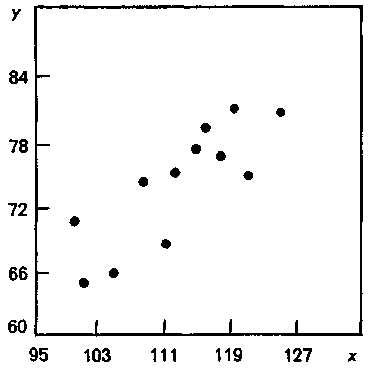
Рис. 12. Диаграмма разброса Рис. 13. Диаграмма разброса Рис. 14. Диаграмма разброса с с лагом в один месяц с лагом в два месяца с лагом в три месяца
При временном лаге может возникнуть проблема определения числа рекламаций в будущем. Так, для временного лага в два месяца необходимо определить число рекламаций у13 на продукт В в 13-м месяце. Для этого используют прямую регрессии и соответствующую ей формулу
 (3) (3)
где s(x) и s(y) - выборочное стандартное отклонение соответственно для значений х и у, а г - коэффициент корреляции
Выборочное стандартное отклонение для простой статистической совокупности при наличии частот определяется соответственно по следующей формуле:
 ; ;  (4) (4)
откуда
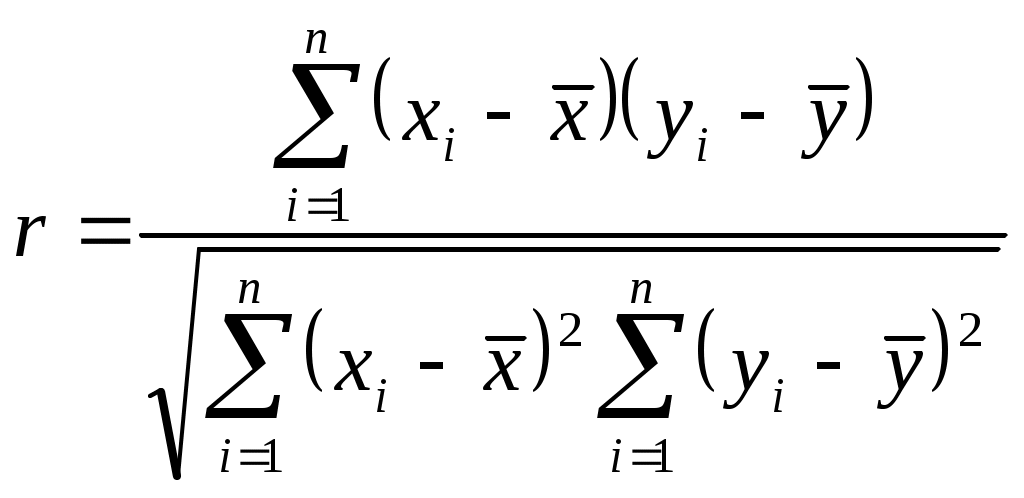 (5) (5)
Тогда, если вычислить  , , 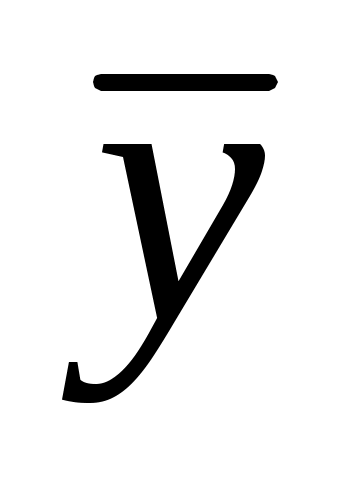 , s(x), s(y) и г, можно найти предсказанные значения (прогноз) у для заданного значения х. , s(x), s(y) и г, можно найти предсказанные значения (прогноз) у для заданного значения х.
Попробуем предсказать значения у13 числа рекламаций на продукт В в 13-м месяце при временном лаге в два месяца, пользуясь данными табл. 3.10.
Коэффициент корреляции при временном лаге в два месяца в соответствии с формулой (5) составляет г = 0,99, а средние и стандартные отклонения примут следующие значения:
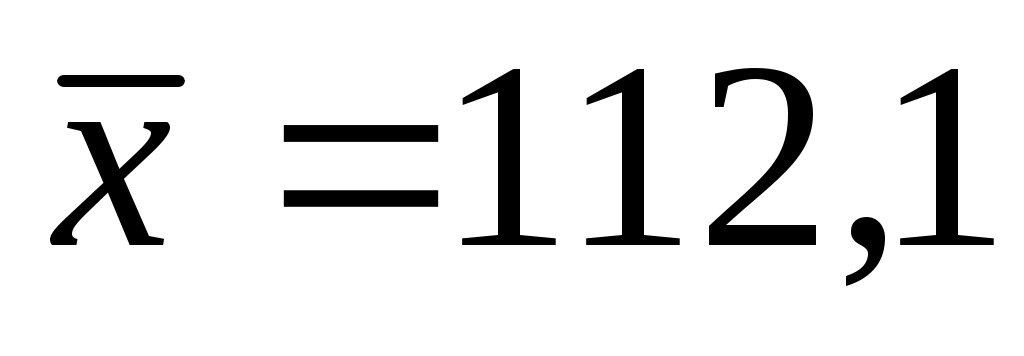 ; s(x)=7,76 ; s(x)=7,76
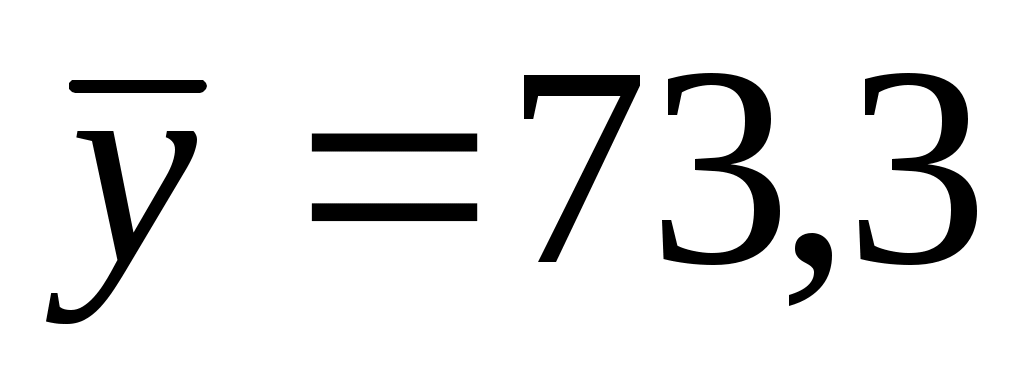 ; s(y)=5,51. ; s(y)=5,51.
По формуле прямой регрессии (3) получаем
у - 73,7 = 0,99 (5,51/7,76)(х - 112,1).
Тогда значение у13 для продукта В (за 13-й месяц) при х11 = 125 составит у13 = 82,8.
Разъяснение недостатков
Так же как и любой другой из инструментов SPS (статистического управления процессами) диаграмма рассеяния - это очень мощное оружие, которое, однако, может быть неправильно использовано. Диаграмма может быть оценена теми, кто много знает о продукции или о процессе, например, операторами, инженерами, контролерами и обслуживающим персоналом.
|
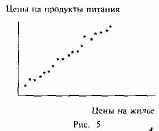
1.Если две переменные кажутся связанными, это не означает, что они таковыми являются. Возможно, существуют и другие причины того, что две переменные кажутся связанными. (рис 5)
2. Только существование очевидной графической связи между двумя переменными еще не означает, что изменение одной из них приводит к изменению другой. Например, подобная диаграмма связывает значения индекса Доу Джонса с глубиной озера Верхнее с 1925 по 1965 гг. Очевидно, что эти величины не связаны между собой, хотя это гораздо труднее заметить.
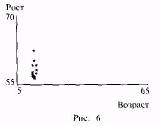
3. Если данные не кажутся связанными, это не означает, что они не связаны. Для этого может существовать множество причин: приведены данные для слишком малого числа лиц, для получения данных были использованы разные объекты, большая погрешность в измерениях.
|
Кажется, что цена продуктов питания и стоимость жилья связаны друг с другом, но на деле обе эти величины связаны с инфляцией или с ростом стоимости производства.
|
|

|

|
Приведены данные для слишком малого числа лиц; следовало найти детей и в других классах школы.
|
Для получения данных использована более чем одна модель автомобиля. Следовало бы построить несколько диаграмм, по одной для каждого типа автомобилей, использованных в исследовании.
|
Большая ошибка в измерениях скрывает наличие связи.
| |
 Скачать 171.5 Kb.
Скачать 171.5 Kb.


 ;
;  (4)
(4)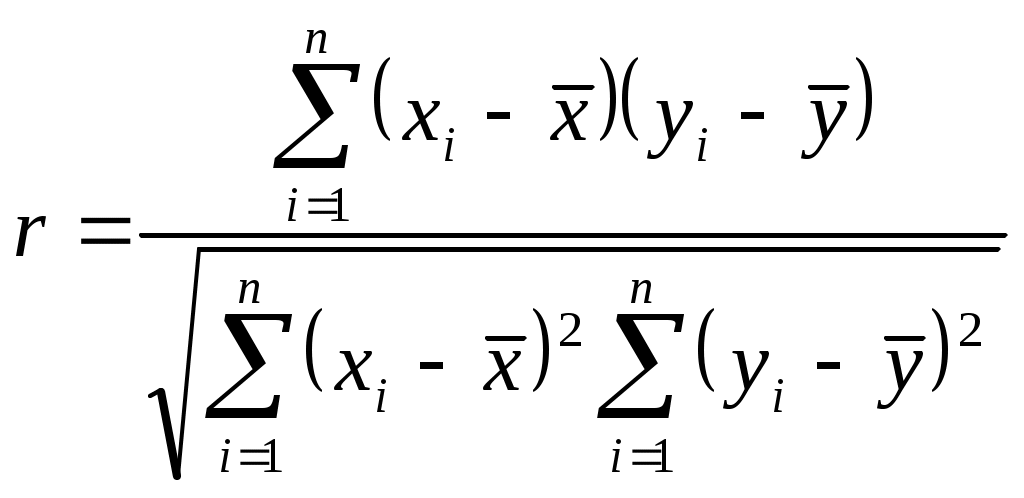 (5)
(5)












