Са. Лекции 3-4. Лекция 3 Касательная плоскость и нормаль к поверхности. Производная по направлению. Градиент функции
 Скачать 245.01 Kb. Скачать 245.01 Kb.
|
|
ЛЕКЦИЯ 3 Касательная плоскость и нормаль к поверхности. Производная по направлению. Градиент функции. цель лекции: ввести понятие касательной плоскости и нормали к поверхности, производной по направлению и градиента; рассмотреть примеры составления уравнений касательной плоскости и нормали к поверхности ключевые слова (термины): касательная плоскость, нормаль к поверхности, производная по направлению, градиент основные вопросы (положения) и краткое содержание: Касательная плоскость и нормаль к поверхности. Пусть имеем поверхность, заданную уравнением вида: 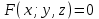 (1.24) (1.24) Прямая линия называется касательной к поверхности в некоторой точке  , если она является касательной к какой-либо кривой, лежащей на поверхности и проходящей через точку , если она является касательной к какой-либо кривой, лежащей на поверхности и проходящей через точку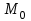 . . Все касательные прямые к поверхности (1.24) в точке 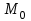 лежат в одной плоскости. Эту плоскость называют касательной плоскостью. Прямая проведенная через точку лежат в одной плоскости. Эту плоскость называют касательной плоскостью. Прямая проведенная через точку поверхности (1.24) перпендикулярно касательной плоскости, называется нормалью к этой плоскости. поверхности (1.24) перпендикулярно касательной плоскости, называется нормалью к этой плоскости.Приведем уравнения касательной плоскости и нормали к поверхности 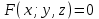 в точке в точке без вывода: без вывода:Ур-е касательной плоскости:  (1.25) (1.25)уравнение нормали: 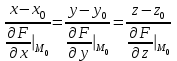 (1.26) (1.26)Если уравнение поверхности задано в форме  или или  , то уравнения (1.25) и (1.26) примут вид соответственно: , то уравнения (1.25) и (1.26) примут вид соответственно: (1.27) (1.27) 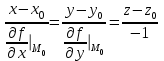 (1.28) (1.28)Пример. Написать уравнение касательной плоскости и уравнение нормали к поверхности шара 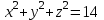 в точке в точке  . .Решение. 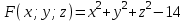 , , 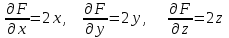 при  имеем имеем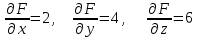 . . Следовательно, уравнение касательной плоскости будет иметь вид 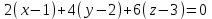 или или 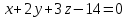 Уравнение нормали: 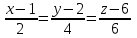 или или 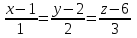 . .Производная по направлению. Градиент Пусть функция  непрерывна в некоторой области D, и точке непрерывна в некоторой области D, и точке 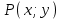 из этой области соответствует на поверхности из этой области соответствует на поверхности  точка точка 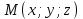 , а точке , а точке 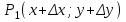 соответствует точка соответствует точка 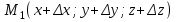 . .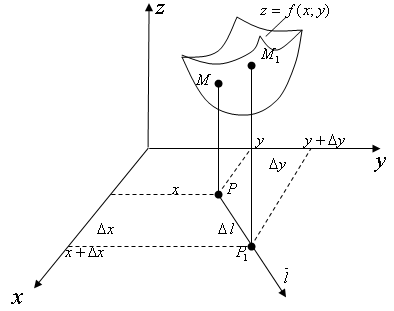 Обозначим направление вектора  через через 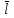 ,а углы, которые он образует осями координат через ,а углы, которые он образует осями координат через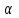 и и  . При перемещении точки . При перемещении точки 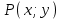 по направлению вектора по направлению вектора 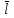 на величину на величину 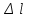 получается приращение получается приращение  . .Отношение  выражает среднюю скорость изменения функции выражает среднюю скорость изменения функции  в направлении в направлении 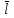 на участке на участке 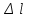 , а предел этого отношения при , а предел этого отношения при 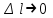 выражает мгновенную скорость изменения функции z в точке Р в направлении выражает мгновенную скорость изменения функции z в точке Р в направлении 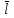 . .Производной функции двух переменных  в данном направлении в данном направлении 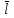 называется предел отношения называется предел отношения  при условии, что при условии, что 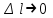 , то есть , то есть 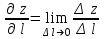 . .Если функция  дифференцируема в точке дифференцируема в точке 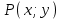 , то её полное приращение в этой точке можно записать так: , то её полное приращение в этой точке можно записать так: 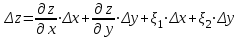 ,где ,где  - бесконечно малые функции при - бесконечно малые функции при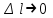 . .Так как  , то , то 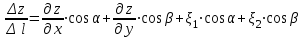 . .Переходя к пределу при 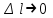 , получим формулу для вычисления производной по направлению , получим формулу для вычисления производной по направлению  (1.32) (1.32)В случае функции трех переменных 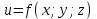 формула для вычисления производной по направлению примет вид: формула для вычисления производной по направлению примет вид: 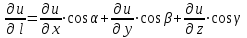 (1.33) (1.33)Пример 1. Найти производную функции 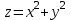 в направлении в направлении 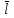 , составляющем с положительным направлением оси Ох угол , составляющем с положительным направлением оси Ох угол 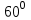 . .Решение.Найдем частные производные  . .Так как 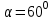 , то , то 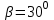 . Тогда . Тогда 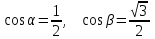 . .Подставляя все выражения в (7.32), получим: 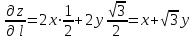 . .Пример 2.Дана функция 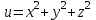 . Найти производную этой функции в точке . Найти производную этой функции в точке 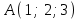 в направлении вектора в направлении вектора  , где , где  . .Решение.Найдем сначала координаты вектора  : : . .Вычисляем направляющие косинусы полученного вектора:  . .Частные производные исходной функции в точке А равны: 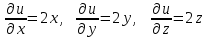 , , 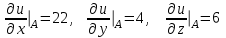 . .Подставляя все найденные значения в формулу(7.33), будем иметь: 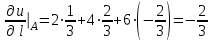 . .Градиентом функции 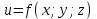 называется вектор, координатами которого являются значения частных производных функции называется вектор, координатами которого являются значения частных производных функции 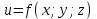 в точке в точке 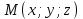 , и обозначается , и обозначается  . .Теперь правую часть формулы (1.33) можно представить в виде скалярного произведения единичного вектора 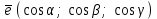 на на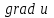 : :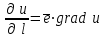 или или 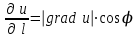 , ,где 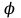 - угол между вектором - угол между вектором 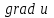 и направлением и направлением 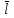 . .Из последней формулы следует, что производная по направлению достигает наибольшего значения , когда 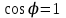 , т.е при , т.е при  . Значит, направление градиента совпадает с направлением . Значит, направление градиента совпадает с направлением 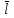 , вдоль которого функция меняется быстрее всего, т.еградиент функции указывает направление наибыстрейшего возрастания функции. , вдоль которого функция меняется быстрее всего, т.еградиент функции указывает направление наибыстрейшего возрастания функции.Наибольшая скорость изменения функции 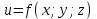 в точке в точке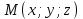 равна: равна: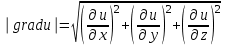 . .В этом заключается физический смысл градиента. Пример 1. Вычислить градиент функции 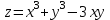 в точке в точке  . .Решение. Вычислим значения частных производных данной функции в точке  : : 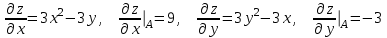 .Значит, градиент будет равен: .Значит, градиент будет равен: 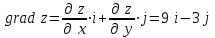 . .Вопросы для самоконтроля: 1.Что называется касательной плоскостью? нормалью к поверхности? 2. Дать определение производной по направлению, градиента. критерии оценки достижения обучающимися результатов обучения: Даны в силлабусе. рекомендуемая литература: Дана в силлабусе. ЛЕКЦИЯ 4 Экстремум функции двух переменных. Нахождение наибольшего и наименьшего значения функции в заданной области цель лекции: ввести понятие экстремума функции двух переменных; рассмотреть примеры нахождения наибольшего и наименьшего значения функции в заданной области ключевые слова (термины): экстремум, наибольшее и наименьшее значение основные вопросы (положения) и краткое содержание: Необходимые условия существования экстремума. Говорят, что функция  имеет в точке имеет в точке максимум, если в окрестности этой точки выполняется неравенство: максимум, если в окрестности этой точки выполняется неравенство:  Говорят, что функция  имеет в точке имеет в точке максимум, если в окрестности этой точки выполнится неравенство: максимум, если в окрестности этой точки выполнится неравенство:  Теорема. Если функция  имеет в точке имеет в точке  экстремум и в этой точке существуют частные производные экстремум и в этой точке существуют частные производные 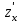 и и  , то в этой точке: , то в этой точке:  , , 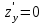 . .Точки, в которых частные производные функции  равны нулю называютсякритическими или стационарными точками функции. равны нулю называютсякритическими или стационарными точками функции.Приведенные условия существования экстремума не являются достаточными, о чем свидетельствует следующий пример 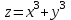 , , 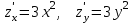 . .Частные производные равны нулю в точке (0;0), но функция в этой точке экстремума не имеет, так как в окрестности этой точки функция принимает значения разных знаков, а в самой точке 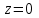 . .Т.е. для нахождения экстремума функции двух переменных необходимо каждую критическую точку подвергнуть дополнительному исследованию. Достаточные условия существования экстремума. Пусть в некоторой области, содержащей точку  функция функция  имеет непрерывны частные производные до третьего порядка включительно. Пусть, кроме того, точка имеет непрерывны частные производные до третьего порядка включительно. Пусть, кроме того, точка  является критической точкой функции является критической точкой функции  , т.е. , т.е.  . .Тогда при 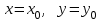 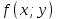 имеет максимум, если: имеет максимум, если: 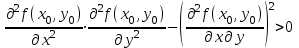 и и 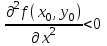 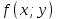 имеет минимум, если имеет минимум, если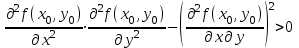 и и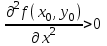 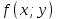 не имеет экстремума, если не имеет экстремума, если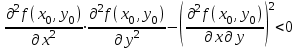 . .Пример. Исследовать на экстремум функцию: 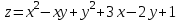 . .Решение: Найдем критические точки: 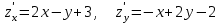 Приравнивая эти функции к нулю и решая полученнуюсистемууравнений: 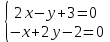 Находим: Находим: 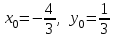 . .Т.е. мы получили одну критическую точку 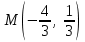 . .Далее находим частные производные второго порядка: 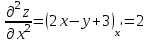 , , 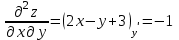 , , 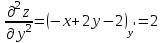 На основании достаточного условия существования экстремума определяем, что исследуемая функция имеет в точке 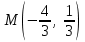 минимум. минимум. Найдем 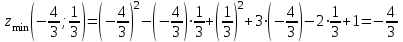 . .Нахождение наибольшего и наименьшего значения функции в замкнутой области Пусть требуется найти наибольшее и наименьшее значение функции  в некоторой замкнутой области D. Этих значений функция достигает либо во внутренних точках области, которые являются стационарными точками функции, либо на границах области. Значит, чтобы найти наибольшее и наименьшее значения функции в заданной замкнутой области, необходимо: в некоторой замкнутой области D. Этих значений функция достигает либо во внутренних точках области, которые являются стационарными точками функции, либо на границах области. Значит, чтобы найти наибольшее и наименьшее значения функции в заданной замкнутой области, необходимо:Найти стационарные точки, лежащие внутри области, и вычислить значения функции в этих точках; исследовать на экстремум эти точки нет необходимости; Найти наибольшее и наименьшее значение функции на границе области; если граница области состоит из нескольких участков, то исследование проводится для каждого участка в отдельности; Сравнить все полученные результаты, и выбрать среди них наибольшее и наименьшее значения. Пример. Найти наибольшее и наименьшее значение функции 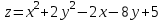 в замкнутом треугольнике, ограниченном осями координат и прямой в замкнутом треугольнике, ограниченном осями координат и прямой 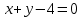 . .Решение. 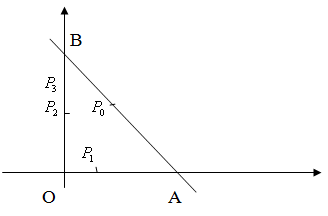 Находим стационарные точки: 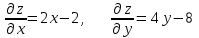 . .Из системы 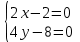 находим стационарную точку находим стационарную точку 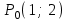 . Полученная точка лежит внутри заданной области. Вычислим значение функции в этой точке: . Полученная точка лежит внутри заданной области. Вычислим значение функции в этой точке: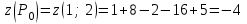 . .Найдем теперь наибольшее и наименьшее значения функции на границах области. Отрезок ОА задается уравнением 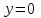 , а , а 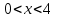 . При . При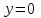 функция функция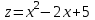 есть функция одной переменной х. Находим наибольшее и наименьшее значения этой функции на отрезке есть функция одной переменной х. Находим наибольшее и наименьшее значения этой функции на отрезке 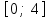 . .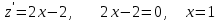 . .То есть  - стационарная точка, - стационарная точка, 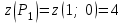 . .Вычислим значения функции на концах отрезка ОА:  Граница ОВ задается уравнением 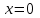 , а , а 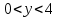 . При . При 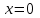 функция функция 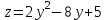 есть функция одной переменной у. Находим наибольшее и наименьшее значения этой функции на отрезке есть функция одной переменной у. Находим наибольшее и наименьшее значения этой функции на отрезке 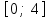 . .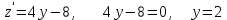 Значит 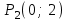 - стационарная точка, - стационарная точка, 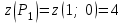 . .Значения функции на концах отрезка ОВ равны:  . .Отрезок АВ задается уравнением 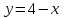 . Подставим это выражение в исходную функцию, получим функцию одной переменной: . Подставим это выражение в исходную функцию, получим функцию одной переменной: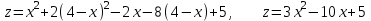 . .Найдем наибольшее и наименьшее значение этой функции на отрезке 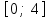 . .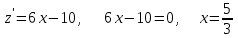 . .То есть 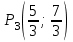 - стационарная точка, - стационарная точка,  . .Значения функции на концах отрезка АВ найдены ранее. Сравним полученные результаты и выберем среди них наибольшее и наименьшее значение функции в заданной замкнутой области. Итак, наибольшего значения функция достигает в точке 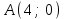 , а наименьшего - в точке , а наименьшего - в точке 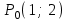 : : . .Вопросы для самоконтроля: 1.Что называется максимумом функции двух переменных? минимумом функции двух переменных? 2. Сформулируйте необходимое условие существования экстремума. 3. Сформулируйте достаточное условие существования экстремума. 4. Как находится наибольшее и наименьшее значение функции в заданной области? критерии оценки достижения обучающимися результатов обучения: Даны в силлабусе. рекомендуемая литература:Дана в силлабусе. |
