Лабораторная работа 1. Лекция Понятие модели и моделирования. Классификация моделей. Компьютерное математическое моделирование

• Название: Лекция Понятие модели и моделирования. Классификация моделей. Компьютерное математическое моделирование
• Дата: 14.11.2022
• Размер: 0.53 Mb.
• Имя файла: Лабораторная работа 1.docx
• Тип: Лекция; #786936

Лабораторная работа 1

Тема 3. Модели решения функциональных и вычислительных задач

Лекция 3.1. Понятие модели и моделирования. Классификация моделей. Компьютерное математическое моделирование

Задание

Для некоторой математической модели задана таблица значений (x_i,y_i)функции y₌ f(x). Требуется определить аппроксимирующую функцию (x), которую можно применить для вычисления приближенных значений функции f(x). Используя функцию (x), найти приближенное значение y для заданного значения х.

Данные для расчетов выбираются в соответствии с номером варианта из табл. 2.

Вариант выполнения задания выбирается студентом из табл. 1.

Выполненное задание сохраняется в файле Лаб_работа_1_Фамилия.xlsx или Лаб_работа_1_Фамилия.xls.

Таблица 1

Таблица выбора вариантов

Первая буква фамилии студента	А Л H	Б О Ч	В П Ю	Г М Р	Д С Ш	Е Ё Т	Ж У Щ	З Я Ф	И Х Э	К Ц Ы
Номер варианта	1	2	3	4	5	6	7	8	9	10

Таблица 2

Варианты

Номер варианта	xi	2	4	5	6	8	9	11	12	13	15	16	18	Значение xдля расчета y
1	yi	3	6	6	6	10	9	12	14	15	16	17	19	20
2	yi	5	9	10	13	17	19	23	26	28	28	29	30	21
3	yi	7	13	16	19	25	28	34	38	41	45	47	50	20
4	yi	9	15	20	22	33	37	45	50	54	56	60	63	21
5	yi	11	18	20	31	40	44	56	62	67	70	76	78	20
6	yi	11	26	31	40	49	58	68	74	80	85	89	93	21
7	yi	15	29	36	43	57	64	78	86	92	98	103	106	20
8	yi	17	33	40	48	65	73	88	104	106	114	116	122	21
9	yi	6	10	12	17	18	20	22	28	29	30	33	35	20
10	yi	8	14	17	20	26	29	36	39	42	46	49	55	21

Рекомендации по выполнению работы

Для решения задачи можно использовать инструмент построения линий тренда в Microsoft Excel, выполнив следующие шаги:

• 
  построить точечную диаграмму по заданной таблице значений (x_i,y_i);
  
• 
  построить линии тренда, используя аппроксимацию табличных значений функции y разными методами: линейной аппроксимацией, аппроксимацией с помощью полинома второго порядка, аппроксимацией степенной функцией и другое;
  
• 
  оценить близость полученных функций табличным данным посредством сравнения значений коэффициента достоверности R^2 для разных видов аппроксимации;
  
• 
  выполнить расчет приближенного значения y для заданного значения x, используя способ аппроксимации, отвечающий наибольшему значению R^2.
  

Образец выполнения лабораторной работы

Выполним задание для данных, представленных в следующей таблице:

xi	1	3	4	5	6	8	10	11	12	13	14	16
yi	11	21	27	45	55	68	78	83	83	89	92	93

Для нахождения значения y будем использовать x= 18.

Оформим таблицу с данными на рабочем листе электронной таблицы так, как показано на рис. 1. Построим по данным таблицы диаграмму точечного типа. Для этого выделим данные и выполним команды «Вставка – Диаграммы – Точечная».

Наведем курсор мыши на любую точку построенного графика и нажмем правую кнопку. В появившемся контекстном меню следует выбрать команду «Добавить линию тренда…». Откроется диалоговое окно «Формат линии тренда» (рис. 2), в котором выберем тип линии тренда «Линейная» и установим флажки «Показывать уравнение на диаграмме» и «Поместить на диаграмму величину достоверности аппроксимации (R^2)».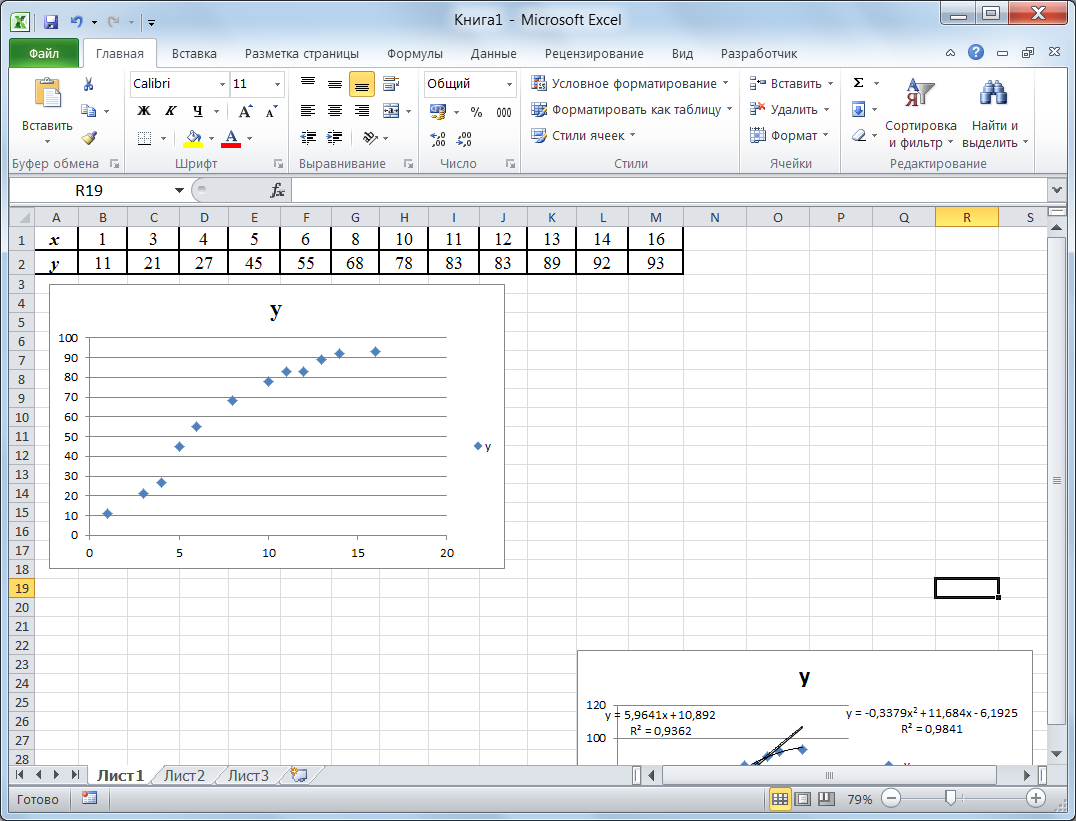



Рис. 1. Точечная диаграмма, соответствующая таблице значений функции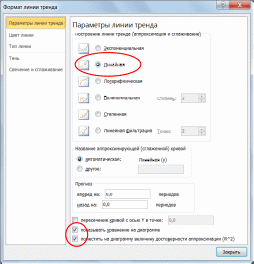



Рис. 2. Выбор типа линии тренда

К диаграмме будет добавлена линия тренда, построенная по методу наименьших квадратов для случая линейной аппроксимации. Кроме того, будет выведен вид линейной аппроксимирующей функции y = 5,9641x + 10,892и коэффициент достоверности аппроксимации R^2 = 0,9362 (см. рис. 3).

Аналогично построим линии тренда с использованием полинома второго порядка и степенной функции.

Величина достоверности аппроксимации характеризует степень близости аппроксимирующей функции к данным таблицы, по которой было выполнена аппроксимация. Чем ближе R^2 к 1, тем более достоверной является аппроксимация.

Сравнение значений величин достоверности аппроксимации для разных аппроксимирующих функций в нашем случае показывает, что наибольшее значение R^2 = 0,9841 соответствует аппроксимации с помощью полинома второго порядка.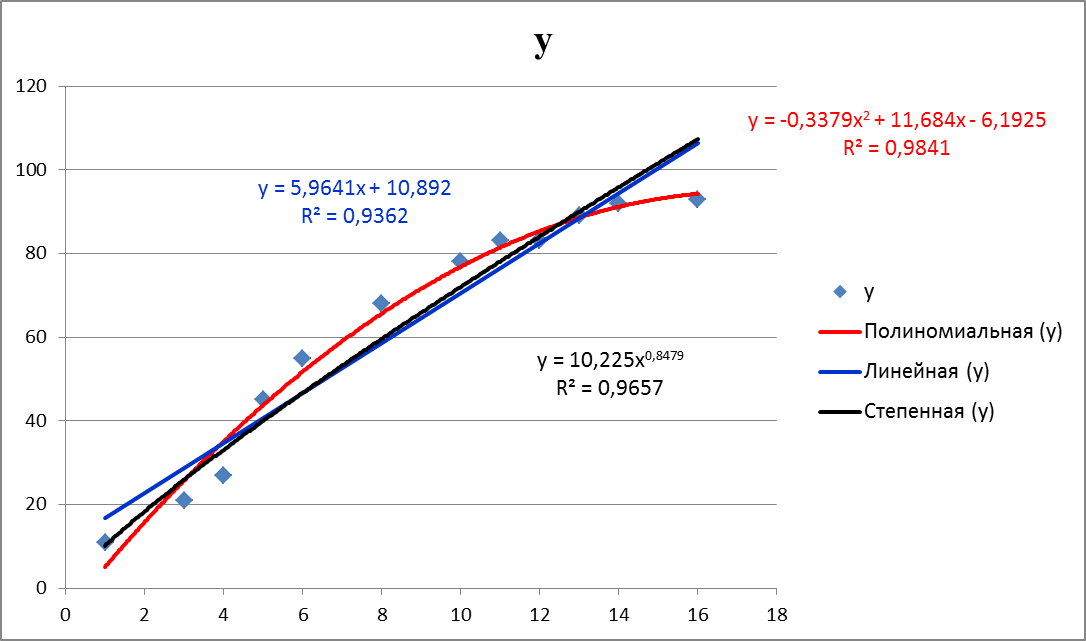



Рис. 3. Линии тренда на диаграмме

Используем полученную полиномиальную функцию для вычисления значения y для x= 18. Для этого в ячейку N2 введем значение 18, а в ячейку O2 – формулу для расчета y: = – 0,3379 · N2^2 + 11,684 · N2 – 6,1925.

Расчет показывает, что для x= 18 приближенное значение y, полученное с помощью аппроксимирующей функции, равно 94,64 (рис. 4).


Рис. 4. Результат выполнения задания