реферат_1. Линейные и нелинейные структуры данных
 Скачать 319.54 Kb. Скачать 319.54 Kb.
|

Кафедра экономики природообустройства Реферат по дисциплине «Менеджмент» на тему: «Линейные и нелинейные структуры данных»
Москва, 2021 г. СодержаниеВведение 3 1. Классификация типов и структур данных 4 2. Линейные и нелинейные структуры данных 9 2.1 Стеки, очереди, деки и списки 9 2.2 Деревья, графы 15 Заключение 19 Список используемых источников 22 ВведениеАктуальность выбранной темы исследования заключается в том, что типы и структуры данных составляют фундамент, на основе которого строится вся современная технология программирования. Понятие структуры данных можно определить следующим образом - это некоторая программная единица, дающая возможность хранить и обрабатывать множество однотипных и/или логически связанных данных. При этом реализуется возможность добавления, поиска, изменения и удаления данных в множестве посредством набора функций. Структуры данных формируются с помощью типов данных, ссылок и операций над ними в конкретном языке программирования. Различные виды структур данных подходят для различных приложений, при этом часть из них имеют узкую специализацию для определённых задач. Фундаментальными блоками для большей части структур данных являются массивы, записи, размеченные объединения и указатели. Объектом исследования являются структуры данных. Предметом исследования являются линейные и нелинейные структуры данных. Цель работы – выявить особенности линейных и нелинейных структур данных. Для достижения поставленной цели в работе были сформулированы следующие задачи: - рассмотреть классификацию типов и структур данных; - проанализировать особенности построения стеков, очередей, деков и список данных; - выявить особенности построения деревьев и графов. Вопросы исследования линейных и нелинейных структур данных постоянно обсуждаются отечественными и зарубежными специалистами, среди которых следует отметить работы 1. Классификация типов и структур данныхВ настоящее время выделяют различные классификации типов и структур данных. Можно выделить следующие категории типов данных [2, стр. 88]: Встроенные типы данных, т.е. типы, предопределенные в языке программирования или языке базы данных. Как правило, в языке фиксируется внешнее представление значений этих типов (вид литеральных констант, например, «integer», «char», «boolean» и др.) и набор операций с описанием их семантики. Уточняемый тип данных - в данном случае понимается возможность определения типа на основе встроенного типа данных, значения которого упорядочены. Суть состоит в том, что для любого значения любого встроенного типа существует его внешнее литеральное представление, а по литеральному представлению константы можно однозначно определить тип, к которому она относится. Если к тому же на множестве значений типа задано отношение порядка (определены операции сравнения), то иногда в приложении возникает потребность использовать подмножество значений такого типа, ограниченное некоторым однозначно определенным диапазоном. Наличие упорядоченности значений дает возможность задать такой диапазон парой литеральных констант базового типа c1 и c2, удовлетворяющих условию c1 <= c2. Таким образом, определение нового уточненного типа может иметь вид (пример из языка Модула-2): TYPE T = [c1..c2]. Перечисляемые типы данных представляют собой множества, состоящие из конечного числа упорядоченных именованных значений. В классическом варианте определение типа состоит из перечисления имен значений, эти имена в дальнейшем играют роль имен литеральных констант этого типа и должны отличаться от литерального изображения констант любого другого типа. Поскольку значения типа задаются путем перечисления, каждому значению можно однозначно сопоставить натуральное число от 1 до n, где n - число значений перечисляемого типа. Как правило, для любого перечисляемого типа предопределяются операции получения значения по его номеру и получения номера по значению. Кроме того, для перечисляемого типа предопределяются операции сравнения и получения следующего и предыдущего значения. Конструируемые или составные типы обладают той особенностью, что в языке предопределены средства спецификации таких типов и некоторый набор операций, дающих возможность доступа к компонентам составных значений. К данной категории можно отнести типы массивов, записей и множеств. Указательные типы предоставляют возможность работы с типизированными множествами абстрактных адресов переменных, содержащих значения некоторого типа. Понятие указателя в языках программирования представляет собой абстракцию понятия машинного адреса, а именно: при наличии машинного адреса есть возможность обратиться к нужному элементу памяти, аналогично, имея значение указателя, можно обратиться к соответствующей переменной. Определяемый пользователем, или абстрактный, тип данных. Здесь понимается возможность полного определения нового типа, включая явную или неявную спецификацию множества значений, спецификацию внутреннего представления значений типа и спецификацию набора операций над значениями определяемого типа. В отношении классификации структур данных, то в общем случае различают простые и интегрированные структуры данных. Простыми называются такие структуры данных, которые не могут быть разбиты на составные части размером больше бита [4, cтр.75]. С точки зрения физической структуры важным является то обстоятельство, что в каждой конкретной машинной архитектуре и конкретной среде программирования всегда можно заранее сказать, каким будет размер данного простого типа, и какой будет структура его размещения в памяти. С логической точки зрения простые данные являются неделимыми единицами. Интегрированными называются такие структуры данных, составными частями которых являются другие структуры данных - простые или в свою очередь интегрированные. Интегрированные структуры данных конструируются программистом с использованием средств интеграции данных, предоставляемых языками программирования. В зависимости от отсутствия или наличия явно заданных связей между элементами данных можно классифицировать несвязные структуры (векторы, массивы, строки, стеки, очереди) и связные структуры (связные списки) [6, cтр.45]. По признаку изменчивости различают структуры статические, полустатические и динамические. Классификация структур данных по признаку изменчивости приведена на рисунке 1.  Рисунок 1 Классификация структур данных Здесь необходимо отметить, что базовые, статические, полустатические и динамические структуры данных характерны для оперативной памяти и часто также называются оперативными структурами. Файловые структуры соответствуют структурам данных для внешней памяти. Также выделяют классификацию линейных и нелинейных структур данных. К линейным структурам данных относятся статические структуры данных, которые позволяют зафиксировать диапазон значений, присваиваемых этим переменным. Виды линейных структур данных приведены в таблице 1. Таблица 1 – Виды линейных структур данных
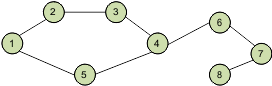
Необходимо отметить, что дек является более универсальной структурой данных по сравнению с другими описанными в таблице 1, поскольку позволяет накладывать дополнительные ограничения на операции, а также с ним можно выполнять моделирование стека и очереди [8, cтр.106]. Дек можно реализовать как статическую структуру данных в виде одномерного массива и как динамическую структуру в виде линейного списка, поскольку в деке осуществляется с концами структуры. К нелинейным структурам данных относятся виды, приведенные на рисунке 2.  Рисунок 2 – Виды нелинейных структур данных В элементах мультисписка важно различать поля указателей для разных списков, чтобы можно было проследить элементы одного списка, не вступая в противоречие с указателями другого списка, а отличием разделенных список является то, что они имеют дополнительный указатель. Элементы разделенного (слоеного) списка группируются по определенному признаку, первый элемент каждой группы содержит указатель на первый элемент следующей группы и если следующая группа отсутствует или элемент не является первым в группе, то этот дополнительный указатель принимает значение nil. 2. Линейные и нелинейные структуры данных2.1 Стеки, очереди, деки и спискиСтек, дек и очередь представляют собой частные случаи односвязных списков, для которых определен только операции добавления/удаления элементов только из начала или конца списка. Стек – это упорядоченный набор элементов, в котором добавление новых и удаление существующих элементов разрешено только с одного конца, который называется вершиной стека [1, cтр.180]. Стек называют структурой типа LIFO (Last In - First Out) последним пришел - первым ушел. Стек похож на стопку с подносами, уложенными один на другой – чтобы достать какой-то поднос необходимо снять все подносы, которые лежат на нем, а положить новый поднос можно только сверху всей стопки. На рисунке 3 изображен стек из 6 элементов. 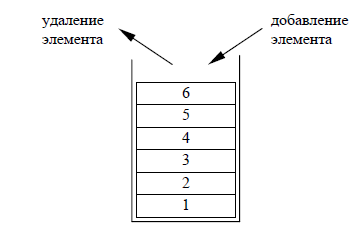 Рисунок 3 Схематическое представление стека В современных компьютерах стек используется: для размещения локальных переменных, параметров процедуры или функции или для сохранения адреса возврата (по какому адресу необходимо вернуться из процедуры), временного хранения данных. Для стека выделяется ограниченная область памяти. При каждом вызове процедуры в стек добавляются новые элементы, поэтому если вложенных вызовов будет много, стек переполнится. Очень опасной в отношении переполнения стека является ошибочная реализация рекурсии, поскольку она как раз и предполагает бесконечные вложенные вызовы одной и той же процедуры или функции. Очередь - это упорядоченный набор элементов, в котором добавление новых элементов допустимо с конца очереди, а удаление существующих элементов – только с начала очереди [3, cтр.96]. Очередь называют структурой типа FIFO (First In - First Out) - первым пришел, первым ушел. Очередь проще всего представить себе в виде очереди в магазине. Как и стек, очередь можно реализовать с помощью массива или двусвязного списка. В отличие от стека у очереди «подвижны» оба конца. Поэтому чтобы не сдвигать все элементы в массиве при удалении или добавлении элемента, обычно использую две переменные Start и Finish – первая из них обозначает номер первого элемента в очереди, а вторая – номер последнего. Если они равны, то в очереди всего один элемент. Массив замыкается в кольцо – если массив закончился, но в начале массива есть свободные места, то новый элемент добавляется в начало массива, как показано на рисунке 4.  Рисунок 4 Очередь Для работы с очередью необходимо определить, как выполняются две операции – добавление элемента в конец очереди (Push Finish) и удаление элемента с начала очереди (Pop). Данные операции приведены в приложении 1. Дек - это упорядоченный набор элементов, в котором добавление новых и удаление существующих элементов допустимо с любого конца. Дек также может быть реализован на основе массива или двусвязного списка. Так как для дека разрешены операции добавления/удаления элемента в начало/конец, то их можно реализовать, используя приведенные выше процедуры для стека и очереди. В списке каждый элемент связан со следующим и, возможно, с предыдущим. В первом случае список называется односвязным, во втором - двусвязным. Также применяются термины однонаправленный и двунаправленный. Если последний элемент связать указателем с первым, получается циклический список. Количество элементов в списке может изменяться в процессе работы программы. Каждый элемент списка содержит ключ, идентифицирующий этот элемент. Ключ обычно бывает либо целым числом, либо строкой и является частью данных, хранящихся в каждом элементе списка. В качестве ключа в процессе работы со списком могут выступать разные части данных. Например, если создается список из записей, содержащих фамилию, год рождения, стаж работы и пол, любая часть записи может выступать в качестве ключа: при упорядочивании списка по алфавиту ключом будет фамилия, а при поиске, например, ветеранов труда ключом можно сделать стаж. Ключи разных элементов списка могут совпадать. Над списками можно выполнять следующие операции [7, cтр.180]: - добавление элемента в конец списка; - чтение элемента с заданным ключом; - вставка элемента в заданное место списка; - удаление элемента с заданным ключом; - упорядочивание списка по ключу. Список не обеспечивает произвольный доступ к элементу, поэтому при выполнении операций чтения, вставки и удаления выполняется последовательный перебор элементов, пока не будет найден элемент с заданным ключом. Для списков большого объема перебор элементов может занимать значительное время, поскольку среднее время поиска элемента пропорционально количеству элементов в списке. Односвязный список – это простейший случай, когда каждый узел содержит всего одну ссылку на следующий элемент. У последнего в списке элемента поле ссылки содержится NULL. Чтобы не потерять список, нужно где-то хранить адрес его первого узла – он называется «головой» списка. Односвязный список в программе объявляется следующим образом: необходимо объявить два новых типа данных – узел списка и указатель на него. Узел представляет собой структуру, которая содержит три поля – значение элемента, целое число и указатель на такой же узел. Следует обратить внимание, что при записи данных в узел используется обращение к полям структуры через операцию «». После создания новый узел необходимо поместить в начало, в конец или в середину списка. При добавлении нового узла New Unit в начало списка необходимо выполнить действия, приведенные на рисунке 5. 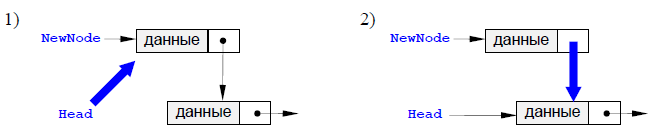 Рисунок 5 Добавление узла в начало списка Как видно из рисунка 5, в данном случае необходимо установить ссылку узла New Unit на голову существующего списка, а также создать голову списка на новый узел. Пример добавления узла после заданного значения приведен на рисунке 6.  Рисунок 6 Добавление узла после заданного Как видно из рисунка 6, данная операция выполняется посредством установки ссылку нового узла на узел, следующий за данным узлом, а затем установки данного узла p на New Unit. Последовательность операций менять нельзя, потому что если сначала поменять ссылку у узла p, будет потерян адрес следующего узла. Добавление узла перед заданным значением является самой сложной схемой добавления. Проблема заключается в том, что в простейшем односвязном списке для того, чтобы получить адрес предыдущего узла, нужно пройти весь список сначала. Удаление узла также связано с поиском заданного узла по всему списку, так как нужно поменять ссылку у предыдущего узла, а перейти к нему непосредственно невозможно. Если найден узел, за которым идет удаляемый узел, необходимо просто переставить ссылку (рисунок 7).  Рисунок 7 Удаление узла Есть и другой способ упростить работу с односвязным списком - хранить в памяти указатель не только на следующий, но и на предыдущий элемент списка. В этом случае для доступа к списку используется не одна переменная-указатель, а две – ссылка на «голову» списка (Start) и на «хвост» - последний элемент (Finish) (рисунок 8).  Рисунок 8 Структура двусвязного списка Помимо значимых данных каждый узел списка содержит также ссылку на следующий за ним узел (поле next) и предыдущий (поле prev). Поле next у последнего элемента и поле prev у первого содержат NULL. При добавлении нового узла New Unit в начало списка необходимо использовать последовательность, приведенную на рисунке 9.  Рисунок 9 Добавление элемента двусвязного списка Рисунок 9 Добавление элемента двусвязного спискаКак видно из рисунка 9 в данном случае вначале необходимо установить указатель next узла New Unit на голову существующего списка и его указатель prev в NULL. Далее нужно установить указатель prev бывшего первого узла (если он существовал) на New Unit. После этого установить голову списка на новый узел. Если в списке не было ни одного элемента, хвост списка также устанавливается на новый узел. Благодаря симметрии добавление нового узла New Unit в конец списка проходит совершенно аналогично, достаточно в указанной выше процедуре необходимо везде поменять местами Start на Finish, а также поменять prev и next. Добавление элемента двусвязного списка после заданного приведено на рисунке 10.  Рисунок 10 Добавление элемента двусвязного списка после заданного Как видно из рисунка 10 в данном случае необходимо установить ссылки нового узла на следующий за данным (next) и предшествующий ему (prev), а также установить ссылки соседних узлов так, чтобы включить New Unit в список. Для удаления узла также требуются указатели на голову и хвост списка, поскольку они могут измениться при удалении крайнего элемента списка. На первом этапе устанавливаются ссылки соседних узлов (если они есть) так, как если бы удаляемого узла не было бы. Затем узел удаляется и память, которую он занимает, освобождается. Эти этапы показаны на рисунке 11.  Рисунок 11 Удаление элемента двусвязного списка Иногда список (односвязный или двусвязный) замыкают в кольцо, то есть указатель next последнего элемента указывает на первый элемент, и (для двусвязных списков) указатель prev первого элемента указывает на последний. 2.2 Деревья, графы Дерево – это совокупность узлов (вершин) и соединяющих их направленных ребер (дуг), причем в каждый узел, за исключением корня, ведет ровно одна дуга. Корень – это начальный узел дерева, в который не ведет ни одной дуги. Например, генеалогическое дерево - в корне дерева находится человек, от него идет две дуги к его родителям, от каждого из родителей - две дуги к их родителям [5, cтр.48]. На рисунке 12 приведены структуры, из которых а) и б) являются деревьями, а в) и г) - нет.  Рисунок 12 Пример дерева и не дерева Предком для узла x называется узел дерева, из которого существует путь в узел x. Потомком узла x называется узел дерева, в который существует путь (по стрелкам) из узла x. Родителем для узла x называется узел дерева, из которого существует непосредственная дуга в узел x. Сыном узла x называется узел дерева, в который существует непосредственная дуга из узла x. Уровнем узла x называется длина пути (количество дуг) от корня к данному узлу. Считается, что корень находится на уровне 0. Листом дерева называется узел, не имеющий потомков. Внутренней вершиной называется узел, имеющий потомков. Высотой дерева называется максимальный уровень листа дерева. Упорядоченным деревом называется дерево, все вершины которого упорядочены (то есть имеет значение последовательность перечисления потомков каждого узла). Дерево представляет собой типичную рекурсивную структуру, которая определяет саму себя. Как и любое рекурсивное определение, определение дерева состоит из двух частей – первая определяет условие окончания рекурсии, а второе – механизм ее использования [1, cтр.46]. На практике главным образом применяются деревья особого вида, называемые двоичными или бинарными. Двоичным деревом называется дерево, каждый узел которого имеет не более двух сыновей. Двоичные деревья упорядочены, то есть различают левое и правое поддеревья. Строго двоичным деревом называется дерево, у которого каждая внутренняя вершина имеет непустые левое, правое поддеревья. Это означает, что в строго двоичном дереве нет вершин, у которых есть только одно поддерево. На рисунке 13 даны деревья, а) и б) являются строго двоичными, а в) и г) – нет.  Рисунок 13 Двоичные деревья Полным двоичным деревом называется дерево, у которого все листья находятся на одном уровне и каждая внутренняя вершина имеет непустые левое и правое поддеревья. На рисунке выше только дерево а) является полным двоичным деревом. Вершина дерева, как и узел любой динамической структуры, имеет две группы данных: полезную информацию и ссылки на узлы, связанные с ним. Для двоичного дерева таких ссылок должно быть две – ссылка на левого сына и ссылка на правого сына. Граф – совокупность точек, соединенных линиями. Точки называются вершинами, или узлами, а линии – ребрами, или дугами. Степень входа вершины – количество входящих в нее ребер, степень выхода – количество исходящих ребер [5, cтр.67]. Граф, содержащий ребра между всеми парами вершин, является полным. Пример построения графа приведен на рисунке 14.  Рисунок 14 – Пример построения графа Встречаются такие графы, ребрам которых поставлено в соответствие конкретное числовое значение, они называются взвешенными графами, а это значение – весом ребра. Когда у ребра оба конца совпадают, т.е. оно выходит из вершины и входит в нее, то такое ребро называется петлей. Графы бывают связанными и не связанными. Примеры построения связанных и не связанных графов приведены на рисунке 15.
Рисунок 15 – Примеры построения связанных и не связанных графов В связном графе между любой парой вершин существует как минимум один путь. В несвязном графе существует хотя бы одна вершина, не связанная с другими. Графы также бывают ориентированными, неориентированными и смешанными. Пример построения ориентированных и неориентированных графов приведен на рисунке 16.
Рисунок 16 – Примеры построения ориентированных и неориентированных графов В ориентированном графе ребра являются направленными, т.е. существует только одно доступное направление между двумя связными вершинами. В неориентированном графе по каждому из ребер можно осуществлять переход в обоих направлениях. Частный случай двух этих видов – смешанный граф. Он характерен наличием как ориентированных, так и неориентированных ребер. ЗаключениеВ процессе написания работы были выявлены особенности линейных и нелинейных структур данных. На первоначальном этапе была рассмотрена классификация типов и структур данных и установлено, что по категориям типов данных выделяют встроенные, перечисляемые, конструируемые, указательные типы данных и типы данных определяемые пользователем. В структуре данных выделяют простые базовые, статистические, полустатистические, динамические и файловые структуры данных. Также существует классификация с выделением линейных и нелинейных структур данных. К линейным структурам данных относятся массив, строка, запись, множество, таблица, список, стек, разреженные матрицы, очередь и дек. К нелинейным структурам данных относятся мультисписок, разделенные списки, граф и дерево. В работе более детально были рассмотрены стеки, очереди, деки и списки. Было установлено, что стек, дек и очередь представляют собой частные случаи односвязных списков, для которых определен только операции добавления/удаления элементов только из начала или конца списка. Стек выступает упорядоченным набором элементов, в котором добавление новых и удаление существующих элементов разрешено только с одного конца, который называется вершиной стека. Очередь выступает упорядоченным набором элементов, в котором добавление новых элементов допустимо с конца очереди, а удаление существующих элементов – только с начала очереди. В свою очередь дек выступает упорядоченным набором элементов, в котором добавление новых и удаление существующих элементов допустимо с любого конца. Было установлено, что в списке каждый элемент связан со следующим и, возможно, с предыдущим. В первом случае список называется односвязным, во втором - двусвязным. Также применяются термины однонаправленный и двунаправленный. Если последний элемент связать указателем с первым, получается циклический список. Количество элементов в списке может изменяться в процессе работы программы. Дерево является совокупностью узлов (вершин) и соединяющих их направленных ребер (дуг), причем в каждый узел, за исключением корня, ведет ровно одна дуга. Корень – это начальный узел дерева, в который не ведет ни одной дуги. Дерево представляет собой типичную рекурсивную структуру, которая определяет саму себя. Как и любое рекурсивное определение, определение дерева состоит из двух частей – первая определяет условие окончания рекурсии, а второе – механизм ее использования. Анализ показал, что на практике главным образом применяются деревья особого вида, называемые двоичными или бинарными. Двоичным деревом называется дерево, каждый узел которого имеет не более двух сыновей. Граф – совокупность точек, соединенных линиями. Точки называются вершинами, или узлами, а линии – ребрами, или дугами. Степень входа вершины – количество входящих в нее ребер, степень выхода – количество исходящих ребер. В ориентированном графе ребра являются направленными, т.е. существует только одно доступное направление между двумя связными вершинами. В неориентированном графе по каждому из ребер можно осуществлять переход в обоих направлениях. Частный случай двух этих видов – смешанный граф. Он характерен наличием как ориентированных, так и неориентированных ребер. Список используемых источниковАлексеев В.Е. Структуры данных и модели вычислений: учеб. пособие/ В.Е. Алексеев, В.А. Таланов. – Москва: Интернет-Университет Информационных Технологий (ИНТУИТ), Ай Пи Ар Медиа, 2021. – 247 c. Волков М.М. Структуры и алгоритмы обработки данных: учеб. пособие / М. М. Волков. – Москва: Московский технический университет связи и информатики, 2016. – 16 c. Костюкова Н.И. Комбинаторные алгоритмы для программистов: учеб. пособие/ Н.И. Костюкова. – Москва, Саратов: Интернет-Университет Информационных Технологий (ИНТУИТ), Ай Пи Ар Медиа, 2020. – 216 c. Курапова Е.В. Структуры и алгоритмы обработки данных: практикум/ Е.В. Курапова, Е.П. Мачикина. – Новосибирск: Сибирский государственный университет телекоммуникаций и информатики, 2015. – 23 c. Ландовский В.В. Алгоритмы обработки данных: учеб. пособие/ В.В. Ландовский. – Новосибирск: Новосибирский государственный технический университет, 2018. – 67 c. Медведев Д.М. Структуры и алгоритмы обработки данных в системах автоматизации и управления: учеб. пособие/ Д.М. Медведев. – Саратов: Медиа, 2018. – 100 c. Мейер Б. Инструменты, алгоритмы и структуры данных: учеб. пособие/ Б. Мейер. – Москва: Интернет-Университет Информационных Технологий (ИНТУИТ), Ай Пи Ар Медиа, 2021. – 540 c. Окулов С.М. Абстрактные типы данных: учеб. пособие / С.М. Окулов. – Москва: Лаборатория знаний, 2020. – 251 c. |