Контрольная работа по математике. Математическое ожидание находим по формуле m x
 Скачать 16.18 Kb. Скачать 16.18 Kb.
|
Математическое ожидание находим по формуле m = ∑xipi. Математическое ожидание M[X]. M[x] = (-6)*0.1 + (-2)*0.3 + 1*0.4 + 4*0.2 = 0 Дисперсию находим по формуле d = ∑x2ipi - M[x]2. Дисперсия D[X]. D[X] = 62*0.1 + 22*0.3 + 12*0.4 + 42*0.2 - 02 = 8.4 Среднее квадратическое отклонение σ(x). Функция распределения F(X). F(x≤-6) = 0 F(-6< x ≤-2) = 0.1 F(-2< x ≤1) = 0.3 + 0.1 = 0.4 F(1< x ≤4) = 0.4 + 0.4 = 0.8 F(x>4) = 1 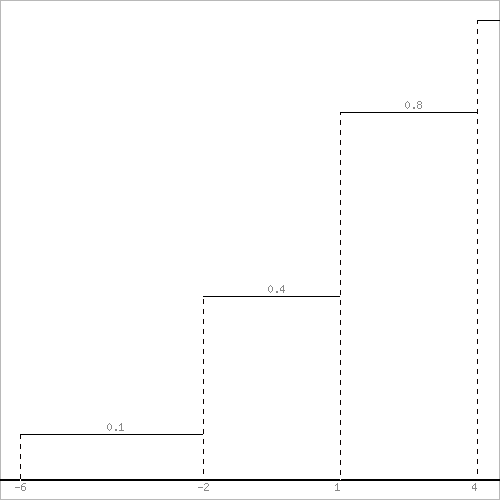 Коэффициент вариации - мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс. Поскольку v ≤ 30%, то совокупность однородна, а вариация слабая. Наиболее точным и распространенным показателем асимметрии является моментный коэффициент асимметрии. As = M3/σ3 где M3 - центральный момент третьего порядка.
As = -10.8/24.346 = -0.44 Отрицательный знак свидетельствует о наличии левосторонней асимметрии Для симметричных распределений рассчитывается показатель эксцесса (островершинности). Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения. Чаще всего эксцесс оценивается с помощью показателя: где M4 - центральный момент четвертого порядка. Решение было получено и оформлено с помощью сервиса: Математическое ожидание дискретной случайной величины С этой задачей также решают: Система случайных величин Уравнение парной линейной регрессии Проверка гипотезы о виде распределения Теория вероятностей онлайн Доверительный интервал |
