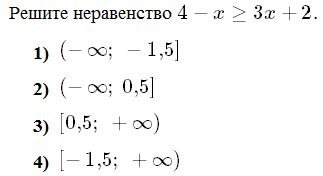варианты гвэ. Материалы для подготовки к государственному выпускному экзамену по математике для обучающихся по образовательным программам
 Скачать 1.93 Mb. Скачать 1.93 Mb.
|
|
МАТЕМАТИКА ГВЭ Тренировочные материалы для подготовки к государственному выпускному экзамену по МАТЕМАТИКЕ для обучающихся по образовательным программам ОСНОВНОГО общего образования ПОЯСНИТЕЛЬНАЯ ЗАПИСКА В сборнике представлены тренировочные материалы для подготовки к ГВЭ по математике в письменной форме. Задания подобраны таким образом, чтобы охватить все основные разделы школьного курса математики основной школы. Задания с выбором подразумевают выбор верного ответа из четырёх вариантов. Задания с кратким ответом подразумевают только числовой ответ в виде целого числа или конечной десятичной дроби. Частный случай задания с кратким ответом – задание с множественным выбором, где требуется указать одно или несколько верных утверждений из предложенного перечня. Ответом в данном случае являются номера верных вариантов ответа, записанных в любом порядке без пробелов и других вспомогательных символов. Например, если верные варианты имеют номера 1) и 3), то ответ может быть записан в виде 13 или 31. Другой частный случай – задание на установление соответствия в модуле «Алгебра». Ответ представляет собой упорядоченную последовательность цифр, каждая из которых записывается в соответствующую ячейку таблицы. Каждая задача с кратким ответом снабжена полем «Ответ». Задания с развёрнутым ответом подразумевают полное обоснованное решение и запись ответа в произвольной форме. При выполнении заданий с развёрнутым ответом следует уделять внимание полноте и грамотности математической записи. При этом можно пользоваться без ссылок и обоснований всеми фактами, утверждениями, теоремами курса математики основной и полной средней школы (содержащихся в учебниках и учебных пособиях, допущенных или рекомендованных Министерством образования и науки РФ). Задания с развёрнутым ответом имеют повышенный уровень сложности. Задания выбраны из открытых банков математических заданий для проведения итоговой аттестации и могут быть включены в экзаменационные материалы ГВЭ-9. Инструкция по выполнению работы Экзаменационная работа состоит из 12 заданий, из которых10 заданий базового уровня сложности с кратким ответом и 2 задания повышенного уровня сложности с развёрнутым ответом. Ответы к заданиям 1–10 записываются в виде целого числа или конечной десятичной дроби. В случае записи неверного ответа зачеркните его и запишите рядом новый. Каждое верно выполненное задание оценивается 1 баллом. При выполнении заданий 11 и 12 требуется записать полное решение и ответ. Критерии оценивания заданий 11 и 12 Количество баллов, выставляемых за выполнение заданий 11 и 12,зависит от полноты решения и правильности ответа. Общие требования к выполнению заданий с развёрнутым ответом: решение должно быть математически грамотным, полным, в частности всевозможные случаи должны быть рассмотрены. Методы решения, формы его записи и формы записи ответа могут быть разными. За решение, в котором обоснованно получен правильный ответ, выставляется максимальное количество баллов. Правильный ответ при отсутствии текста решения оценивается в 0 баллов. Эксперты проверяют только математическое содержание представленного решения, а особенности записи не учитывают. В критериях оценивания конкретных заданий содержатся общие требования к выставлению баллов. При выполнении задания можно использовать без доказательства и ссылок любые математические факты, содержащиеся в учебниках и учебных пособиях, входящих в Федеральный перечень учебников. При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы. Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать Максимальный первичный балл за выполнение всей работы – 14. Задание с развернутым ответом оценивается двумя экспертами. Существенным считается расхождение в 2 и более балла оценки за выполнение задания с развернутым ответом. Если расхождение баллов, выставленных двумя экспертами за выполнение одного из заданий 11 или 12, составляет 2 балла, то третий эксперт проверяет только ответы на те задания, которые вызвали столь существенное расхождение. Если имеется расхождение баллов, выставленных двумя экспертами за выполнение заданий 11 и 12, в сумме 2 или более баллов, то третий эксперт проверяет ответы на оба эти задания. Продолжительность выполнения экзаменационной работы участниками ОГЭ с ОВЗ, детьми-инвалидами и инвалидами по математике составляет 5 часов 25 минут. Учащимся разрешается использовать справочные материалы, содержащие основные формулы курса математики, выдаваемые вместе с работой (входят в состав контрольных измерительных материалов). Разрешается использовать линейку. Калькуляторы на экзамене не используются. Рекомендуется следующая шкала перевода суммы первичных баллов в пятибалльную систему оценивания:
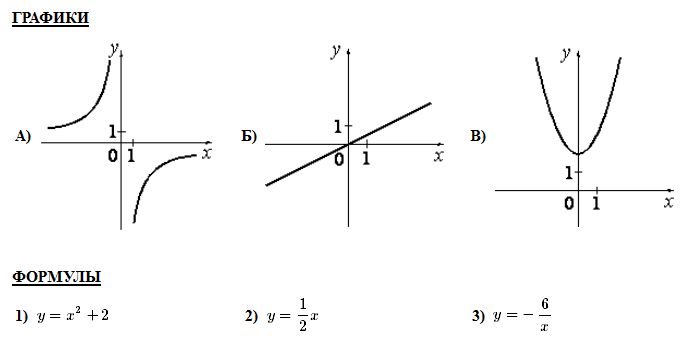
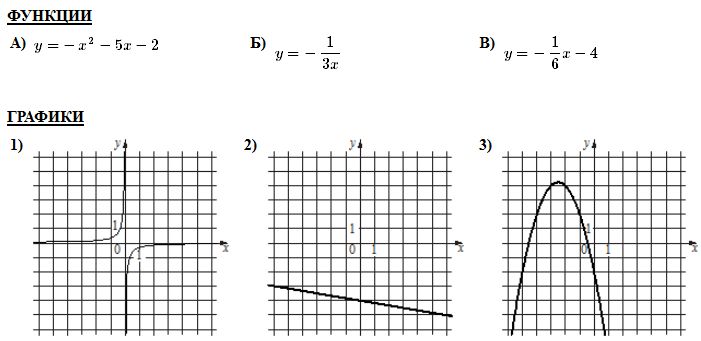
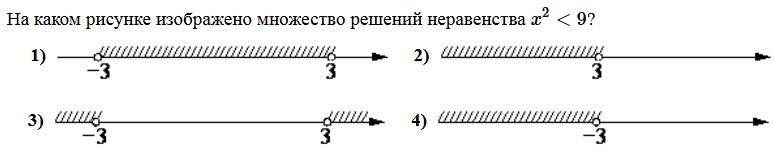
  Вариант1 Часть 1. 1. Найдите значение выражения 2. Найдите корень уравнения 9х + 1 = 10х - 1. 3. Найдите значение выражения 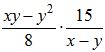 при х = -1, у = 8. при х = -1, у = 8.4. Установите соответствие между функциями и их графиками. А) y = -2x + 4 Б) y = 2x - 4 В) y = 2x +4 Запишите в ответ выбранные цифры в порядке соответствия АБВ. 1) 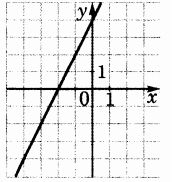 2) 2) 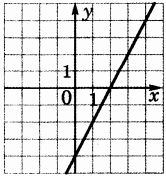 3) 3) 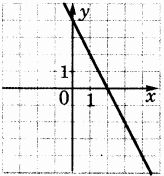 5. Укажите решение неравенства 6. Найдите площадь ромба, если его диагонали равны 34 и 4. 7. В треугольнике АВС известно, что АС = 16, ВС = 12, угол С равен 900. Найдите радиус описанной около этого треугольника окружности. 8. Какие из следующих утверждений верны? 1) сумма углов прямоугольного треугольника равна 90 градусам. 2) существуют три прямые, которые проходят через одну точку. 3) Диагонали ромба точкой пересечения делятся пополам. 9. Спортивный магазин проводит акцию. Любая футболка стоит 400 рублей. При покупке двух футболок - скидка на вторую футболку 40%. Сколько рублей придется заплатить за покупку двух футболок в период действия акции? 10. У бабушки 25 чашек: 7 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами. Часть 2. 11. Дорога между пунктами А и В состоит из подъема и спуска, а ее длина равна 22 км. Турист прошел путь из А в В за 8 часов, из которых спуск занял 3 часа. С какой скоростью турист шел на спуске, если его скорость на подъеме меньше скорости на спуске на 2 км/ч? 12. Биссектрисы углов А и В трапеции АВСD с основаниями AD и ВС пересекаются в точке К. Докажите, что точка К равноудалена от прямых АВ, ВС и AD. Вариант 2 Часть 1. Найдите значение выражения Решите уравнение: Ответ_________________. Найдите значение выражения: Ответ ___________________ Установите соответствие между графиками и их функциями: 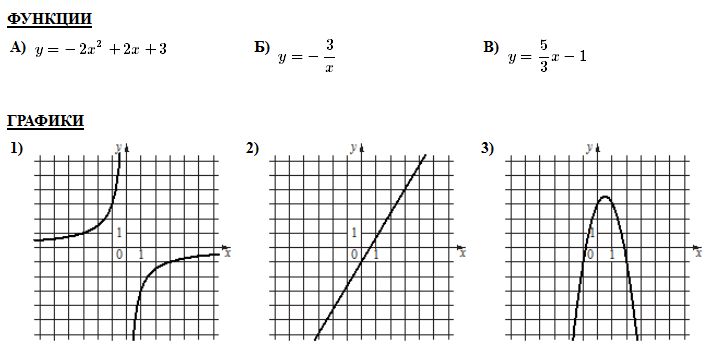 Ответ _________________. 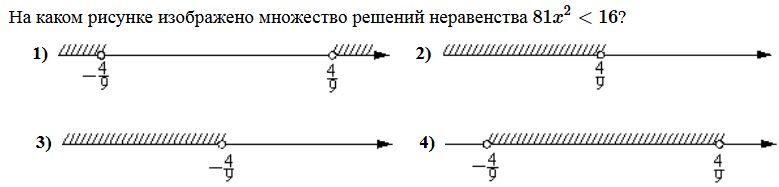 Н  айдите угол айдите угол Н 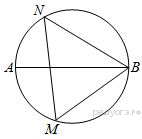 а окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA = 38°. Найдите угол NMB. Ответ дайте в градусах. а окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA = 38°. Найдите угол NMB. Ответ дайте в градусах.Какие из следующих утверждений верны? 1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой. 2) Если диагонали параллелограмма равны, то он является ромбом. 3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу. В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов. Городской бюджет составляет 45 млн. р., а расходы на одну из его статей составили 12,5%. Сколько рублей потрачено на эту статью бюджета? В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из Норвегии или Швеции. Часть 2 Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 180 км. Отдохнув, он отправился обратно в А, увеличив скорость на 5 км/ч. По пути он сделал остановку на 3 часа, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Биссектрисы углов B и C параллелограмма ABCD пересекаются в точке M , лежащей на стороне AD . Докажите, что M — середина AD . Вариант 3 Часть 1 . Найдите значение выражения Решите уравнение: Найдите значение выражения:: Установите соответствие между графиками и их функциями:
Вариант 4 Часть 1 1. Найдите значение выражения Решите уравнение: Найдите значение выражения: Установите соответствие между графиками и их функциями:
Н 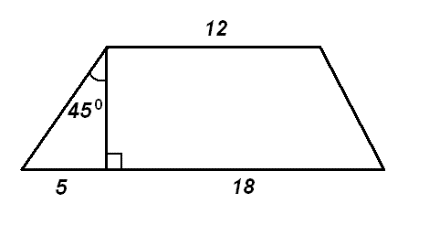 айдите площадь трапеции, изображённой на рисунке. айдите площадь трапеции, изображённой на рисунке.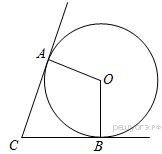 В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах. Какие из следующих утверждений верны? 1) В параллелограмме есть два равных угла. 2) Любая биссектриса равнобедренного треугольника является его медианой. 3) Площадь прямоугольного треугольника равна произведению длин его катетов. В ответ запишите номер выбранного утверждения. Ответ: ___________________________. Семья из трёх человек едет из Санкт-Петербурга в Вологду. Можно ехать поездом, а можно на своей машине. Билет на поезд на одного человека стоит 830 рублей. Автомобиль расходует 10 литров бензина на 100 километров пути, расстояние по шоссе равно 700 км, а цена бензина 19 руб. за литр. Какая поездка (поездом или машиной) обойдётся дешевле? В ответ напишите, сколько рублей она будет стоить. В закрытую коробку помещены 20 шаров: 8 из них – белые, 5 – чёрные, остальные – красные. Какова вероятность того, что, вытаскивая шары из коробки вслепую, первым мы извлечём из неё красный шар? Часть 2 Два велосипедиста одновременно отправляются в 140-километровый пробег. Первый едет со скоростью на 14 км/ч большей, чем второй, и прибывает к финишу на 5 часов раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым. В выпуклом четырёхугольнике ABCD углы CDB и CAB равны. Докажите, что углы BCA и BDA также равны. Вариант 5 Часть 1 Найдите значение выражения: Решите уравнение: Найдите значение выражения: 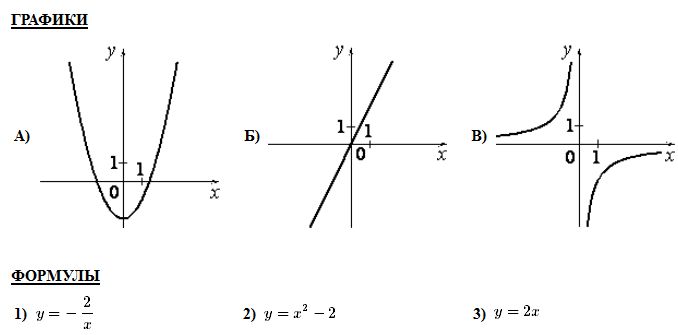
Вариант 6 |