Газовые циклы. Методические указания к расчетнографическим работам для студентов iiiii курсов фла

• Название: Методические указания к расчетнографическим работам для студентов iiiii курсов фла
• Анкор: Газовые циклы
• Дата: 21.05.2022
• Размер: 1.94 Mb.
• Имя файла: 3319_Gazovye_tsikly_RGZ (2).doc
• Тип: Методические указания; #542219
• страница: 1 из 2

Министерство образования и науки Российской Федерации

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
53 № 3319

Г 135

ГАЗОВЫЕ ЦИКЛЫ

Методические указания
к расчетно-графическим работам
для студентов II–III курсов ФЛА
(специальности 160201, 160202, 150300)
дневного отделения

НОВОСИБИРСК
2007

УДК 533.6(07)

       Г 135


Составители: д-р техн. наук, проф. Ю.В. Дьяченко,

канд. техн. наук, доц. А.С. Захаров

Рецензент канд. техн. наук, доц. В.А. Спарин

Работа подготовлена на кафедре технической теплофизики


 Новосибирский государственный

т ехнический университет, 2007   

1. Параметры состояния

Для определения конкретных физических условий, характеризующих состояние вещества, используют так называемые параметры состояния. Состояние любого вещества можно охарактеризовать тремя внутренними параметрами состояния:  – давление, ;  – температура, ;  – плотность, . Иногда вместо плотности используют обратную величину – удельный объем:

. (1)

Уравнение, связывающее между собой параметры состояния, называется уравнением состояния вещества. Для идеального газа уравнение состояния (уравнение Клапейрона) может быть представлено в следующих видах:

• 
  для 1 кг газа
  

; (2)

• 
  для кг газа
  

, (3)

где  – объем кг газа;  – газовая постоянная данного вещества, .

Изменение всех трех параметров состояния , , графически можно представить в виде термодинамической поверхности (рис. 1, а).

Изменение хотя бы одного параметра состояния приведет к изменению двух остальных параметров состояния в соответствии с уравнением состояния (2). Совокупность изменяющихся параметров состояния вещества называется термодинамическим процессом. Термо­ди­на­ми­ческие процессы подразделяются на равновесные и неравновесные. Равновесными называются процессы, представляющие непрерывную последовательность равновесных состояний вещества, когда все части вещества имеют одинаковые параметры состояния.

Любой реальный процесс в той или иной степени является неравновесным, но степень неравновесности будет тем меньше, чем меньше скорость протекания процесса. Поэтому равновесный процесс является предельным случаем неравновесного процесса, когда скорость протекания процесса стремится к нулю. В дальнейшем под понятием «процесс» будем понимать только равновесный процесс.

Термодинамическая поверхность (рис. 1, а) характеризует поле всех возможных состояний вещества. Процесс перехода от состояния 1 до состояния 2 будет графически изображаться кривой 1-2 на термодинамической поверхности.

В трехмерных координатах графическое представление процессов затруднено, поэтому чаще используют плоские диаграммы состояния. На рис. 1, б представлена проекция процесса 1-2 на плоскость , , на рис. 1, в – на плоскость , и на рис. 1, г – на плоскость , .

Рис. 1. Графическая интерпретация термодинамических
процессов
2. Энергетические характеристики

Полная энергия тела или системы макротел в термодинамике определяется как сумма кинетической, потенциальной и внутренней энергии

. (4)

Кинетическая энергия определяется как

, (5)

где  – масса системы;  – скорость.

Потенциальная энергия определяется положением системы в силовом поле. Внутренняя энергия заключена в самой системе и представляет сумму всех видов движения и взаимодействия частиц, составляющих систему.

Внутренняя энергия складывается из энергии поступательного и вращательного движения молекул, энергии сил сцепления между молекулами, внутримолекулярной, внутриатомной энергии (энергии электронных оболочек) и внутриядерной энергии.

Внутренняя энергия является функцией параметров состояния, в общем виде

. (6)

Изменение внутренней энергии не зависит от процесса изменения состояния, а определяется ее значениями в конечном и начальном состояниях. Изменение внутренней энергии в термодинамическом процессе 1-2

. (7)

Внутренняя энергия является экстенсивной характеристикой вещества, т. е. пропорциональна количеству вещества в системе. Поэтому можно ввести понятие удельной внутренней энергии, т.е. внутренней энергии 1 единицы массы вещества:

. (8)

В системе СИ внутренняя энергия измеряется в джоулях (Дж), удельная внутренняя энергия – джоулях на килограмм .

Термодинамическая система обменивается энергией с окружающей средой в виде работы и теплоты. В общем случае в результате подвода теплоты к телу (или телам, составляющим термодинамическую систему) происходит повышение внутренней энергии тела и при увеличении объема тела совершается работа над окружающей средой. Это положение называется первым законом термодинамики. В дифференциальной форме через удельные характеристики

, (9)

где – элементарное количество теплоты;  – изменение внутренней энергии;  – внешняя работа.

Теплота, подводимая к телу, принимается положительной, отводимая – отрицательной. Работа, совершаемая телом над окружающей средой, принимается положительной, работа, совершаемая окружающей средой над телом – отрицательной.

В отличие от внутренней энергии работа и теплота являются функциями процесса. Работа процесса 1-2 для 1 вещества определяется как

. (10)

Графически работа равна площади под процессом в ( ) диаграмме, рис. 2.

Количество теплоты в процессе 1-2 для 1 кг вещества определяется как

; (11)

аналогично для кг вещества

,

где  – удельная теплоемкость вещества.

Теплоемкостью называется отношение количества теплоты, поглощенной телом в процессе, к изменению его температуры

, (12)

где – элементарное количество теплоты;  – элементарное изменение температуры.

Рис. 2. Работа термодинамического процесса

Рис. 3. Теплота в термодинамическом процессе

Численно удельная теплоемкость равна количеству теплоты, которое нужно подвести к единице количества вещества для нагрева на 1 градус. Массовой теплоемкостью вещества ( ) называется количество тепла, необходимое для нагрева 1 кг вещества на .

Объемной теплоемкостью вещества называется количество тепла, необходимое для нагрева 1 единицы объема на ( ).

Мольной теплоемкостью вещества называется количество тепла, необходимое для нагрева 1 моля на ( , ).

Количество теплоты, отводимой или подводимой к телу, зависит еще от вида процесса. На рис. 3 количество теплоты для нагрева 1 кг вещества от до в термодинамическом процессе 1-2 равно . Если кривая процесса идет круче (процесс 1-2), то для нагрева того же вещества от до будет затрачено количество теплоты больше, .

Следовательно, теплоемкость вещества также будет зависеть от вида процесса и для 1 кг вещества

, (13)

где  – вид процесса.

Для изобарного процесса ,  – теплоемкость изобарного процесса. Для изохорного процесса , – теплоемкость изохорного процесса.

Применительно к идеальному газу эти теплоемкости связаны формулой Майера

. (14)

Теплоемкость зависит от температуры и в ряде случаев очень значительно. Поэтому теплоемкость в соотношении (11) называется средней теплоемкостью в интервале температур и обозначается . Истинная теплоемкость определяется по соотношению (12) и представляет теплоемкость при данной температуре.

Тогда количество теплоты в процессе 1-2 на основании выраже­ния (13)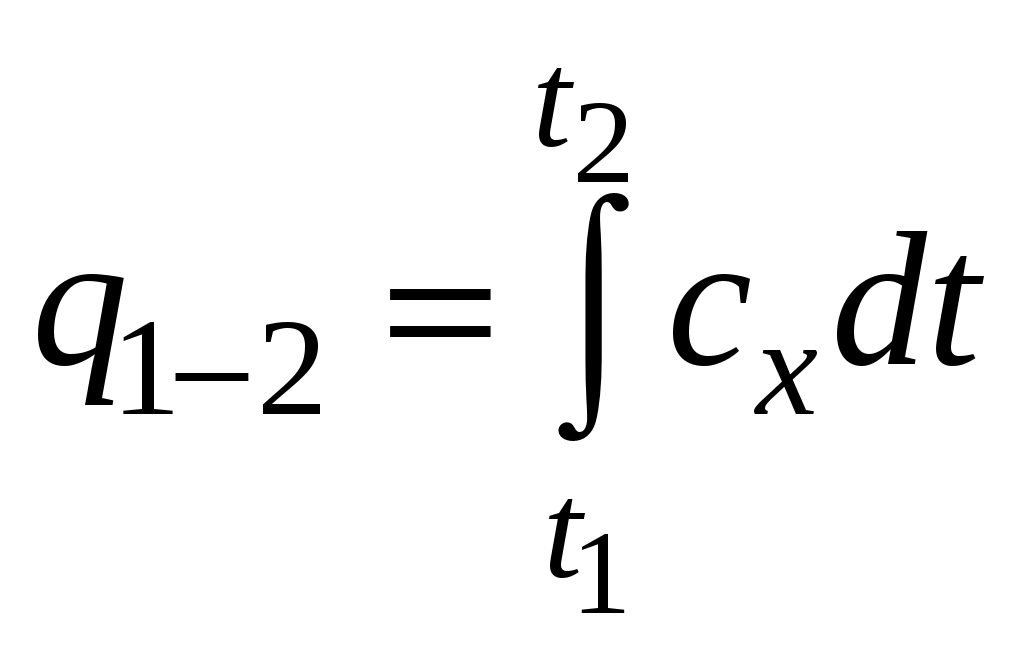

. (15)

Если вместо истинной теплоемкости использовать среднюю теплоемкость в интервале температур ( ), то для 1 кг вещества

. (16)

В термодинамических расчетах очень важную роль играет энтальпия (теплосодержание). Энтальпией называют сумму внутренней энергии системы, и произведение давления на объем системы

. (17)

Как и внутренняя энергия, энтальпия является экстенсивной характеристикой. Для 1 единицы количества вещества

, (18)

где  – удельная энтальпия, .

В соответствии с (16) удельная энтальпия

. (19)

Энтальпия связана с внутренней энергией, поэтому начало отсчета энтальпии связано с началом отсчета внутренней энергии. В точке начала отсчета внутренней энергии , а энтальпия . Энтальпия скомбинирована из величин , являющихся функциями параметров состояния, и, следовательно, тоже являются функцией состояния

. (20)

Изменение энтальпии, как и внутренней энергии, не зависит от процесса, а определяется начальными и конечными значениями .

В математическом анализе доказывается, что если значение криволинейного интеграла не зависит от пути интегрирования, а определяется лишь начальной и конечной точкой интегрирования, то подынтегральное выражение представляет собой полный дифференциал. Так как изменение внутренней энергии и энтальпии не зависит от процесса, а определяется лишь начальными и конечными значениями, то и являются полными дифференциалами параметров состояния и на основании (6), (20)

,

. (21)

Индексы, стоящие у каждой частной производной, показывают, что она взята при постоянном значении величины, обозначенной индексом. Для внутренней энергии характеризует зависимость внутренней энергии от температуры при постоянном объеме, а  – зависимость от объема при постоянной температуре.

Рассмотрим изохорный процесс . На основании  закона термодинамики (9), так как работа расширения , для 1 кг вещества

, (22)

т.е. в изохорном процессе теплота, подводимая к системе, расходуется только на изменение внутренней энергии. Теплоемкость вещества в этом процессе в соответствии с (13)

, (23)

так как мы рассматриваем частный процесс при .

Теплоемкость характеризует скорость изменения внутренней энергии от температуры в изохорном процессе. С учетом (23) выражение для полного дифференциала внутренней энергии будет иметь вид

. (24)

На основании закона Джоуля, для идеального газа

. (25)

Тогда из (24) для идеального газа

, (26)

т.е. внутренняя энергия зависит только от температуры.

Для реального газа внутренняя энергия зависит еще и от объема.

Рассмотрим процесс с . Поскольку работа расширения

, (27)

уравнение закона термодинамики будет

. (28)

На основании преобразования Лежандра

, (29)

тогда

, (30)

или

. (31)

Сумма представляет собой энтальпию, поэтому

, (32)

а так как процесс изобарный , то

, (33)

т.е. в этом процессе все подводимое тепло расходуется только на изменение энтальпии системы. Теплоемкость вещества в изобарном процессе

. (34)

На основании (34) теплоемкость при постоянном давлении характеризует скорость изменения энтальпии от температуры. С учетом (34) выражение для полного дифференциала энтальпии будет иметь вид

. (35)

Для идеального газа частная производная

, (36)

поэтому энтальпия идеального газа не зависит от давления, а так же, как и внутренняя энергия, определяется только температурой

. (37)

Теплота и работа зависят от процесса изменения состояния, поэтому полными дифференциалами не являются и представляют просто бесконечное малое количество тепла и работы.