Множества. Множества. Действительные числа. 13. 1 Основные понятия

• Название: Множества. Действительные числа. 13. 1 Основные понятия
• Дата: 11.01.2019
• Размер: 0.58 Mb.
• Имя файла: Множества.docx
• Тип: Документы; #63296

1. 
   Множества. Действительные числа.
   

13.1 Основные понятия

Под множеством понимают совокупность (собрание, класс, семейство...) некоторых объектов, объединенных по какому-либо признаку. Объекты, из которых состоит множество, называются его элементами. Множества принято обозначать заглавными буквами латинского алфавита А, В,..., X, Y,..., а их элементы — малыми буквами a, b,... ...,х,у,...

Если элемент х принадлежит множеству X, то записывают х X; запись хХ или х X означает, что элемент х не принадлежит множеству X.

Множество, не содержащее ни одного элемента, называется пустым, обозначается символом Ø.

Элементы множества записывают в фигурных скобках, внутри которых они перечислены (если это возможно), либо указано общее свойство, которым обладают все элементы данного множества.

Например, запись А={1,3,15} означает, что множество А состоит из трех чисел 1, 3 и 15; запись А={х:0≤х≤2} означает, что множество А состоит из всех действительных (если не оговорено иное) чисел, удовлетворяющих неравенству 0 ≤ х ≤ 2.

Множество А называется подмножеством множества В, если каждый элемент множества А является элементом множества В. Символически это обозначают так АВ («А включено в В») или ВА («множество В включает в себя множество А»).

Объединением (или суммой) множеств A и В называется множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из этих множеств. Объединение (сумму) множеств обозначают AUВ (или А+В).

Пересечением (или произведением) множеств А и В называется множество, состоящее из элементов, каждый из которых принадлежит множеству А и множеству В. Пересечение (произведение) множеств обозначают А∩В (или А*В). Кратко можно записать А∩В={х:хєА и хєВ}

В дальнейшем для сокращения записей будем использовать некоторые простейшие логические символы:

Α   ß — означает «из предложения α следует предложение ß»;

Α  ß — «предложения α и ß равносильны», т. е. из α следует ß и из ß следует α;

 — означает «для любого», «для всякого»;

 — «существует», «найдется»;

: — «имеет место», «такое что»;

→ — «соответствие».

Числовые множества. Множество действительных чисел

Множества, элементами которых являются числа, называются числовыми. Примерами числовых множеств являются:

N={1; 2; 3; ...; n; ... } — множество натуральных чисел;

Zo={0; 1; 2; ...; n; ... } — множество целых неотрицательных чисел;

Z={0; ±1; ±2; ...; ±n; ...} — множество целых чисел;

Множество R содержит рациональные и иррациональные числа. Всякое рациональное число выражается или конечной десятичной дробью или бесконечной периодической дробью. Так, 1/2= 0,5 (= 0,500...), 1/3=0,333... — рациональные числа.

Действительные числа, не являющиеся рациональными, называются иррационалъными.

Множество R действительных чисел обладает следующими свойствами.

1. Оно упорядоченное: для любых двух различных чисел α и b имеет место одно из двух соотношений а
2. Множество R плотное: между любыми двумя различными числами a и b содержится бесконечное множество действительных чисел х, т. е. чисел, удовлетворяющих неравенству a<х
3. Множество R непрерывное.

Свойство непрерывности позволяет установить взаимно-однозначное соответствие между множеством всех действительных чисел и множеством всех точек прямой

2. 
   Функция. Свойства.
   

Пусть даны два непустых множества Х и У. Соответствие f, которое каждому элементу х Е Х сопоставляет один и только один

элемент у Е У, называется функцией и записывается у = f ( х), х Е Х

или f : Х --+ У.

Пусть задана функция ƒ : X→Y.

Если элементами множеств X и Y являются действительные числа (т. е. X R и Y R), то функцию ƒ называют числовой функцией. В дальнейшем будем изучать (как правило) числовые функции, для краткости будем именовать их просто функциями и записывать у=ƒ(х).

Переменная х называется при этом аргументом или независимой переменной, а у — функцией или зависимой переменной (от х).

Графиком функции у=(х) называется множество всех точек плоскости Оху, для каждой на которых х является значением аргумента, а у — соответствующим значением функции.

Наиболее часто встречаются три способа задания функции: аналитический, табличный, графический.

Аналитический способ: функция задается в виде одной или нескольких формул или уравнений.

Графический способ: задается график функции.

Табличный способ: функция задается таблицей ряда значений аргумента и соответствующих значений функции. Например, известные таблицы значений тригонометрических функций, логарифмические таблицы.

1.Четность и нечетность. Функция f(x) называется четной, если ее значения симметричны относительно оси OY, т.е. f(-x) = f(x). Функция f(x) называется нечетной, если  ее значение изменяется на противоположное при изменении переменной х на -х , т.е. f(-x) = -f(x). В противном случае функция называется функцией общего вида.

   2.Монотонность.  Пусть функция у=ƒ(х) определена на множестве D и пусть D ₁єD. Если для любых значений х ₁;x₂єD₁ аргументов из неравенства x₁₂ вытекает неравенство: ƒ(x ₁)<ƒ(х₂), то функция называется возрастающей на множестве D ₁; f(x₁) ≤ ƒ(х₂), то функция называется неубывающей на множестве D₁; f(x₁)>ƒ(х₂), то функция называется убывающей на множестве D₁; ƒ(х₁)≥ƒ(x₂), то функция называется невозрастающей на множестве D₁.

   3.Периодичность. Если значение функции f(x) повторяется через определенный период Т, то функция называется периодической с периодом  Т ≠ 0 , т.е. f(x + T) = f(x). В противном случае непериодической.

   4. Ограниченность. Функция f (x) называется ограниченной на промежутке Х, если существует такое положительное число М > 0 , что для любого x, принадлежащего промежутку Х, | f (x) | < M. В противном случае функция называется неограниченной.

14.5 Сложная функция

Пусть функция у=ƒ(u) определена на множестве D, а функция u= φ(х) на множестве D₁, причем для  x D₁ соответствующее значение u=φ(х) є D. Тогда на множестве D ₁определена функция u=ƒ(φ(х)), которая называется сложной функцией от х (или суперпозицией заданных функций, или функцией от функции).

Переменную u=φ(х) называют промежуточным аргументом сложной функции.

Например, функция у=sin2x есть суперпозиция двух функций у=sinu и u=2х. Сложная функция может иметь несколько промежуточных аргументов.

Обратная функция

Пусть задана функция у=ƒ(х) с областью определения D и множеством значений Е. Если каждому значению уєЕ соответствует единственное значение хєD, то определена функция х=φ(у) с областью определения Е и множеством значений D

Такая функция φ(у)  называется  обратной к функции ƒ(х) и записывается в следующем виде: х=j(y)=f^-1(y)

Основные элементарные функции и их графики

Основными элементарными функциями называют следующие функции.

1) Показательная функция у=a^х,a>0, а ≠ 1. На рис. 104 показаны графики показательных функций, соответствующие различным основаниям степени.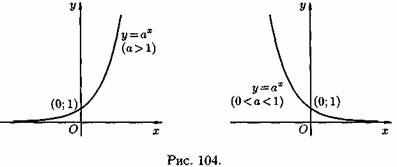



2) Степенная функция у=х^α, αєR. Примеры графиков степенных функций, соответствующих различным показателям степени, предоставлены на рисунках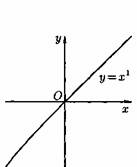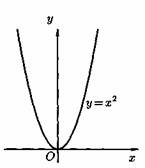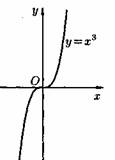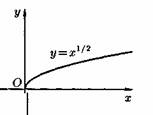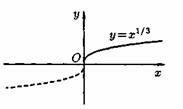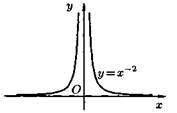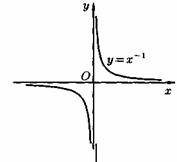



3)Логарифмическая функция y=log_ax, a>0,a≠1;Графики логарифмических функций, соответствующие различным основаниям, показаны на рис. 106.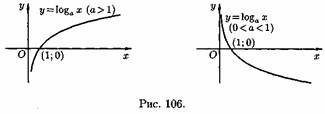



4) Тригонометрические функции у=sinx, у=cosx, у=tgх, у=ctgx; Графики тригонометрических функций имеют вид, показанный на рис. 107.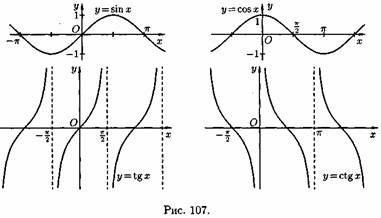



5) Обратные тригонометрические функции у=arcsinx, у=arccosх, у=arctgx, у=arcctgx. На рис. 108 показаны графики обратных тригонометрических функций.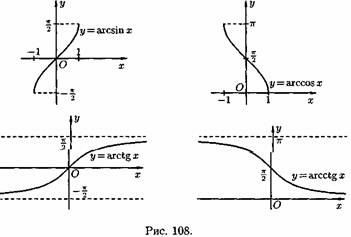



3. Числовая последовательность. Свойства.

Под числовой последовательностью х₁, х₂, x₃,..., х_n... понимается функция

x_n=f(n)   (15.1)

заданная на множестве N натуральных чисел. Кратко последовательность обозначается в виде {х_n} или х_n, nєN. Число x₁ называется первым членом (элементом) последовательности, х₂ — вторым,..., хn — общим или n-м членом последовательности.

Чаще всего последовательность задается формулой его общего члена. Формула (15.1) позволяет вычислить любой член последовательности по номеру , по ней можно сразу вычислить любой член последовательности. Так, равенства



задают соответственно последовательности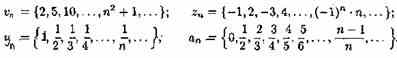



Последовательность {х_n} называется ограниченной, если существует такое число М>0, что для любого nєN выполняется неравенство

|х_n|≤М.

В противном случае последовательность называется неограниченной. Легко видеть, что последовательности у_n и u_n ограничены, а ν_n и z_n — неограничены.

Последовательность {х_n} называется возрастающей (неубывающей), если для любого п выполняется неравенство a_n+1>a_n  (a_n+1≥а_n). Аналогично определяется убывающая (невозрастающая) последовательность.

Все эти последовательности называются монотонными последовательностями. Последовательности v_n, y_n, u_n монотонные, a z_n — не монотонная.

Если все элементы последовательности {х_n} равны одному и тому же числу с, то ее называют постоянной.

4. Предел числовой последовательности. Свойства сходящихся последовательностей.

Можно заметить, что члены последовательности u_n неограниченно приближаются к числу 1. В этом случае говорят, что последовательность u_n, nєN стремится к пределу 1.

Число α называется пределом последовательности (х_n), если для любого положительного числа ε найдется такое натуральное число N, что при всех n>N выполняется неравенство

|х_n-α|<ε                                             (15.2)

В этом случае пишут
  и говорят, что последовательность {х_n} (или переменная х_n, пробегающая последовательность x₁, x₂, х₃,...) имеет предел, равный числу α (или х_nстремится к α). Говорят также, что последовательность сходится к а.

Коротко определение предела можно записать так:


Пример (15.1): 

x_n=f(n)                                         (15.1)

Заметим, что число N зависит от ε. Так, если ε =3/26, то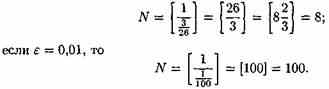



Поэтому иногда записывают N = N(ε ).

Выясним геометрический смысл определения предела последовательности.

Неравенство (15.2) равносильно неравенствам —ε<х_n-a<ε или a-ε<х_n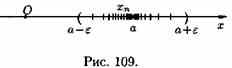


Поэтому определение предела последовательности геометрически можно сформулировать так: число a называется пределом последовательности {x_n}, если для любой ε-окресности точки a найдётся натуральное число N, что все значения хn, для которых n>N, попадут в ε-окрестность точки a (см. рис. 109).

Ясно, что чем меньше ε, тем больше число N, но в любом случае внутри ε-окрестности точки a находится бесконечное число членов последовательности, а вне ее может быть лишь конечное их число.

Отсюда следует, что сходящаяся  последовательность  имеет только один предел.Последовательность, не имеющая предела, называется расходящейся. Таковой является, например, последовательность v_n (см.5.1).

Постоянная последовательность х_n=с, n є N имеет предел, равный числу с, т. е. lim с = с. Действительно, для ε>0 при всех натуральных n выполняется неравенство (15.2).  Имеем |x_n-c|=|c-c|=0< ε.

5. Бесконечно малые и бесконечно большие последовательности. Число е.

Бесконечно большие последовательности







на основании теоремы Вейерштрасса последовательность имеет предел, обозначаемый обычно буквой е:



Число е называют неперовым числом. Число е иррациональное, его приближенное значение зэавно 2,72 {е=2,718281828459045..). Число е принято за основание натуральных логарифмов: логарифм по основанию е называется натуральным логарифмом и обозначается ln(x), т. е. Ln(x)=log_ex. Найдем связь между натуральным и десятичным логарифмами. По определению логарифма имеем х=е^ln(x). Прологарифмируем обе части равенства по основанию 10:



Пользуясь десятичными  логарифмами,  находим  lge ≈ 0,4343.   Значит, lgx ≈ 0,4343•ln(х). Из этой формулы следует, что ln(x) ≈ 1/0.4343 lg(x),  т. е. Ln(х) ≈ 2,3026 lgx. Полученные формулы дают связь между натуральными и десятичными логарифмами.

6. Предел функции в точке. Односторонние пределы. Предел функции при x→∞

Пусть функция у=ƒ (х) определена в некоторой окрестности точки х_о, кроме, быть может, самой точки х_о.

Сформулируем два, эквивалентных между собой, определения предела функции в точке.

Определение 1 (на «языке последовательностей», или по Гейне).

Число А называется пределом функции у=ƒ(х) в топке x₀ (или при х х_о), если для любой последовательности допустимых значений аргумента x_n, n є N (x_nx₀), сходящейся к х_опоследовательность соответствующих значений функции ƒ(х_n), n є N, сходится к числу А



В этом случае пишут       
или ƒ(х)—>А при х→х_о. Геометрический смысл предела функции: означает, что для всех точек х, достаточно близких к точке х_о, соответствующие значения функции как угодно мало отличаются от числа А.

Определение 2 (на «языке ε», или по Коши).

Число А называется пределом функции в точке х_о (или при х→х_о), если для любого положительного ε найдется такое положительное число δ, что для все хх_о, удовлетворяющих неравенству |х-х_о|<δ, выполняется неравенство |ƒ(х)-А|<ε.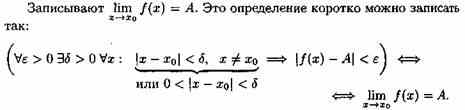



Геометрический смысл предела функции:



если для любой ε-окрестности точки А найдется такая δ-окрестность точки х_о, что для всех ххо из етой  δ-окрестность соответствующие значения функции ƒ(х) лежат в ε-окрестности точки А

   определении   предела   функции считается, что х стремится к x₀ любым способом: оставаясь меньшим, чем x₀ (слева от х₀), большим, чем х_о (справа от х_о), или колеблясь около точки x₀.

Бывают случаи, когда способ приближения аргумента х к х_о существенно влияет на значение придела  функции. Поэтому вводят понятия односторонних пределов.

Число А₁ называется пределом функции у=ƒ(х) слева в точке х_о, если для любого число ε>0 существует число δ=δ(ε)> 0 такое, что при х є (х₀-δ;x_o), выполняется неравенство |ƒ(х)-А|<ε. Предел слева записывают так: limƒ(х)=А при х–>х₀-0 или коротко: ƒ(х_о-0)=А₁(обозначение Дирихле) (см. рис. 111).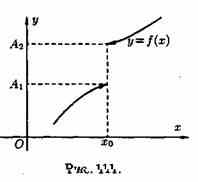



Аналогично определяется предел функции справа, запишем его с помощью символов: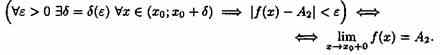



Коротко предел справа обозначают ƒ(х_о+0)=А.

Пределы функции слева и справа называются односторонними пределами. Очевидно, если существует  , то существуют и оба односторонних предела, причем А=А₁=А₂.

Справедливо и обратное утверждение: если существуют оба предела ƒ(х₀-0) и ƒ(х₀+0) и они равны, то существует предел  и А=ƒ(х₀-0).

Если же А₁А₂, то етот придел не существует.

Предел функции при х  ∞

Пусть функция у=ƒ(х) определена в промежутке (-∞;∞). Число А называется пределом функции ƒ(х) при х→∞, если для любого положительного числа ε существует такое число М=М()>0, что при всех х, удовлетворяющих неравенству |х|>М выполняется неравенство |ƒ(х)-А|<ε. Коротко это определение можно записать так:





Геометрический смысл этого определения таков: для ε>0   М>0, что при х є(-∞; -М) или х є(М; +∞) соответствующие значения функции ƒ(х) попадают в ε-окрестность точки А, т. е. точки графика лежат в полосе шириной 2ε, ограниченной прямыми у=А+ε и у=А-ε (см. рис. 112).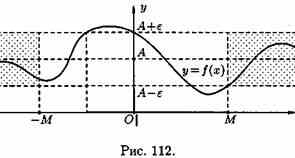



7. Бесконечно большие и бесконечно малые функции. Свойства.

Функция у=ƒ(х) называется бесконечно большой при х→х₀, если для любого числа М>0 существует число δ=δ(М)>0, что для всех х, удовлетворяющих неравенству 0<|х-хо|<δ, выполняется неравенство |ƒ(х)|>М.



Например, функция у=1/(х-2) есть б.б.ф. при х—>2.

Если ƒ(х) стремится к бесконечности при х→х_о и принимает лишь положительные значения, то пишут



если лишь отрицательные значения, то



Функция у=ƒ(х), заданная на всей числовой прямой, называется бесконечно большойпри х→∞, если для любого числа М>0 найдется такое число N=N(M)>0, что при всех х, удовлетворяющих неравенству |х|>N, выполняется неравенство |ƒ(х)|>М. Коротко:

Например, у=2х есть б.б.ф. при х→∞.

Отметим, что если аргумент х, стремясь к бесконечности, принимает лишь натуральные значения, т. е. хєN, то соответствующая б.б.ф. становится бесконечно большой последовательностью. Например, последовательность v_n=n²+1, n є N, является бесконечно большой последовательностью. Очевидно, всякая б.б.ф. в окрестности точки х_о является неограниченной в этой окрестности. Обратное утверждение неверно: неограниченная функция может и не быть б.б.ф. (Например, у=хsinх.)

Однако, если limƒ(х)=А при х→x₀, где А — конечное число, то функция ƒ(х) ограничена в окрестности точки х_о.

Действительно, из определения предела функции следует, что при х→ х₀ выполняется условие |ƒ(х)-А|<ε. Следовательно, А-ε<ƒ(х)<А+ε при х є (х_о-ε; х_о+ε), а это и означает, что функция ƒ (х) ограничена.

Свойства бесконечно больших функций:

1. Произведение б.б.ф. на функцию, предел которой отличен от 0, есть б.б.ф.

2. Сумма б.б.ф. и ограниченной функции есть б.б.ф.

3. Частное от деления б.б.ф. на функцию, имеющую предел, есть б.б.ф.

Функция у=f(х) называется бесконечно малой при х→x_0,если



По определению предела функции равенство (17.1) означает: для любого числа ε>0 найдется число δ>0 такое, что для всех х, удовлетворяющих неравенству 0<|х-x₀|<δ, выполняется неравенство |ƒ(х)|<ε.

Аналогично определяется б.м.ф. при х→х_о+0, х→x₀-0, х→+∞, х→-∞: во всех этих случаях ƒ(х)→0.

Бесконечно малые функции часто называют бесконечно малыми величинами или бесконечно малыми; обозначают обычно греческими буквами α, ß и т. д.

Свойства бесконечно малых функций

1. Алгебраическая сумма конечного числа б.м.ф. есть б.м.ф.

2. Произведение б.м.ф. на ограниченную функцию есть б.м.ф. (в том числе на постоянную или на другую б.м.ф.).

3. Частное от деления б.м.ф., предел которой отличен от 0, есть б.м.ф.

Функция y=f(x)называетсябесконечно большой(илибесконечно большой величиной) при, если. Например,б.б.ф. при, т.к.f(x)→ ∞ илиy=tgxприхб.б.ф.

Аналогично определяется б.б.ф. при х→±∞, + и-.

Если f(x) → ∞ прии принимает лишь положительные значения, то пишут, если лишь отрицательные, то.

8. Основные теоремы о пределах. Признаки существования пределов.

1. Функция не может иметь более одного предела.

2. Предел суммы (разности) двух функций равен сумме (разности) их пределов:



3. Предел произведения двух функций равен произведению их пределов:



4. Постоянный множитель можно выносить за знак предела:

.

5. Предел степени с натуральным показателем равен той же степени предела:



6. Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен 0: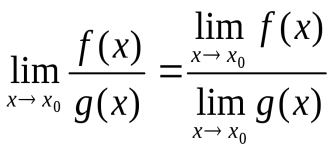

.

7. Если - предел сложной функции.

8. Если в некоторой окрестности точки (или при достаточно большихх)f(x), то.

Признаки существования пределов

Не всякая функция, даже ограниченная, имеет предел. Например, функция у = sin х при х∞ предела не имеет. Во многих вопросах анализа бывает достаточно только убедиться в существовании предела функции. В таких случаях пользуются признаками существования предела.

Теорема 17.10 (о пределе промежуточной функции). Если функция ƒ(х) заключена между двумя функциями φ(х) и g(х), стремящимися к одному и тому же пределу, то она также стремится к этому пределу, т. е. если





то

▼Из равенств (17.6) вытекает, что для любого ε>0 существуют две окрестности δ₁ и δ₂точки х_о, в одной из которых выполняется неравенство |φ(х)-А|<ε, т. е.

 

-ε<φ(х)-А<ε,                                        (17.8)

а в другой |g(х)-А|<ε, т. е.

-ε
 

Пусть δ — меньшее из чисел δ₁ и δ₂. Тогда в δ-окрестности точки x₀ выполняются оба неравенства (17.8) и (17.9).
Из неравенств (17.7) находим, что

φ(x)-A≤f(x)-A≤g(x)-A                         (17.10)

С учетом неравенств (17.8) и (17.9) из неравенства (17.10) следуют неравенства -ε<ƒ(х)-А<ε или |ƒ(х)-А|<ε.
Мы доказали, что

 ε>0  δ>0  x: 0<|х-х₀|<δ  |ƒ(х)-А|<ε, 
то есть lim ƒ(х)=А при х –> x₀.

Теорему 17.10 иногда шутливо называют «принципом двух милиционеров». Роль «милиционеров» играют функции φ(х) и g(х), функция ƒ(х) «следует за милиционерами»▲

  Теорема 17.11(о пределе монотонной функции). Если f(x) монотонна и ограничена при х<х_о или при х>х_о, то существует соответственно ее левый предел или ее правый предел 


Доказательство этой теоремы не приводим.

Следствие 17.6 . Ограниченная монотонная последовательность x_n, nєN, имеет предел.

9. Замечательные пределы и следствия из них.





2 замечательный предел







10. Основные приемы вычисления пределов. Сравнение бесконечно малых функции

При вычислении пределов следует учитывать следующие основные правила:

 

1. Предел суммы (разности) функций равен сумме (разности) пределов слагаемых:

 .

 

2. Предел произведения функций равен произведению пределов сомножителей:

 .

 

3. Предел отношения двух функций равен отношению пределов этих функций: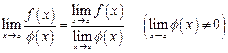

 .

 

4. Постоянный множитель можно выносить за знак предела:

 .

 

5. Предел постоянной равен самой постоянной:

 

 .

6. Для непрерывных функций символы предела и функции можно поменять местами:

 

 .

Сравнение бесконечно малых функций

Как известно, сумма, разность и произведение двух б.м.ф. есть функция бесконечно малая. Отношение же двух б.м.ф. может вести себя различным образом: быть конечным числом, быть бесконечно большой функцией, бесконечно малой или вообще не стремиться ни к какому пределу.

Две б.м.ф. сравниваются между собой с помощью их отношения.

Пусть α=α(х) и ß=ß(х) есть б.м.ф. при х→х_о, т. е.

 и 

1. Если =А 0 (АєR), то α и ß называются бесконечно малыми одного порядка.

2. Если, =0, то α називатся бесконечно малой более высокого порядка , чем ß.

3. Если =∞, то α называется бесконечно малой более низкого порядка, чем ß.

4. Если  не существует, то α и ß называются несравнимыми бесконечно малыми.

Отметим, что таковы же правила сравнения б.м.ф. при х →±∞, х →х₀±0.

<< Пример 18.1<

Сравнить порядок функций α=3х² и  ß=14х²  при х→0

11. Непрерывность функции в точке и ее свойства. Точки разрыва и их классификация.

Пусть функция у=ƒ(х) определена в точке х_о и в некоторой окрестности этой точки. Функция y=f(x) называется непрерывной в точке х₀, если существует предел функции в этой точке и он равен значению функции в этой точке, т. е.



Равенство (19.1) означает выполнение трех условий:

1) функция ƒ (х) определена в точке x₀ и в ее окрестности;

2)  функция ƒ(х) имеет предел при х→х_о;

3)  предел функции в точке х_о равен значению функции в этой точке, т. е. выполняется равенство (19.1).

Так как    то равенство (19.1) можно записать в виде



Это означает, что при нахождении предела непрерывной функции ƒ(х) можно перейти к пределу под знаком функции, то есть β функцию ƒ(х) вместо аргумента х подставить его предельное значение х_о.

Если в точке  функция  не является непрерывной, то эта точка называется точкой разрыва функции.

Классификация точек разрыва функций

1. 
   Устранимый разрыв.
   

Точка а называется точкой устранимого разрыва функции , если предел функции в этой точке существует, но в точке а функциялибо не определена, либо ее значениене равно пределу в этой точке

2. 
   Разрыв первого рода.
   

Точка а называется точкой разрыва первого рода функции , если в этой точке функция имеет конечные, но не равные друг другу левый и правый пределы.

3. 
   Разрыв второго рода.
   

Точка а называется точкой разрыва второго рода функции Точка а называется точкой устранимого разрыва функции , если в этой точке функция не имеет по крайней мере одного из односторонних пределов или хотя бы один из односторонних пределов бесконечен.

12. Свойства функций непрерывных на отрезке.

Свойства функций, непрерывных на отрезке

• 
  Функция называетсянепрерывной на отрезке , если она непрерывна в каждой точке этого отрезка.
  

Свойства функций, непрерывных на отрезке

1. Ограниченность непрерывной функции.

Если функция непрерывна на отрезке, то она ограничена на этом отрезке.

Это означает, что существует такое число , что для всех точекна отрезкевыполняется неравенство.

2. Существование наибольшего и наименьшего значений функции.

Если функция непрерывна на отрезке, то она достигает на этом отрезке как наименьшего, так и наибольшегосвоих значений.

То есть найдутся точки итакие, что

и