Множества. Подмножества.. Дистанционное обучение. Тема «Множество целых чисел. Подмножеств. Множество целых чисел. Подмножества.
 Скачать 246.01 Kb. Скачать 246.01 Kb.
|
|
Тема: «Множество целых чисел. Подмножества.» Тут затеи, и задачи, Игры, шутки, всё для вас! Я желаю всем удачи - За работу, в добрый час! 1.Вводная беседа: До сих пор на уроках математики мы рассматривали натуральные и дробные числа. Какие числа называются натуральными? - Это числа, используемые при счете предметов. Сколько их можете сказать? - бесконечно много. Ноль является натуральным числом? Почему? -нет. С помощью нуля нельзя сосчитать предметы. -Для чего нужны дробные числа? -Мы не только считаем предметы, но части некоторых величин. Какие дроби вы знаете? - Обыкновенные и десятичные. Вы теперь знаете, что числа могут быть положительными и отрицательными, натуральные + им противоположные + нуль – это целые числа. 2. Изучение нового материала: Введем понятие множества: Множество – это количество предметов или чисел, обладающих общими свойствами. Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе. В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A1, A2 и т. д. Объекты множества называются элементами множества и записываются рядом в фигурных скобках { }. Пример: А = {1, 5, 2, 7} – читают множество А состоит из четырех элементов – 1, 5, 2, 7. Принадлежность элементов множеству обозначается знаком – Є. Пример: 5 ЄА – читают элемент «5» принадлежит множеству А. 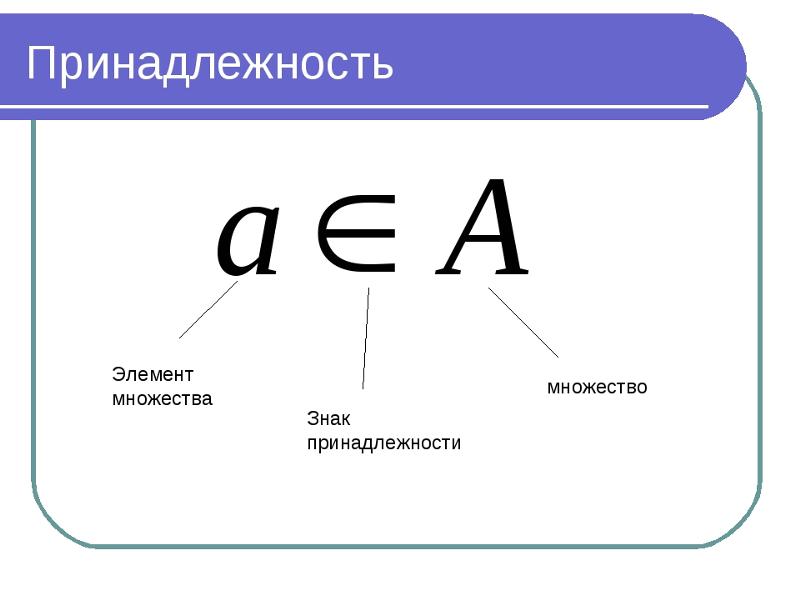 Если два разных множества содержат одинаковые элементы, то одно из них (со всеми своими элементами) является подмножеством другого и обозначается знаком - ⊆. Пример: А = {1, 5, 2, 7} и В = {7, 3, 5, 8, 2, 1} – все элементы А являются элементами множества В, следовательно, А⊆ В. Если множества состоят из одинаковых элементов, их называют равными А = В. В математике рассматривают числовые множества, т.е. его элементами являются числа. Вы сейчас знаете 2 числовых множества: это множество натуральных чисел, его обозначают буквой - N (это числа, используемые при счете предметов) и множество целых чисел, его обозначают буквой – Z (это натуральные + им противоположные + нуль) 3.Рассмотрим их подробнее: 1.Множество натуральных чисел:  2.Множество целых чисел:  Мы видим, что множество N (натуральных чисел) является частью множества Z (целых чисел), т.е. N ⊆ Z. Говорят, что множество N является подмножеством множества Z. Подмножество – это часть какого – либо множества. 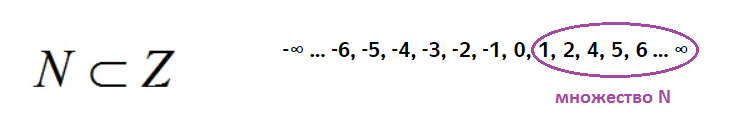 Закрепление: Откройте тетради, запишите тему урока, выполните письменно №44, 43(д – з). 4.Итоги урока: Итак, мы с вами рассмотрели множество натуральных и целых чисел. Натуральные числа — это целые, положительные числа, которые мы используем для подсчета. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13…. Целые числа — это расширенное множество натуральных чисел, которое можно получить, если добавить к ним нуль и противоположные натуральным отрицательные числа. Множество целых чисел обозначают Z. 5. Домашнее задание: выполнить №74, 75, 60(а) |
