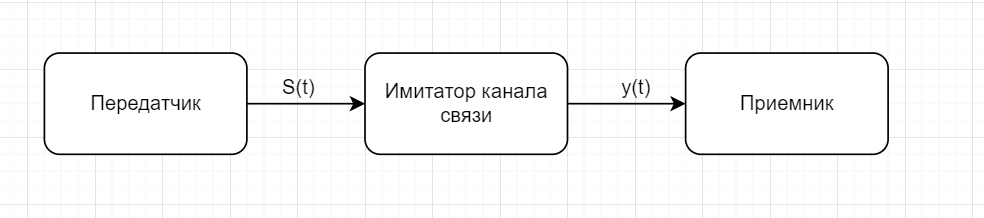
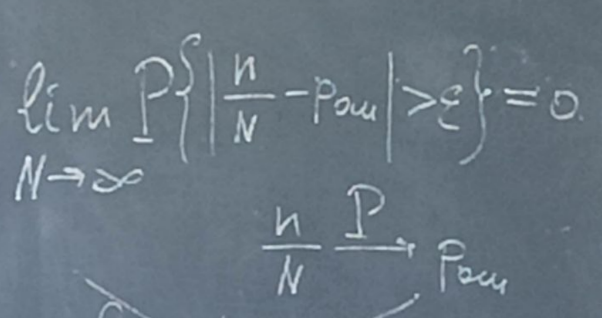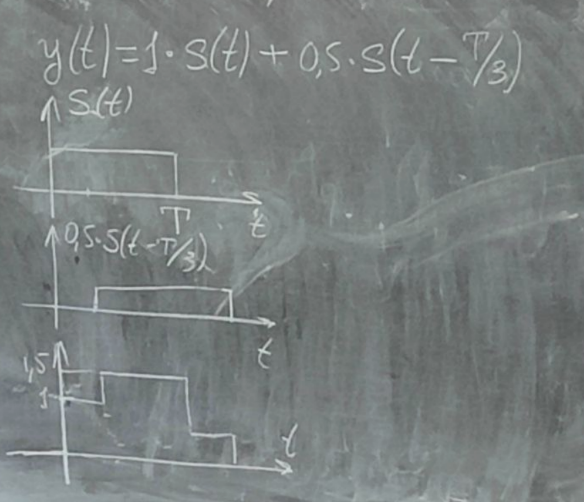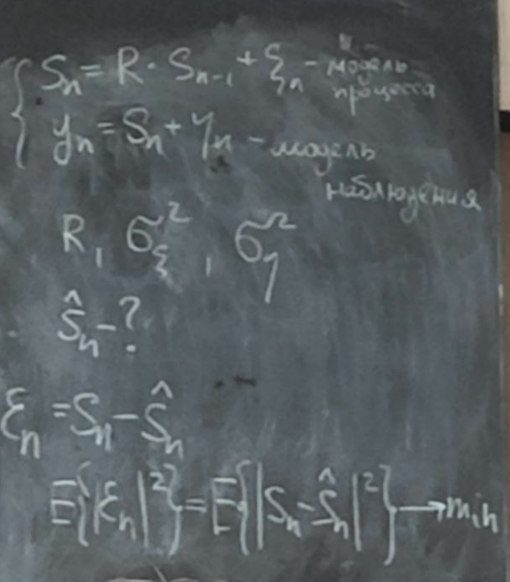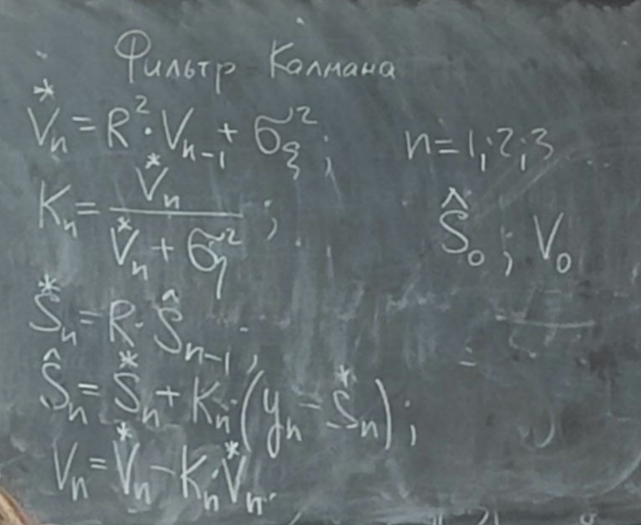лекции Моделирование. лк 1. Модель копия или образец идеального объекта Моделирование замещение объекта его копией

• Название: Модель копия или образец идеального объекта Моделирование замещение объекта его копией
• Анкор: лекции Моделирование
• Дата: 06.02.2023
• Размер: 5.76 Mb.
• Имя файла: лк 1.docx
• Тип: Документы; #923316

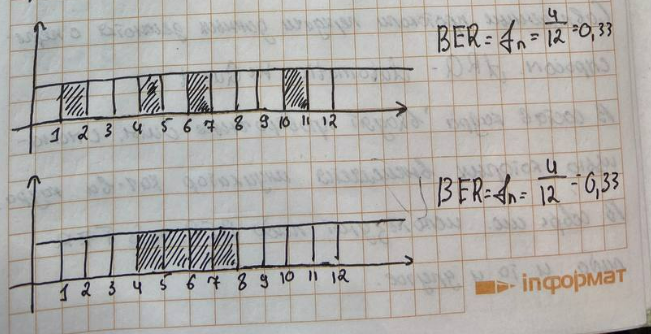
5 сентября

Модель – копия или образец идеального объекта

Моделирование – замещение объекта его копией
При разработке различных технических систем в том числе систем связи пользуются моделированием, и только после проведения моделирование уже проводятся лабораторные эксперименты над реальными системами.

Во многих случаях провести натурный эксперимент либо очень дорого, либо вообще невозможно.

Моделирование на сегодняшний день — это основной метод исследования различных технических систем и процессов.

Модель должна обладать определенным сходством с оригиналом.

При моделировании, свойства идеального объекта делятся на существенные для данной задачи, и несущественные. Модель должна воспроизводить существенные свойства.

Виды моделей

Модели бывают: математические и имитационные, соответственно моделирование бывает: математическое и имитационное.

При математическом моделировании сначала на основе известных физических законов составляются математические уравнения, описывающие реальный объект. Эти уравнения решаются, и на основе решения делается вывод о свойствах этого реального объекта. Из-за сложности решения математических уравнений, математическое моделирование в современных условиях имеет ограниченное применение.

При имитационном моделировании составляются уравнения, описывающие поведение исследуемого объекта. В отличии от математического моделирования эти уравнения решать не требуется. На сегодняшний именно метод имитационного моделирования является основным способом исследования сложных технических систем и процессов.

Классификация моделей

Модели могут быть: детерминированные и стохастические.

Детерминированные модели не учитывают различные случайные факторы.

Стохастические, соответственно, учитываю случайные факторы.

К случайным факторам относится: внешнее случайное воздействие на исследуемый объект, внутренние случайные факторы, старение.

На сегодняшний день более полным методом является стохастическое моделирование, для исследования сложных процессов.

Статические модели и динамические: статические описывают поведение объекта в определенный момент времени, динамические – описывают поведение объекта во времени.

Имитационное моделирование выгодно применять если выполняется хотя бы одно из условий:

• 
  не существует законченно математической постановки задач,
  
• 
  аналитически описать систему очень сложно,
  
• 
  аналитические решения имеются, но их реализация невозможна из-за недостаточной математической подготовки персонала,
  
• 
  необходимо осуществлять наблюдение за процессом в течении определенного времени.
  

При проведении имитационного моделирования требуется контролировать погрешность.

Адекватность модели

Адекватность – степень соответствия модели реальному объекту.

Задача проверки адекватности модели должна решаться в течении всего процесса моделирования.

Недостатки модели:

1. 
   Модель может содержать несущественные переменные.
   
2. 
   Модель может не содержать существенных переменных.
   

Иерархия моделей

Сначала строится самая простая модель, которая учитывает только основные свойства объекта. Это самая простая модель – низшая ступень иерархии. Она обычно не адекватная.

Для того чтобы модель была более точной мы должны учесть большее кол-во свойств реального объекта, и построить более точную модель, но эта модель будет более сложной – 2 уровень иерархии

Надо учесть больше свойств реального объекта, и построить более точную модель, если нас по-прежнему что-то не устраивает.

Этот процесс повторяется, пока нас не будет устраивать степень точности\адекватности, процесс прекращается, когда модель станет недопустимо сложной.

Существуют способы упрощения модели без снижения её адекватности.

Моделирование случайных чисел

Случайное событие – может произойти, а может и нет.

Случайные события характеризуются вероятностями их наступления.

Вероятность случайного события P(A) = [0, 1]

Случайная величина – это величина, значение которой после проведения эксперимента нельзя точно предсказать.

19 сентября

Для генерации случайных величин используются датчики случайных чисел.

Датчик случайных чисел – это специализированная программа, которая генерирует некоторую последовательность чисел по определенному правилу или алгоритму. Причем эта последовательность не является случайной, а является детерминированной.

Гипотеза Лапласова детерминирования – если мы знаем всё про все молекулы во вселенной

Датчик случайной величины должен быть построен таким образом, чтобы свойства детерминированности были такие же как в случайной последовательности. В основных программных пакетах датчики уже созданы, нам нет нужды их программировать.

В матлабе существует датчик rand(1) который формирует детерминированную последовательность, которая равномерно распределена в интервале (0, 1), но мы ее считаем случайной

Формирование случайной величины с равномерным распределением

Каждый раз при повторном запуске x = rand(1); мы будем получать новое значение случайной величины Х которая будет находится между 0 и 1.

Rand(1)

X = (a, b)

Шаг 1 – формируем случайную величину Y имеющюю равномерное распределение в интервале (0, 1)

Шаг 2 – осществляем линейное преобразование величины Y – поулчаем величину X – которая равна = (b – a) * Y + a

Y = rand(1);

X = (b-a)*y + a;

Формирование дискретных двоичных случайных величин

Дискретная случайная величина которая может принимать только два значения называется двоичной или бинарной случайной величиной. В связи информация передается по битам.

Rand(1) – мы модем установить порог в 0.5 и создать такой алгоритм:

X = rand(1);

If (x <= 0.5)

I = 0;

Else

I = 1;

Рассмотрим формирование двоичной случайной величины с НЕравновероятным распределением:

X = rand(1);

If (x <= 0.5)

I = 0;

Else

I = 1;

Формирование дискретных НЕ двоичных случайных величин:

0; 1; 2; 3; 4; 5; 6; 7

Вероятность того. что случайная величина C примет значение G равна 1/8

Сначала формируются двоичные случайные величины ξ0 ξ1 или ξ2. В общем случае формирование дискретных недвоичных случайных величин производится на основе двоичных случайных величин.

Формирование Гауссовской случайной величины

Гауссовская случайная величина относится к непрерывным случайным величинам.



Шумы и помехи в технических системах и в системах связи имеют гауссовское распределение.

Центральная предельная теорема – допустим у нас есть случайные величины x1, x2, x3 … xn и мы можем составить случайную величину которая будет суммой всех этих случайных величин – сумма большого кол-ва случайных величин это случайная величина закон распределения которой приближается к Гауссовскому закону о распределении при увеличении числа членов в сумме. Чем больше n, тем ближе значение величины к гауссовскому распределению.

Условия справедливости центральной предельной теоремы:

1. 
   нужно чтобы эти случайные величины (члены сумма) были между собой слабо зависимы
   
2. 
   среди членов суммы не было доминирующего члена
   

Обычно шумы и помехи в системах связи и в целом информационных системах представляют собой сумму различных случайных воздействий.

T = randn(1); - m = 0, D(x) = 1

Задача формирования гауссовского

Дано: m; d = σ²

Найти: случайную величину X

Шаг 1 – формируем случайную величину Y с распределением m = 0 и σ² = 1

Y = randn(1);

Шаг 2 – делаем линейное преобразование величины Y

X = σ*Y + m

X = sqrt(D)*Y + m

Известен следующий универсальный принцип который используется при формировании случайных величин – сначала формируется случайная величина с неким простым распределением, а затем путем некоторого (обычно линейного) преобразования формируется случайная величина с требуемым более сложным распределением.

Формирования рэлеевской случайной величины

Предположим что X и Y это случайные величины с нулевыми m = 0, и с одинаковыми дисперсиями. σ²_х не зависит от σ²_y.

X = sqrt(D) * randn(1);

Y = sqrt(D) * randn(1);

Z = sqrt(X² + Y²)

Существует огромное количества случайных величин и распределений, для каждой есть свой собственный метод формирования.

06 октября

Формирование случайных векторов

Случайный вектор – совокупность заданного количества заданных случайных величин.

Случайный вектор размерности n – это совокупность из m случайных величин.

На первый взгляд, проблемы никакой нет, и можно сформировать каждый компонент случайного вектора.

Пример: пусть нам надо сформировать случайный вектор гауссовскими компонентами, каждый из которых имеет нулевое средне и единичное дисперсии

X(1) = randn(1);

X(2) = randn(1);

…

X(n) = randn(1);

Можно сделать так

For I = 1:n

X(i) = randn(1);

End;

Такая реализация программы формирования гауссовского случайного вектора неоптимальна с точки зрения времени выполнения программы.

Трансляторы

Транслятор — это такая специальная программа, которая преобразует программу на ЯП высокого уровня, в программу написанную на языке машинных кодов.

Трансляторы бывают двух видов: компиляторы и интерпретаторы.

Компилятор – транслятор, который переводит сразу всю программу на язык машинных кодов, а потом вся программа целиком на машинных кодах целиком исполняется.

Интерпретатор – осуществляет трансляцию в машинные коды построчно, и исполнения тоже построчное. MATLAB – интерпретатор.

Время выполнения программы в среде MATLAB в режиме интерпретатора оказывается во много раз больше, чем при использовании режима компилятора.

X = randn(n, 1); - вектор с числом столбцов n и строк 1

Данная программа формирует гауссовский случайный вектор с независимыми компонентами, каждая из которых имеет нулевое математическое ожидание и единичную дисперсию.

При составлении программ моделирования в системе MATLAB, необходимо всячески избегать циклов. В MATLABе предусмотрено средство векторизации циклов. MATLAB ориентирован на операции с векторами и матрицами.

Пример №1

Сформировать гауссовский случайный вектор с независимыми компонентами, каждый из которых имеет математическое ожидание M и дисперсию равную 1.

σ² = D = 1, m

For I = 1:n

X(i) = randn(1) + m;

End;

X = randn(n, 1) + m; - в данном случае это сложение необычное, оно означает что к каждой компоненте randn прибавляется число m.

Пример 2

Сформировать гауссовскую случайный вектор с независимыми компонентами, каждый из которых имеет свое собственное математическое ожидание единичную дисперсию

m-> = {m1, m2, m3}, σ² = D = 1

for I = 1:n

x(i) = randn(1) + m(i);

end;

после векторизации:

x = randn(n, 1) + m; - m это не число, а вектор. Операция сложения двух векторов.

Пример 3

Сформировать гауссовский случайный вектор с независимыми компонентами, каждый из которых имеет свое собственное математическое ожидание и дисперсию D = σ².

For I = 1:n

X(i) = sqrt(D)*randn(1) + m(i);

End;

После векторизации:

X = sqrt(D)*randn(n, 1) + m; - число умножатся на вектор, тоесть на каждую компоненту вектора. И сложение двух векторов.

Пример 4

Сформировать гауссовский случайный вектор с независимыми компонентами, каждый из которых имеет свое собственное математическое ожидание, и свою собственную дисперсию.

M-> = {m1, m2, m3}, D-> = {D1, D2, D3}

For I = 1:n

X(i) = sqrt(D(i))*randn(1) + m(i);

End;

После векторизации:

X = sqrt(D).*randn(n, 1) + m; - sqrt(D) означает что квадратный корень берется из каждой компоненты вектора D. «.» означает что умножение носит поэлементный характер. Когда два вектора-столбца одинаковой размерности можно перемножить и получить новый вектор-столбец.

Формирование гауссовского случайного вектора с зависимыми компонентами

Зависимость и независимость случайных величин

Допустим есть две случайные величины X и Y. Пара случайных величин называется совокупностью. Для полного описания совокупности двух случайных величин достаточно иметь их совместную плотность распределения p(x, y).

Если есть отдельная случайная величина x, то полная вероятностное описание этой величины дает ее плотность распределения p(x). Аналогично для y – p(y). Если случайные величины x и y независимы то их совместная плотность распределения равно произведению плотностей:

p(x, y) = p(x) * p(y)

Независимость означает, что плотность распределения одной случайной величины не зависит от тех значений, которые принимает другая случайная величина.

Есть две случайные величины X и Y. Между ними можно вычислить коэффициент корреляции –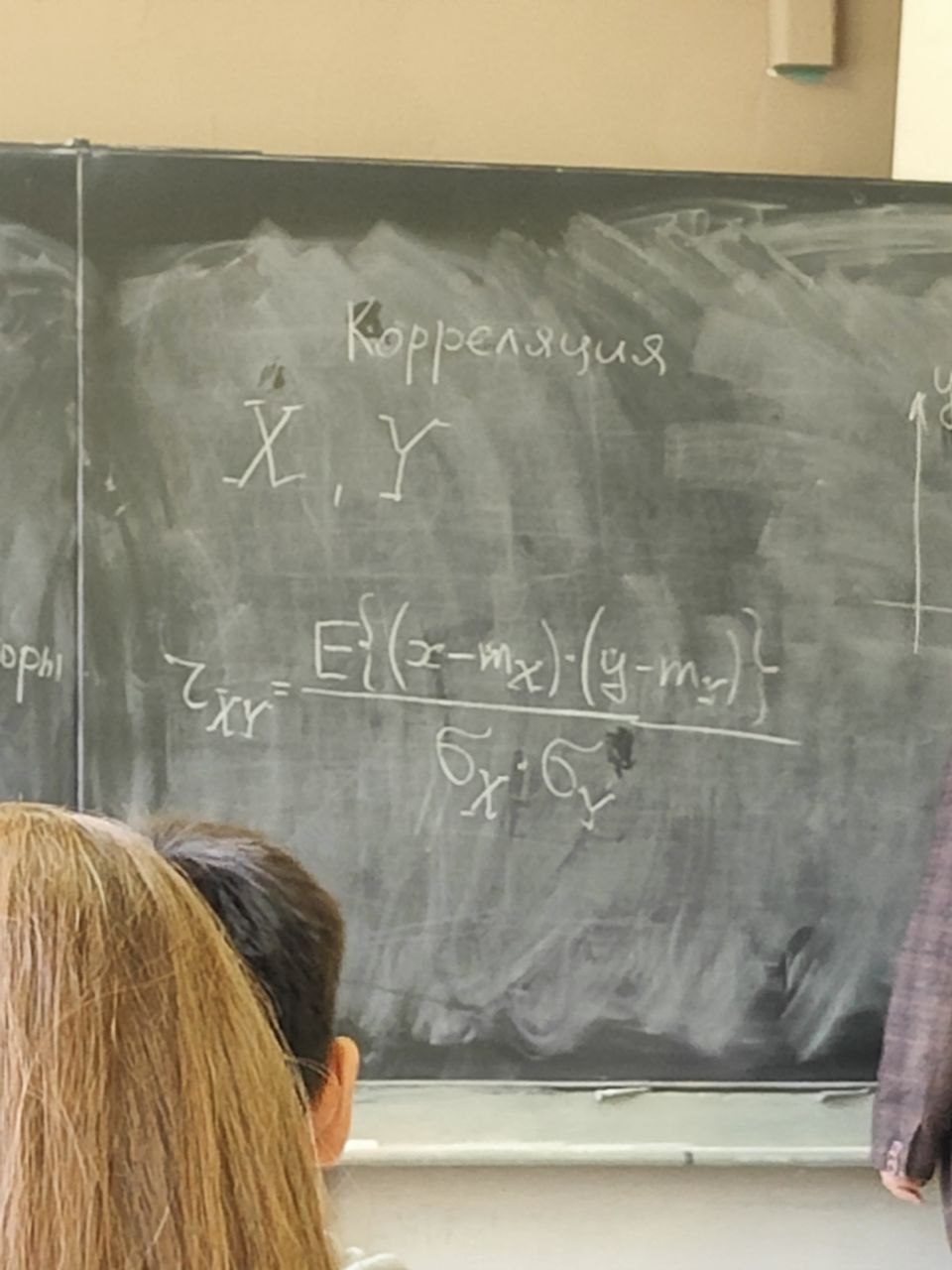



Если случайные величины X и Y независимы, то они не коррелированы, то есть их коэффициент корреляции равен 0.

Если случайные величины X и Y зависимы, то они могут быть как коррелированы, так и некоррелированные.

Корреляция отображает линейную вероятностную зависимость.

Если случайные величины X и Y являются гауссовскими, то для них понятие корреляции и зависимости совпадают. Если случайные величины гауссвские и зависимые, значит, что они коррелированные.

Гауссовский случайный вектор

X-> = {X1, … ,Xn}; m-> = {m1, m2, … ,m_n}

И описывается ковариационный матрицей V.

Если у нас есть компоненты вектора Xi и Xj то мы можем вычислить ковариацию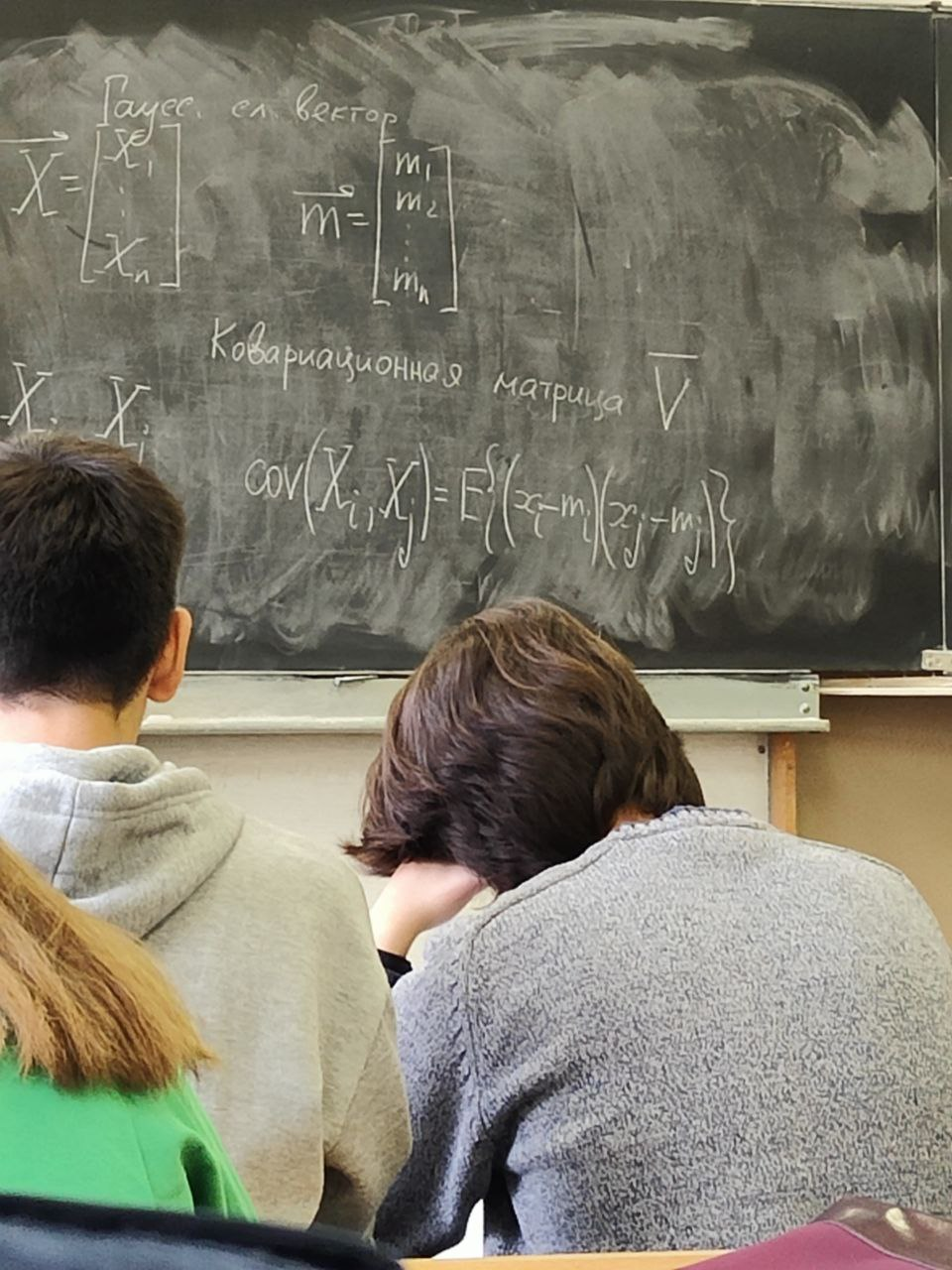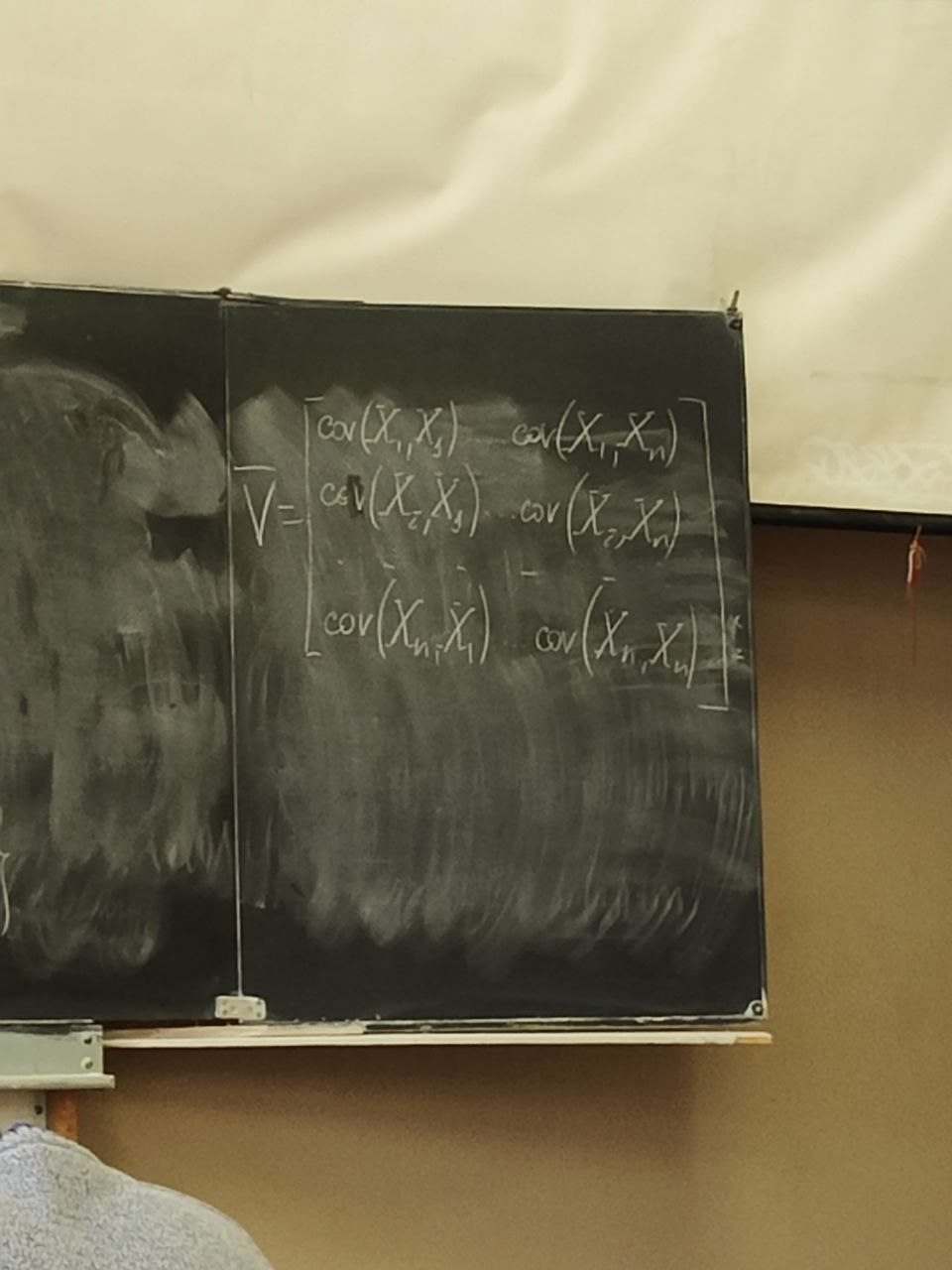





Существует еще одно описание – корреляционная матрица. Она состоит из коэффициентов корреляции.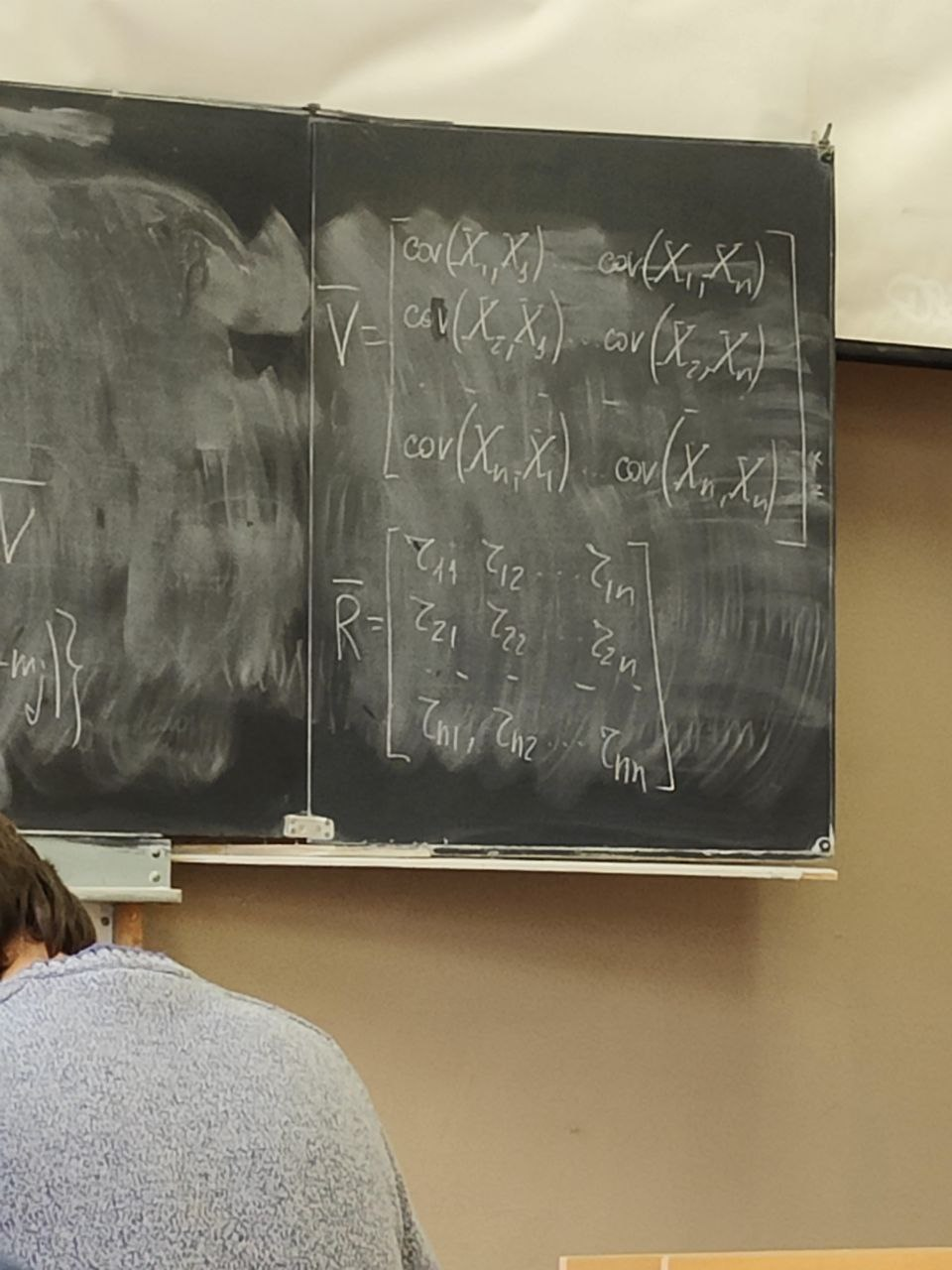



Сам коэффициент корреляции находится в пределах от -1 до 1.

20 октября

Задача

Сформировать гауссовский случайный вектор с заданным вектором математических ожиданий и с заданной корреляционной матрицей.

Свойство корреляционной матрицы

R_ii = 1; коэффициент корреляции случайной величины с самой собой равен 1.

Задача решается в два этапа:

На первом этапе формируется гауссовский случайный вектор y-> с нулевым математическим ожиданием M_y = 0 и корреляционная матрица R_y = 1 которая является единичной матрицей.

Второй этап: формируем наш искомый вектор X ьс помощью линейного преобразования: X-> = T->*Y-> + b->

С заданным m_x и с заданным R_x

Матрица T и вектор b пока неизвестны.

Найти:

Матрицу T и вектор b

Выполним операцию математического ожидания над обеими частями равенства:

M_x = E{T*Y+b} = E{T * Y} + b = T * E{Y} + b = T * 0 + b = b

M_x = b

R_x = E{(X – m_x)*(X-m_x)} = E{(T*Y)*(T*Y)^T}=E{T*Y*T^T*Y^T} =

Поскольку матрица T(тэ большое)– это не случайная матрица, то ее можно вынести за знак усреднения, тогда получаем:

= T*E{Y*Y^T}T^T = T * T^T

R_x = T * T^T – необходимо решить это квадратное матричное уравнение, и найти матрицу Т

Известно, из теории матриц, разложение Холецкого для квадратной матрицы.

R = U * U^T, где U – тоже квадратная матрица, только она верхняя треугольная

Для того чтобы существовало разложение Холецкого, нужно чтобы матрица R была положительно определенной.

Существует алгоритм вычисления разложения Холецкого, который уже реализован в MATLAB. В MATLAB есть функция – T = chol(R); Если функция chol дает ошибку, это значит что разложение Холецкого вычислить невозможно, то задача формирования нашего вектора X тоже не имеет решения. Данная матрица не является корреляционной. Существуют способы определить заранее положительно определенная матрица, или нет. Существуют критерии выяснения того, является ли матрица положительно определенной. Самый известный – критерий Сильвестра. Составим программу для решения задачи:

Y = randn(n, 1);

T = chol(R);

X = T*Y+m;

В данном случае мы снова воспользовались уже известным правилом, которое состоит в то, что мы сначала формируем случайный вектор с простым распределением, а затем делаем его преобразование (в данном случае линейное), и получаем нужный нам вектор со сложным законом распределения.

Моделирование систем связи

В системах связи обычно используются потоки бит для переноса информации, с помощью которых переносится любая информация (речь, видео, аудио, и т.д.

Кодер источника устраняет информационную избыточность – это значит что если в исходном файле символы сильно зависимы, то кодер источника эту зависимость устраняет.

Помехоустойчивый кодер вводит избыточность передаваемых данных, за счет этого на приемной стороне можно исправить некоторые ошибки.

Модулятор нужен для того чтобы приспособить свойства сигнала к свойствам канала связи.

Канал связи – среда распространения сигнала. Это может быть провод, оптоволокно, или просто пространство в случае радиоволн.

В канале связи сигнал подвергается воздействию шумов, помех и искажений.

Принятые комплексные моделированные символы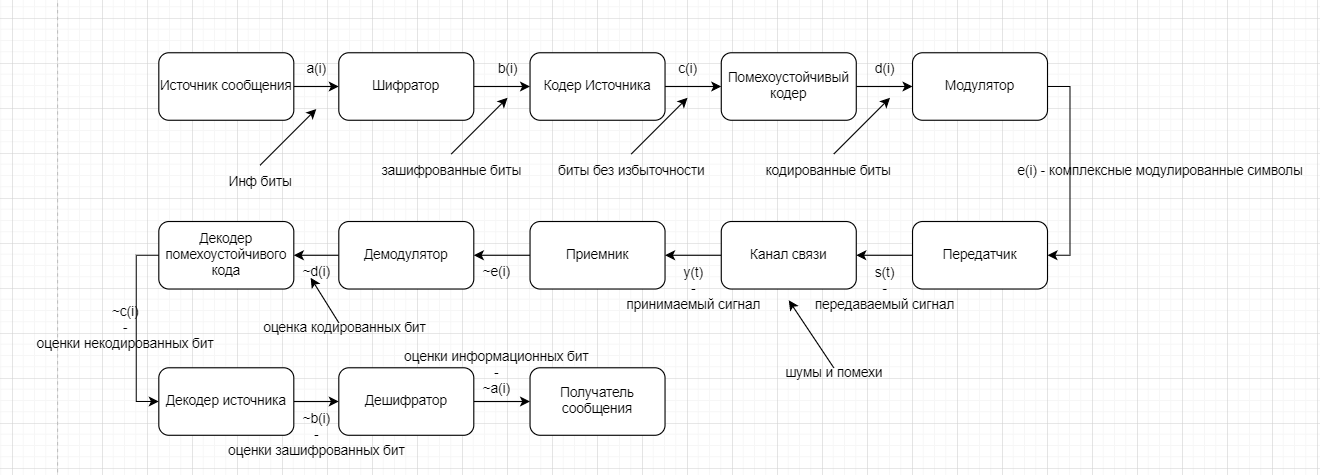



Критерием качества работы системы связи может быть вероятность ошибки на бит.

P{ a_j +- a_j} – вероятность ошибки на бит = p_ош

N – общее число переданных бит

n – число ошибочно принятых бит

n/N = относительная частота (коэффициент появления ошибок)

Если N стремится к бесконечности, то F_n = n/N -> p_ош

Lim(n/N)_{n -> беск} = p_ош - неверно

Сходимость по вероятности означает, что предел вероятности отклонения коэффициента ошибок от вероятности ошибок равен 0.



Надо моделировать таким образом чтобы N > 10.

К сожалению, вероятность ошибки на бит не полностью характеризует качество работы системы



Во многих ситуациях – возникновение блоков ошибок является крайне нежелательным, и это целесообразно учитывать при моделировании системы.

Frame Error Rate - FER

Вся последовательность бит разбивается на группы, которая называется кадрами. Кадр считается принятым правильно, если все его биты приняты правильно (если хотя бы один бит в кадре неправильный – весь кадр неправильный). Если кадр принят ошибочно, традиционно в системах организуется переспрос. Все это реализуется в протоколах сетей, кадр передается заново.

Block Error Rate – BER

03 ноября

Модели каналов связи

В системах связи сигнал, проходящий через канал связи претерпевает искажения, и подвергается воздействию шумов и помех. Для того чтобы достичь высокого качества приема сигнала, система связи должна быть приспособлена к свойствам канала связи, и структура самого сигнала должна учитывать свойства канала связи.

Но для того, чтобы нам это сделать, нам надо знать свойства канала связи.

Свойства канала связи описываются моделью канала связи.

Канал связи имитирует среду распространения сигнала от передатчика к приемнику, и модель канала показывает, как именно искажается сигнал после прохождения через канал связи, и как именно воздействуют помехи.

1. 
   Идеальный канал связи
   

y(t) = s(t)

y(t) – принимаемый сигнал, s(t) – передаваемый сигнал

При идеальной модели канала – ровно тот сигнал, который передавался, ровно он и поступает в приемник. Здесь отсутствуют какие-либо искажения шумы и помехи. Такой канал на практике не существует.

2. 
   Канал связи без замираний с Аддитивным Белым Гауссовским Шумом (АБГШ) (AWGN – Additive White Gaussian Noise)
   

y(t) = s(t) + η(t)

Аддитивный – значит, что шум складывается с сигналом.

Белый – значит, что его спектральная плотность мощности постоянна на всех частотах.

Гауссовский – плотность распределений равномерных значений этого шума является Гауссовским.

Шум – шум.

Сигнал имеет постоянный уровень, замирания не происходит.

Виды шумов и помех в системах связи

1. 
   Тепловой шум приемника
   

Причина этого шума – движения электронов в проводнике. Обычно имеет гауссовское распределение. Его величина зависит от температуры. Как бороться с шумом – охлаждать приемник, желательно до абсолютного нуля (-273 по цельсию). Уменьшить его мы не можем.

2. 
   Внутрисистемные помехи
   

Помехи со стороны других абонентов системы.

3. 
   Межсистемные помехи
   

Помехи со стороны других систем связи.

4. 
   Индустриальные помехи (помехи промышленного происхождения)
   

Существует два способа борьбы с индустриальными помехами:

1. 
   Технический
   

Предприятие мер по борьбе с помехой (подавление). Подавление помехи непосредственно в средстве связи (фильтр например).

Подавление помех в месте их возникновения. – технически сделать можно, но практически – нереально из-за нежелания производителей это делать.

2. 
   Организационный (административный)
   

Принять закон, принять меры по контролю за исполнением этого закона. На международном уровне существует регулирование уровней индустриальных помех. Все государства договорились о допустимом уровне помех.

3. 
   Модель канала связи с замираниями с Аддитивным Белым Гауссовским Шумом (АБГШ) (AWGN – Additive White Gaussian Noise)
   

y(t) = A * s(t) + η(t)

A – случайный коэффициент, случайная величина, может иметь различное распределение. Эта величина показывает коэффициент ослабления сигнала.

В зависимости от распределения существует много разновидностей этой модели. Наиболее потребительная модель – модель с Рэлеевскими замираниями.

Величина А может иметь Рэлеевское распределение, а может и какое-нибудь другое.

4. 
   Нестационарная модель канала связи с замираниями и с Аддитивным Белым Гауссовским Шумом
   

y(t) = A(t) * s(t) + η(t)

Часто встречается на практике.

5. 
   Многолучевые модели канала связи с АБГШ.
   

y(t) = sum^Q_q=1(A_q*s(t – τ_q)) + η(t)

Q – число лучей,

A_q – амплитуда q-того луча

τ_q -

В данной модели имеется прямой луч, и много отраженных лучей. Число отраженных лучей может быть большим. Прямого луча может и не быть



Чем большее число отражений претерпевает сигнал, тем меньше его мощность, и тем больше его задержка. В приёмнике все эти лучи складываются.

Многолучевое распространения радиоволн приводит к существенным искажениям сигнала.



Форма сигнала при прохождении такого, даже двухлучевого канала связи сильно исказилась.

Перед разработчиком системы встает вопрос – какой сигнал s(t) лучше всего передать, чтобы искажения сигнала после прохождения через многолучевой канал, были минимальны. И как принять такой сигнал?

Как выделить из такого искаженного сигнала полезную информацию.



В данном случае здесь есть элементы натурного эксперимента, и элементы моделирования, обычно имитатор канала связи реализуется в виде программной модели, а передатчик и приемник — это реально существующие устройства.

После того, как проведены лабораторные измерения с применением имитатора канала связи, уже проводятся реальные испытания системы на реальном канала связи.

17 ноября

Фильтрация в технических системах

Постановка задачи фильтрации:

y(t) = s(t) + η(t)

S(t) – полезный сигнал

η(t) – шум

y(t) – принимаемый сигнал

Наша задача выделить полезный сигнал.

После того как проведены лабораторные измерения с применением имитатора канала связи проводится реальное испытание системы на реальном канале связи.

Оценка полезного сигнала – некий функционал. В такой постановке задача фильтрации решения не имеет. Для успешного решения задачи фильтрации необходимо задать отличительные признаки сигнала от шума.

y(n) = s(n) + η(n)

Далее будем рассматривать модель наблюдаемого сигнала в дискретном времени. Если шум предполагается белым, то по времени он не коррелирован, а изменения сигнала во времени должны подчиняться какому-то закону.

Охарактеризовать свойства сигнала можно с помощью модели.

Если сигнал имеет модель авторегрессии первого порядка, то на этом основании можно выделить сигнал из смеси с шумом. В данной постановке задача фильтрации все равно не имеет решения.

Для получения решения задачи фильтрации необходимо задать требования точности оценки.

ε(n) – ошибка фильтрации.

Сам сигнал s(n), его оценка s(n) являются случайными процессами. Поэтому ε(n) тоже будет случайным процессом.

ε(n)

Критерием качества фильтрации выберем средний квадрат ошибки фильтрации. Среди всех возможных оценок мы должны выбрать такую оценку, которая дает минимальный средний квадрат ошибки фильтрации.

Решение задачи фильтрации может быть записано в следующем виде.

Мы имеем n отсчетов наблюдаемого сигнала, дальше эти n отчетов мы обрабатываем с помощью функции F, и получаем оценку полезного s(n) сигнала на n-ом шаге фильтрации.

s(n) = F(y1, y2, … ,yn) – не рекуррентная фильтрация

Крупным недостатком не рекуррентной фильтрации является то, что при поступлении нового отсчета наблюдаемого сигнала, оценка s_n выбрасывается, и заного рассчитывается новая оценка s_n+1, что требует большого объема вычислений.

s_n+1 = f(s_n, y_n+1) – рекуррентная фильтрация

При такой фильтрации на каждом шаге предыдущая оценка полезного сигнала не выбрасывается, а модифицируется (пересчитывается) с учетом вновь поступившего нового отсчета наблюдаемого сигнала. Вычислительная сложность алгоритмов не рекуррентной фильтрации гораздо выше, чем вычислительная сложность рекуррентной фильтрации. Обычно в современной технике, и технике связи используется рекуррентная фильтрация.

Решение задачи фильтрации – Фильтр Калмана

Фильтр Калмана относится к классу линейных алгоритмов фильтрации. Линейный алгоритм значит, что модель самого сигнала является линейной.



Обе модели должны быть линейными, а шум возбуждения и шум наблюдения должны быть гауссовскими.



V_n-1 – это дисперсия ошибки фильтрации на n-1 шаге.

*V_n – это дисперсия ошибки предсказания с n-1 шага на n шаг.

K_n – коэффициент усиления фильтра Калмана.

S_n-1 – оценка полезного сигнала на n-1 шаге.

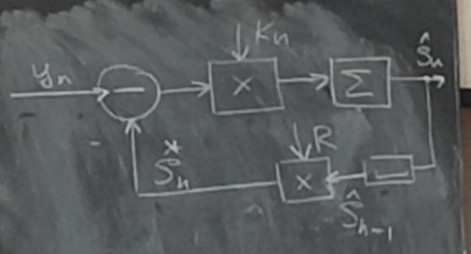
*S_n – экстраполированная (предсказанная) оценка с прошлого n-1 шага на текущий

S_n – оценка полезного сигнала на текущем n-ном шаге.

V_n – дисперсия оценки полезного сигнала на текущем шаге

R – параметр модели авторегрессии первого порядка

σ_ξ² – параметр модели возбуждения

Все три параметра модели предполагаются известными. Считаем, что модель идентифицирована (обучена). Для того чтобы рекуррентный процесс начался, необходимо начальное условие.

S₀ – априорная оценка полезного сигнала

V₀ – априорная дисперсия

Эти две величины также предполагаются известными.

Алгоритм Калмана состоит из 4 уравнений. 3 уравнение называется уравнением фильтрации, оно формирует оценку сигнала, только оно должно реализовываться в реальном времени. 1 2 и 4 уравнения носят вспомогательный характер и могут быть реализованы заранее.

Последовательность K_n – значения коэффициента усиления фильтра Калмана может быть вычислена заранее и записана в память. В реальном времени мы извлекаем значения K_n из памяти и используем для вычисления оценки S_n.

Схема:



Физический смысл работы фильтра Калмана состоит в следующем:

Фильтр реализует идею прогноза и коррекции. На основе имеющейся модели полезного сигнала (в нашем случае модель авторегрессии) и на основе имеющейся прошлой оценки формируется прогноз (экстраполированная оценка) на следующий шаг. Затем происходит коррекция (вычисляется разность между прогнозом и вновь поступившим сигналом, эта разность называется невязка). Невязка умножается на весовой коэффициент, который учитывает все свойства модели процесса и наблюдения (в нем заложено знание о модели, о процессе, о помехах, которое у нас есть). Далее наш прогноз корректируется, далее процесс повторяется.

Фильтр Калмана очень прост в вычислительном отношении. На одном шаге фильтр Калмана требует только двух умножений и двух сложений. А все остальное считается заранее. Фильтр Калмана является оптимальным линейным фильтром. Среди всех линейных фильтров он обеспечивает минимальную дисперсию ошибки фильтрации (наилучшая точность). К недостаткам фильтра Калмана относится то, что он требует знания всех параметров модели.

В настоящее время до конца проблема разработки алгоритмов фильтрации продолжает решаться, в условиях сложных помеховых ситуаций.

Фильтр Калмана пригоден только для линейных задач, если задача не линейная.

Стратонович предложил теорию нелинейной фильтрации, фильтр Калмана оказался частной случаем. Фильтр Стратоновича колоссально сложен.

При проведении обучения моделей необходимо соблюдать алгоритмы обучения и алгоритмы фильтрации.

01 декабря

Вычислительная сложность алгоритма

Алгоритм

Абу́ Абдулла́х Муха́ммад ибн Муса́ аль-Хорезми́

Алгоритм – это последовательность действий (операций, шагов), которые нужно сделать чтобы получить решение задачи.

В задачах моделирования обычно используется численный алгоритм. Численный алгоритм – это последовательность арифметических операций, которые нужно выполнить чтобы получить решение задачи.

Желательные свойства алгоритма:

1. 
   Эффективность – выполнение алгоритма (получение решения задачи) при любых допустимых исходных данных за заданное время.
   
2. 
   Определенность – возможность точного формального описания всех шагов (операций), а также последовательности их выполнения
   
3. 
   Конечность – выполнение алгоритма при конкретных исходных данных за конечное число шагов.
   

Понятие вычислительной сложности

Наиболее распространенными критериями эффективности алгоритма являются: время выполнения алгоритма и размер памяти, необходимой для реализации алгоритма. Время зависит от числа арифметических операций, а также от производительности процессора. Будем считать оценку сложности алгоритма – число арифметических операций, необходимое для его реализации. Такая оценка называется временная сложность алгоритма. Есть еще понятие ёмкостной сложности – это объем требуемой памяти, для реализации алгоритма. Иногда возможен обмен между емкостной сложностью и временной сложностью. Далее будем рассматривать временную сложность алгоритма.

Функция сложности алгоритма

F(X₁…X_n, N) – функция сложности – зависимость числа арифметических операций в алгоритме от самих входных данных и от размера входных данных(числа входных данных).

Для численных алгоритмов также бывает ситуация, когда для одного набора входных данных сложность небольшая, а для другого набора сложность большая, а поскольку входные данные носят случайный характер, то вычислительная сложность оказывается случайной.

Функция сложности является возрастающей функцией, это значит, что с увеличением N, число операций растет. В общем случае, из-за случайного характера входных данных, функция сложности является случайной функцией.



Есть много численных алгоритмов, где функция сложность зависит только от объема входных данных, и не зависит от самих входных данных. В этом случае будет иметь вид возрастающей функции.



Для практической реализации алгоритмов, возникающих при моделировании, необходимо знать с какой скоростью растет функция сложности.

Асимптотическая сложность – F(N) <= Const * N

Алгоритмы по степени (скорости) роста функции сложность делятся на классы:

1. 
   Алгоритмы полиномиальной сложности – f(N) = O(N^m)
   
2. 
   Алгоритмы экспоненциальной сложности – f(N) = O(a^N)
   

Обратимся к алгоритмам полиномиальной сложности. Число m называется порядком сложности алгоритма (m может быть дробное). Если порядок сложности равен 1, то функция сложности это линейная функция. Говорят что это алгоритм с линейной сложностью (сложность первого порядка).

Когда m = 2, это алгоритмы с квадратичной сложностью (сложность второго порядка).

M = 3, алгоритм кубической сложности (третьего порядка).

При увеличении производительности вычислительного устройства в 1000 раз, размер входных данных алгоритма 1-ого порядка может быть увеличен тоже в 100 раз, для алгоритмов второго порядка может быть увеличен только в 31 раз, а для алгоритма 3-его порядка только в 10 раз.

Если требуется реализовывать алгоритмы полиномиальные высокого порядка сложности (3 и выше) или тем более алгоритмы экспоненциальной сложности, то требования к производительности процессора катастрофически вырастают.

Теория сложности решает две основные задачи:

1. 
   Анализ вычислительной сложности (подсчет числа операций в алгоритме)
   
2. 
   Уменьшений вычислительной сложности – задача упрощений алгоритма
   

Алгоритмы экспоненциальной сложности асимптотически всегда сложнее чем алгоритмы полиномиальной сложность (любого порядка), потому что экспонента растёт всегда быстрее чем полином в любой степени.



Скорее всего эти классы не эквивалентны, и поэтому в общем случае нельзя упростить алгоритм с экспоненциальной сложностью, до алгоритма с полиномиальной сложностью.

Подсчет вычислительной сложности алгоритма

Самый простой метод подсчета — это непосредственное вычисление числа операций. В случае если алгоритм носит сложный витиеватый характер, то используются рекуррентные способы подсчета вычислительной мощности.