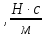Расчетно Графическое задание потермеху. ргр термех. На груз действует возмущающая сила, направление которой совпадает с осью
 Скачать 197.73 Kb. Скачать 197.73 Kb.
|
Условие:Груз массой  (материальная точка) прикреплен к пружине жесткости (материальная точка) прикреплен к пружине жесткости  . Начальная деформация пружины . Начальная деформация пружины  , начальная скорость груза , начальная скорость груза  . Массой пружины пренебречь. Начало координат взять в положении статического равновесия груза на пружине. Принять . Массой пружины пренебречь. Начало координат взять в положении статического равновесия груза на пружине. Принять  . . На груз действует возмущающая сила  , направление которой совпадает с осью , направление которой совпадает с осью 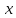 . . Для определения начальных условий в каждом варианте следует использовать условия крепления груза к концу  пружины: пружины:Варианты 11-15: К концу А недеформированной пружины прикрепляют груз, которому сообщают скорость, направленную вверх Задание:1) Составить закон свободных и вынужденных (на частоте возмущения  ) колебаний груза на пружине без сопротивления. Привести график процесса колебаний. ) колебаний груза на пружине без сопротивления. Привести график процесса колебаний.2) На груз дополнительно действует еще и сила сопротивления, пропорциональная первой степени скорости:  . .Определить значение резонансной амплитуды и построить, пользуясь формулой для амплитуды вынужденных колебаний, резонансную кривую в интервале изменения частоты возмущающей силы  , ,  – собственная частота свободных колебаний точки в конкретном варианте. Коэффициент сопротивления – собственная частота свободных колебаний точки в конкретном варианте. Коэффициент сопротивления  (или коэффициент динамичности (или коэффициент динамичности  ) амплитуда возмущающей силы ) амплитуда возмущающей силы  и ее частота и ее частота  даны в таблице 1. даны в таблице 1.Таблица 1 Исходные данные
Решение: 1) Найдем положение статического равновесия груза – точку  . Пусть . Пусть  – точка, соответствующая концу недеформированной пружины. Тогда – точка, соответствующая концу недеформированной пружины. Тогда  – статическая деформация, которой соответствует сила упругости – статическая деформация, которой соответствует сила упругости  . . Рассмотрим равновесие груза. На него действуют три силы:  , ,  и и  . Выберем ось . Выберем ось  и запишем уравнение равновесия в проекциях на эту ось: и запишем уравнение равновесия в проекциях на эту ось: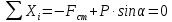 или или  , ,Откуда  Начало координат на оси 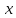 поместим в положение поместим в положение  статического равновесия груза. В этом положении статического равновесия груза. В этом положении 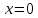 . .Определим частоту свободных колебаний груза 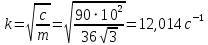 Дифференциальное уравнение вынужденных колебаний имеет вид: 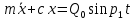  - амплитуда возмущающей силы. - амплитуда возмущающей силы.Его решение имеет вид:
 , ,  – произвольные постоянные интегрирования. – произвольные постоянные интегрирования.Здесь первые два слагаемыx представляют собой свободные колебания груза, третье слагаемое – вынужденные;  - амплитуда вынужденных колебаний. Таким образом, - амплитуда вынужденных колебаний. Таким образом,  Для определения постоянных  , ,  необходимо поставить начальные условия, т.е. определить смещение и скорость груза при необходимо поставить начальные условия, т.е. определить смещение и скорость груза при 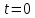 . В начальный момент груз находится в положении . В начальный момент груз находится в положении  , т.к. пружина была предварительно растянута на , т.к. пружина была предварительно растянута на  Тогда Тогда 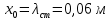  ч чТаким образом, имеем начальные условия:  м; м; 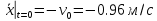 . Подставляя в эти начальные условия решение и его производную по времени . Подставляя в эти начальные условия решение и его производную по времени  , получим уравнения для определения постоянных С1 и С2 , получим уравнения для определения постоянных С1 и С2     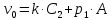  И закон колебаний приобретает вид:
График процесса приведен на рисунке:  2) Считая теперь, что на груз действует также сила сопротивления пропорциональная первой степени скорости, а частота возмущающей силы p является величиной переменной, построим резонансную кривую 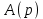 в интервале в интервале 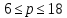 с-1. с-1.По формуле для резонансной амплитуды определим:     Задание. Нить с грузом на конце при своём движении из положения ОМ0 встречает в точке О1 тонкую проволочку, расположенную перпендикулярно плоскости чертежа, после чего груз начинает вращаться вокруг точки О1. Найти длину нити, если известно, что при  , натяжение нити равно нулю, и скорость груза β=0; ОО1= , натяжение нити равно нулю, и скорость груза β=0; ОО1= ОМ0= ОМ0= ; ;  . . Решение:  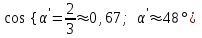 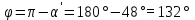 Скорость груза в точке М1 найдём с помощью теоремы об изменении кинетической энергии точки:  (1) (1)А – работа равнодействующей силы, по теореме о равнодействующей: А=АР+АN АР – работа силы тяжести; АN – работа реакции Реакция  в любом положении груза, поэтому АN=0 в любом положении груза, поэтому АN=0Работа силы тяжести А=Р∙Н1, где  Знак плюс поставлен потому, что конечное положение груза ниже начального. Тогда: 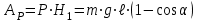 Подставим значение работы в уравнение (1):   (2) (2)Для нахождения скорости груза в точке М2, применим метод кинетостатики для точки. Приложим к грузу тангенциальную силу инерции  и центробежную силу и центробежную силу  и рассмотрим равновесие груза в точке М2: и рассмотрим равновесие груза в точке М2: 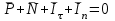 Спроектируем это векторное равенство на направление внешней нормали (n), тогда с учётом N=0,  , имеем , имеем 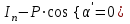 ; ;    (3) (3)Для нахождения длины нити снова воспользуемся теоремой об изменении кинетической энергии точки:  (4) (4)Знак минус поставлен потому, что конечное положение точки выше начального. 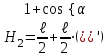 Подставим значение Н2,  из формулы (2) и из формулы (2) и  из формулы (3) в уравнение (4): из формулы (3) в уравнение (4):   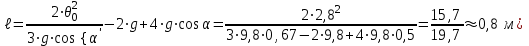 Значение  подставляем в формулу (3): подставляем в формулу (3): |