Практическая работа по исследований операций. Практическая_Егоровой.А.А_2ПИ. Найти множество Парето следующей двухкритериальной задачи
 Скачать 231.14 Kb.
|
|
Практическая работы Вариант 10 Выполнила: Студентка 24 группы ПИ Егорова Аделина А. Найти множество Парето следующей двухкритериальной задачи. F1(x)→min, F2(x)→min, при условии 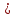 . Значения функций заданы таблицей
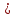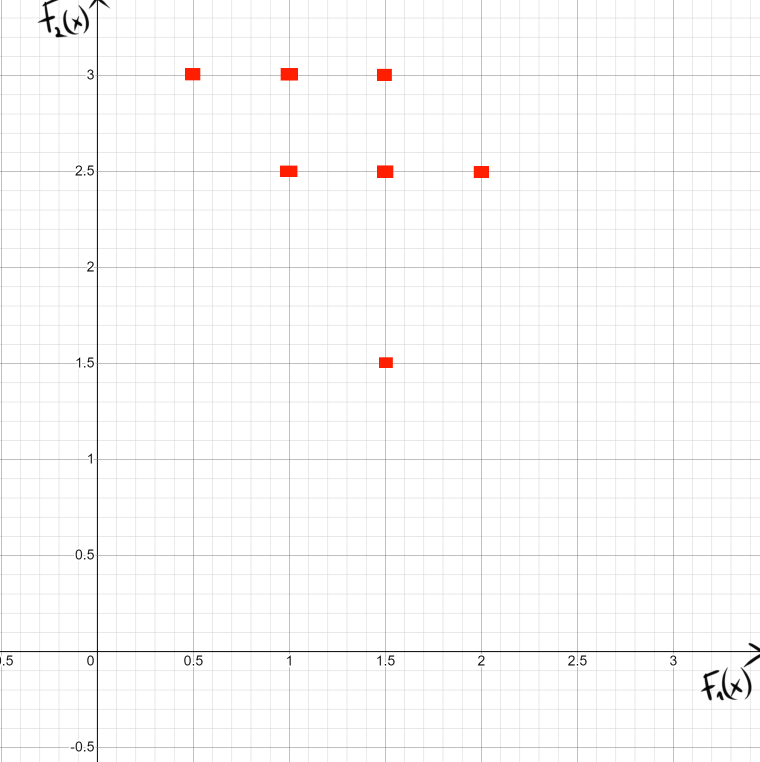Решение. Решим вопрос нахождения множества Парето данной задачи геометрически. Для этого изобразим на графике множество, состоящее из точек = (0,5;3),(1;3),(1,5;3),(1;2,5),(1,5;2,5),(2;2,5),(1,5;1,5)   С помощью графика найдем все точки с минимальным значением координаты 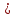. В данном случае это одна точка, имеющая координаты (0,5;3). Она войдет во множество оптимальных по Парето исходов. 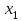Далее исключим из рассмотрения все точки, координаты  которых не превосходят, а координаты 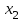 больше или равны координатам найденной точки (0,5;3) ( это (1;3) и (1,5;3) ). Снова из оставшихся точек выберем все с наименьшем значением 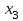 . Это точка с координатами (1;2,5). 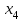Из оставшихся две точки (1,5;2,5) и (2;2,5) нам не подходят, поскольку их координаты  больше первой координаты выбранной точки (1;2,5), а координаты 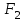 равны второй координате этой точки. Значит, соответствующие им стратегии являются доминируемыми. Что же касается точки (1,5;1,5), то она войдет во множество оптимальных по Парето точек. Окончательно получили, что множество Парето данной задачи состоит из трех точек - (0,5;3), (1;2,5), (1,5;1,5). Они отвечают стратегиям под номерами 1, 4 и 7 соответственно. Таким образом, 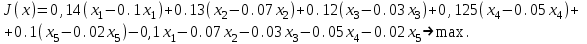 .Ответ: 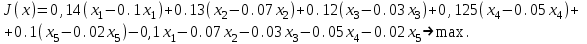.Геометрически решить задачу линейного программирования: 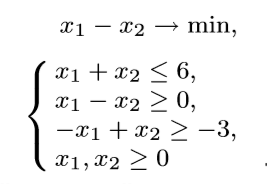 Решение. Строим область допустимых решений, т.е. геометрическое место точек, в котором одновременно удовлетворяются все ограничения данной ЗЛП. Каждое из неравенств системы ограничений нашей задачи геометрически в системе координат ( 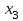, 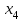) определяет полуплоскость соответственно с граничными прямыми.Первому ограничению соответствует прямая, пересекающая координатные оси в точках с координатами ( 0, 6 ) и ( 6, 0 ). Второму ограничению соответствует прямая, пересекающая координатные оси в точках с координатами ( 0, 0 ) и ( 1, 1 ). Третьему ограничению соответствует прямая, пересекающая координатные оси в точках с координатами ( 0, -3 ) и ( 3, 0 ). Четвёртому ограничению соответствует прямая, пересекающая координатные оси в точке с координатами ( 0, 0 ) и проходящая параллельно оси 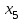 .Пятому ограничению соответствует прямая, пересекающая координатные оси в точке с координатами ( 0, 0 ) и проходящая параллельно оси 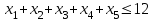 .Области, в которых выполняются соответствующие ограничения в виде неравенств, указаны на рисунке стрелками, направленными в сторону допустимых значений переменных. Полученная область допустимых решений выделена на рисунке серым цветом. 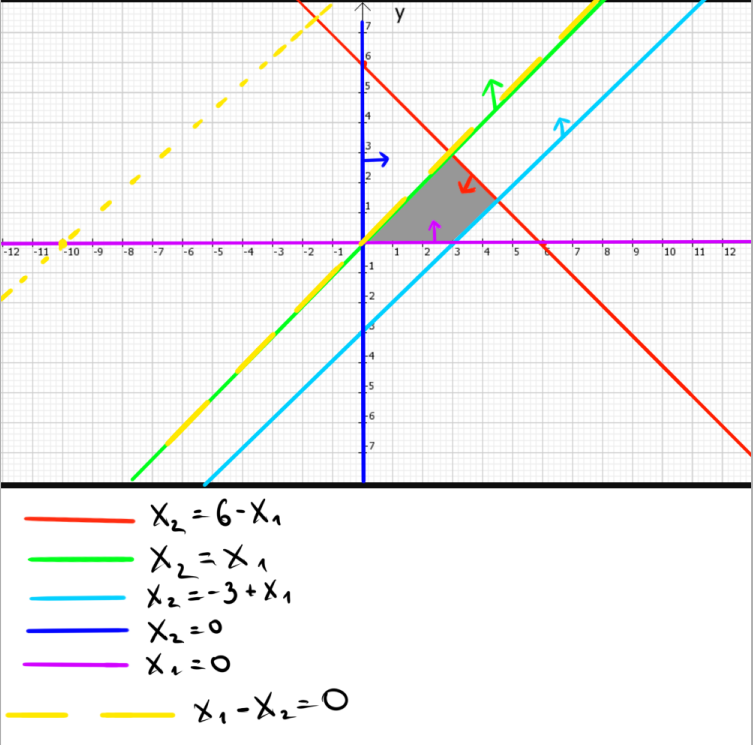 Прямая x1-x2=0 пересекает область в точке (0;0). Так как точка (0;0) получена в результате пересечения прямых x2=0 и x1=0, то ее координаты удовлетворяют уравнениям этих прямых: x2=0 x1=0 Решив систему уравнений, получим: x1=0, x2=0. Откуда найдем минимальное значение целевой функции: F(X) = 1*0 - 1*0 = 0 Ответ:0 4. Перейти к двойственной и решить задачу линейного программирования: 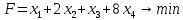 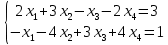 Решение. 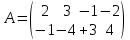 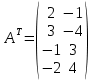 Двойственная задача имеет вид: 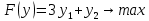 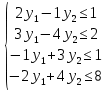 y1 , y2 – произвольные по знаку Решение базовым симплекс-методом Для каждого ограничения с неравенством добавляем дополнительные переменные y3..y6. Перепишем ограничения в каноническом виде: 2·y1 - y2 + y3 = 1 3·y1 - 4·y2 + y4 = 2 - y1 + 3·y2 + y5 = 1 - 2·y1 + 4·y2 + y6 = 8 Ищем начальное базисное решение: Ограничение 1 содержит неравенство, базисной будет добавленная дополнительная переменная y3 Ограничение 2 содержит неравенство, базисной будет добавленная дополнительная переменная y4 Ограничение 3 содержит неравенство, базисной будет добавленная дополнительная переменная y5 Ограничение 4 содержит неравенство, базисной будет добавленная дополнительная переменная y6 Начальная симплекс-таблица
Вычисляем дельты: Δi = C3·a1i + C4·a2i + C5·a3i + C6·a4i - Ci Симплекс-таблица с дельтами
|