Определение момента инерции маятника обербека
 Скачать 127.45 Kb. Скачать 127.45 Kb.
|
|
Лабораторнаяработа№12 ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАЯТНИКА ОБЕРБЕКАДата выполнения Время на подготовку и допуск к лабораторной работе: 30 минут. Время на выполнение экспериментов: 30 минут. Время на оформление отчета и расчёты: 30 минут. Цель работы.Ознакомится с понятием момента инерции вращающегося тела. Определить зависимость момента инерции маятника Обербека от положения грузов и массы подвеса. Оборудование.Маятник Обербека. Грузы разной массы. Секундомер. Линейка. Основные сведения.Любое твердое тело, имеющее ось вращения, будет совершать вращательное движение, если к нему приложить внешнюю силу Fвн., линия действия которой не проходит через ось вращения (Рис. 12.1). 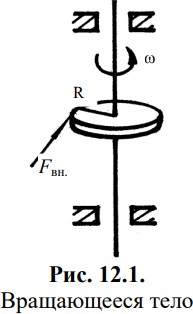 Перпендикуляр, опущенный из оси вращения на линию действия силы, называется плечом силы R. Произведение силы Fвн. на плечо R называется моментом силы. M = Fвн. · R. Итак, чтобы тело вращалось, необходимо приложить момент силы. Если на тело действует постоянный момент силы, то тело будет вращаться равноускоренно с постоянным угловым ускорением 𝜀. где J — момент инерции вращающегося тела. Формула (12.1) выражает второй закон Ньютона для вращательного движения. Момент инерции выполняет роль массы тела, а момент силы — роль силы. Моментом инерции материальной точки принято называть произведение массы точки на квадрат ее расстояния до оси вращения. J=mr2. Если тело разбить на n элементов, то момент инерции всего тела будет вычисляться следующим образом где i — номер элемента тела. В данной лабораторной работе определяется момент инерции маятника Обербека (Рис. 12.2). Маятник состоит из четырех стальных стержней, расположенных под прямым углом и вставленных во втулку. На стержнях укреплены грузики одинаковой массы m0. Эти грузики можно перемещать вдоль стальных стержней. Изменяя их расстояние от оси вращения, можно изменить момент инерции маятника. На ось вращения насажен шкив, радиусом R. На шкив намотан шнур, свободный конец которого имеет специальную подставку для закрепления на ней различных грузов. Груз массой m, опускаясь на шнуре, приводит во вращение шкив и стержни с грузиками массой m0. 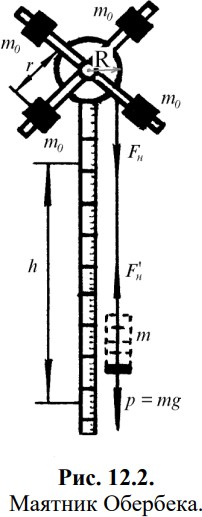 Найдем величину момента силы M, вращающего маятник, и его угловое ускорение 𝜀. Момент силы M определим по формуле M = FнR, где Fн — сила, вызывающая вращение маятника (сила натяжения шнура), R — радиус шкива (плечо силы). Если сила тяжести груза P = mg больше силы натяжения Fн, то груз будет опускаться с ускорением под действием силы Fуск. = ma. P – Fн = Fуск. Откуда Fн = mg – ma = m(g – a). Ускорение силы тяжести g (ускорение свободного падения) значительно больше линейного ускорения a , с которым груз движется вниз. Поэтому можно считать приближенно Величину углового ускорения 𝜀 можно найти из следующих соображений. Шнур, разматываясь со шкива, не скользит по нему и, следовательно, каждая точка шкива в месте соприкосновения со шнуром будет двигаться с тем же линейным ускорением, что и сам спускающийся груз. Между угловым ускорением точки на окружности и ее линейным ускорением существует зависимость. Величину линейного ускорения спускающегося груза можно определить по формуле равноускоренного поступательного движения. Если t – время, в течение которого груз проходит путь h с ускорением a, то Таким образом, угловое ускорение Подставляя в формулу (12.1) значения момента силы M из формулы (12.2) и угловое ускорение из формулы (12.4), получим расчетную формулу для момента инерции маятника Обербека. Все величины, стоящие в правой части формулы (12.5). m — масса груза, R радиус шкива, t — время падения груза и h — высота падения груза, измеряются на опыте. Формула (12.5) получена в предположении, что a << g. В том, что линейное ускорение груза a действительно мало по сравнению с ускорением свободного падения g, нетрудно убедиться на основании опытных данных. Подставляя полученные экспериментальные значения h и t в формулу (12.3), можно убедиться, что a << g. Порядок выполнения работыОпределите зависимость момента инерции маятника Обербека от расстояния r грузиков m0 на стержнях крестовины от оси вращения. расположите грузики m0 на стержнях крестовины на расстоянии r1 от оси вращения; намотайте на шкив шнур, свободный конец которого имеет специальную подставку для грузов; придерживая крестовину, положите на подставку груз m; отметьте деление на линейке, соответствующее основанию подставки с грузом m; отпустите груз для свободного падения и одновременно включите секундомер, но не толкайте крестовину; выключите секундомер, как только подставка с грузом достигнет нижней отметки на линейке; определите по секундомеру время падения груза t1; результат измерения t1 запишите в Таб. 12.1; повторите опыт еще 2 раза, т. е. измерьте время t2 и t3 и из 3-х значений взять среднее tср.; расположите грузики m0 на стержнях крестовины на расстоянии r2 от оси вращения; определите по той же методике среднее время падения tср. груза m; измерьте по линейке высоту падения h груза m. Проделайте те же измерения tср. для расстояний r3, r4, r5. Результаты измерений занесите в Таб. 12.1. Таб. 12.1.
R= 4 см Исследуйте зависимость момента инерции маятника Обербека от массы подвеса m, висящего на нити. Для этого: установите грузики m0 на стержнях крестовины на расстоянии r5; намотайте на шкив шнур; придерживая крестовину, положите на подставку груз m1; отметьте деление шкалы, соответствующее основанию подставки; опустите груз для свободного падения, одновременно включите секундомер; выключите секундомер, как только подставка с грузом m1 достигнет нижней отметки на линейке; определите по секундомеру время падения груза t1; результаты измерения запишите в Таб. 12.2. повторите опыт еще два раза и из 3-х значений вычислите значение tср.; Проделайте опыты с грузами m2, m3, m4, m5. Результаты измерений занесите в Таб. 12.2. Таб. 12.2.
R= 4 см Обработка результатов измерения По результатам Таб. 12.1 рассчитайте по формуле  моменты инерции маятника Обербека для пяти положений грузиков на стержнях крестовины. Результаты расчетов занесите в Таб. 12.1. Постройте графики зависимости J = f(r) и J = f (r2) (см. п. 3 Правил оформления…) при постоянной массе m.  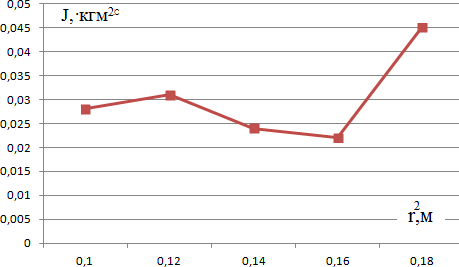 По результатам Таб. 12.2 рассчитайте моменты инерции маятника Обербека при постоянном r1 и различных массах груза m1, m2, m3, m4, m5. Результаты расчета занесите в Таб. 12.2. Постройте график зависимости J = f(m) при r1 = const. 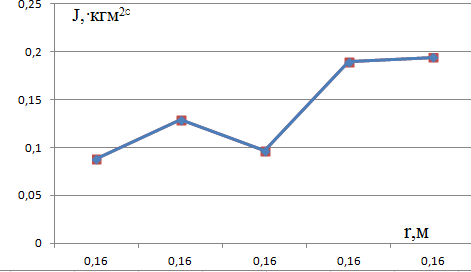 Сделайте выводы. Вывод: момент инерции маятника зависит от массы грузов и расстояния грузов от оси вращения прямопропорционально. По данным расчета момента инерции таблицы 12.2 произведите обработку результатов измерения, вычислите среднее значение момента инерции маятника Jcp и абсолютную погрешность измерения ∆J. Окончательный =обработке результатов измерений»). 𝐽ср = 0,139 кг ∙ м2  ∑5 (𝐽𝑖 − 𝐽𝑐р)2 ∆𝐽 = 2√𝑖=1 𝑛(𝑛 − 1) ∆𝐽 = 0,044 кг ∙ м2 Тогда 𝐽 = (0,139 ± 0,044) кг ∙ м2 Определите относительную погрешность измерения по формуле 𝛿=0,022 ∙ 100% = 15,8% 0,139 Контрольные вопросы Дайте определение момента инерции. Каков физический смысл момента инерции? Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Момент инерции является мерой инертности тела при вращении (физический смысл) Почему с увеличением расстояния r грузиков m0 от оси вращения момент инерции возрастает. Какая это зависимость? Возрастает так как момент инерции зависит от распределения массы в пространстве. Зависимость является прямой пропорциональностью Поясните вид графика зависимости J = f(m) при r = const. Зависимость момента инерции тела от массы является прямой пропорциональностью От чего зависит момент инерции твердого тела? От массы тела, от квадрата расстояния от оси вращения Сформулируйте основной закон динамики вращательного движения. Основной закон динамики вращения (II закон Ньютона для вращательного движения): Момент вращающей силы, приложенной к телу, равен произведению момента инерции тела на угловое ускорение. Замечания преподавателя Оценка за работу:баллов. Подпись преподавателя: |
