Экзамен Физика 1 сем ЛЭТИ. Экз44_Физика. Основы механики
 Скачать 4.84 Mb.
|
|
Физика Основы механики Состояние механической системы Законы Ньютона. Уравнения движения и начальные условия. Движение тела, брошенного под углом к горизонту. Максимальная высота подъема и дальность полета тела. С  остоянием механической системы называется набор одновременных значений радиусов-векторов и скоростей всех ее точек.   Состояние механической системы. Законы Ньютона. Уравнения движения и начальные условия Движение тела в диссипативной среде. Время и путь релаксации. Мгновенная мощность рассеяния. Механическое равновесие — состояние механической системы, при котором сумма векторов всех сил, действующих на каждую её частицу, равна нулю и сумма моментов всех сил, приложенных к телу относительно любой произвольно взятой оси вращения, также равна нулю. Диссипативная система характеризуется спонтанным появлением сложной, зачастую хаотичной структуры. Отличительная особенность таких систем — несохранение объёма в фазовом пространстве Время релаксации — период времени, за который амплитудное значение возмущения в выведенной из равновесия физической системе уменьшается в e раз. Мгновенная мощность - предел, к которому стремится средняя мощность за бесконечно малый промежуток времени. Гармонические колебания. Уравнение движения. Амплитуда, частота и фаза колебаний, связь с начальными условиями Скорость и ускорение при гармонических колебаниях. Амплитуда – величина наибольшего отклонения системы от положения равновесия. Постоянная положительная величина. Её значение определяется величиной первоначального отклонения или толчка, которым система была выведена из состояния равновесия. Гармонические колебания - колебания, при которых физическая величина изменяется с течением времени по закону синуса или косинуса. Частота колебаний – число колебаний в единицу времени. Частота связана с продолжительностью одного колебания  соотношением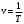 .Фаза – величина стоящая под знаком косинуса  . Постоянная  представляет собой значение фазы в момент времени 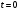 и называется начальной фазой колебания. С изменением начала отсчёта времени будет изменяться и . (стр. 227)Скорость  .Ускорение  .Упругие силы. Колебания пружинного маятника. Сила и энергия при гармонических колебаниях. Сохранение энергии. Фазовая траектория и потенциальная кривая гармонического осциллятора. Сила упругости  . Может случиться, что сила иного происхождения обнаруживает такую же закономерность т.е. оказывается равной 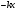 , где  - постоянная положительная величина. Силы такого вида принято называть квазиупругими.Траектория (стр. 231). Сила  Энергия  Затухающие колебания пружинного маятника Апериодический и колебательный процесс. Критическое затухание. Время релаксации, декремент затухания и добротность. Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Добротность – характеристика колебательной системы  Декремент затухания – отношение значения амплитуд, соответствующих моментам времени, отличающимся на период.  Время релаксации — период времени, за который амплитудное значение возмущения в выведенной из равновесия физической системе уменьшается в e раз. Система материальных точек. Степени свободы. Центр масс (центр инерции) Движение системы материальных точек. Сохранение импульса. Система материальных точек: Тела, входящие в систему, могут взаимодействовать как между собой, так и с телами, не принадлежащими данной системе. Силы, действующие на систему, внутренние и внешние. Если внешние силы отсутствуют, то система замкнутая. Материальная точка – тело, размерами которого в условиях данной задачи можно пренебречь. Степени свободы — характеристики движения механической системы. Число степеней свободы определяет минимальное количество независимых переменных, необходимых для полного описания состояния механической системы. Центр инерции системы – точка, положение которой в пространстве задаётся радиусом-вектором 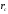 , который характеризует движение этой системы. Центр инерции совпадает с центром тяжести системы (в однородном поле сил тяжести). Задаётся следующим выражением:  .Сохранение импульса – импульс замкнутой системы материальных точек остаётся постоянным. Сохранение импульса. Упругий нецентральный улар двух шаров. Абсолютно упругий удар – удар, при котором механическая энергия тел не переходит в другие, немеханические, виды энергии. При таком ударе кинетическая энергия переходит полностью или частично в потенциальную энергию упругой деформации. (стр. 103-104) П 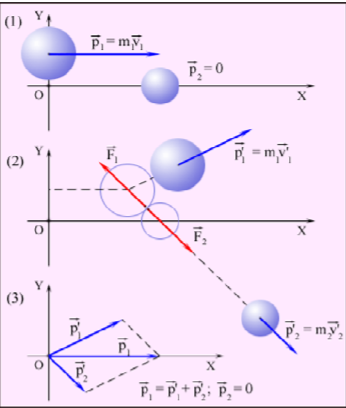 ри нецентральном упругом соударении скорости частиц (шаров) до и после столкновения не направлены по одной прямой. Частным случаем нецентрального упругого удара может служить соударения двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров. После нецентрального соударения шары разлетаются под некоторым углом друг к другу. Для определения скоростей после удара нужно знать положение линии центров в момент удара или расстояние между двумя линиями, проведенными через центры шаров параллельно вектору скорости налетающего шара. Если массы шаров одинаковы, то векторы скоростей и шаров после упругого соударения всегда направлены перпендикулярно друг к другу.Система материальных точек. Степени свободы. Центр масс (центр инерции). Движение системы материальных точек Поступательное движение и вращение Сохранение момента импульса. (стр. 127) (стр.134) В 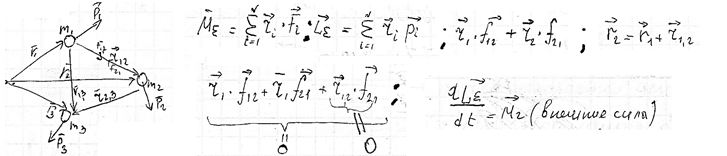 опрос 6 Закон сохранения момента импульса - векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной в случае равновесия системы. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем. Если при движении твердого тела можно найти точку, для которой радиус векторы проведенные из этой точки в произвольную точку тела, описывают окружности (с общим центром), то такое движение называется вращением, а точка называется центром вращения. Если через центр вращения можно провести прямую, то в проекции всех радиус векторов, проведенных из центра вращения, на направление перпендикулярное данной прямой, так же описывает окружности, центры которых на прямой, то такая прямая называется осью вращения. Работа силы и кинетическая энергия. Силовое поле. Работа сил поля и потенциальная энергия. Консервативные силы и потенциальные поля. Связь силы и потенциальной энергии. Сохранение энергии. (стр. 86-89) Силовое поле - часть пространства (ограниченная или неограниченная), в каждой точке которой на помещенную туда материальную частицу действует определённая по величине и направлению сила, зависящая или только от координат x, у, z этой точки, или же от координат x, у, г и времени t. В первом случае С. п. называется стационарным, а во втором — нестационарным. Если сила во всех точках С. п. имеет одно и то же значение, т. е. не зависит ни от координат, ни от времени, то С. п. называется однородным. Вращательное движение. Угловая скорость и угловое ускорение. Момент силы и момент импульса. Момент инерции. Основное уравнение динамики вращательного движения. При вращательном движении все точки твёрдого тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Для описания вращательного движения нужно задать положение в пространстве оси вращения и угловую скорость тела в каждый момент времени. Угловая скорость  , где ∆t – время, за которое совершается поворот ∆φ.Угловое ускорение  .(стр.127) Момент силы вращения – произведение силы умноженную на радиус (длина плеча) Момент импульса относительно точки O  ,  .Момент инерции - величина, характеризующая распределение масс в теле. 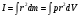 .Основное уравнение динамики вращательного движения (относительно z)  , где   Момент инерции твердого тела. Теорема Штейнера. Основное уравнение вращательного движения. Ускорение центра масс полого цилиндра, скатывающегося с наклонной плоскости. Теорема Штейнера – момент инерции относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр инерции тела, и произведения массы тела на квадрат расстояния между осями.  . Момент инерции твердого тела. Теорема Штейнера. Основное уравнение динамики вращательного движения. Ускорение центра масс сплошного цилиндра, скатывающегося с наклонной плоскости.  Момент инерции твердого тела, Теорема Штейнера. Основное уравнение динамики вращательного движения. Ускорение центра масс шара, скатывающегося с наклонной плоскости.  Физический маятник. Уравнение движения физического маятника. Приведенная длина физического маятника. Период колебаний и приведенная длина однородного стержня, качающегося в поле силы тяжести. Физический маятник – твердое тело, способное совершать колебания вокруг неподвижной точки, не совпадающей с его центром инерции. Основное уравнение  , где M(f) – момент сил, вызванный силами трения среды.   . Физический маятник. Уравнение движения физического маятника Приведенная длина физического маятника. Период колебаний и приведенная длина тонкого кольца, качающегося в полe силы тяжести.  Физический маятник. Уравнение движения физического маятника. Приведенная длина физического маятника. Период колебании и приведенная длина сплошного диска, качающегося в поле силы тяжести.  Физический маятник. Уравнение движения физического маятника. Приведенная длина физического маятника. Период колебаний и приведенная длина однородного шара качающегося в поле силы тяжести.  Волновые процессы. Продольные и поперечные волны. Уравнение плоской волны. Период и частота колебаний волнового процесса. Длина волны и волновое число. Волновое уравнение. Фазовая скорость. Волна – процесс распространения колебаний в пространстве. Волны бывают продольные и поперечные. В продольных волнах частицы среды колеблются вдоль линии, совпадающей с направлением распространения колебаний. В поперечных волнах частицы среды колеблются перпендикулярно направлению распространения волны. Уравнение плоской волны  .Фазовая скорость – скорость перемещения фазы.  Период и частота  , 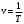Длина волны 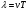 .Волновое число 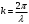 .Волновое уравнение  Волновые процессы. Волновое уравнение. Продольные и поперечные волны. Уравнение плоской волны. Перенос энергии в волновом процессе. Объемная плотность энергии. Вектор Умова. Среда, в которой возникает волна, обладает дополнительным запасом энергии. Эта энергия доставляется от источника колебаний в различные точки среды самой волной, следовательно, волна переносит с собой энергию. О  бъёмная плотность энергии Вектор Умова – вектор плотности потока  Основы молекулярной-кинетической теории и термодинамики Динамический, термодинамический и статистический методы описании макросистем. Параметры и функции состояния. Микро- и макросостояния. Вероятность состояния. Термодинамическая вероятность. Энтропия в статистической физике. Параметры состояния – всякая система может находиться в различных состояниях, отличающихся температурой, давлением, объёмом и т.п. (величины, характеризующие состояние системы) Динамический метод не применяется. Движения микрочастиц описывается законами квантовой механики. Их положение в принципе не может быть предсказано, положение частицы в некоторой области является случайным событием.  Функция состояния в термодинамике - функция независимых параметров, определяющих равновесное состояние термодинамической системы.  Первое начало термодинамики. Уравнение состояния идеального газа. Работа и внутренняя энергия. Теплоемкость. Изотермический процесс (стр. 310) Первое начало термодинамики – количество тепла, сообщённое системе, идёт на приращение внутренней энергии системы и на совершение системой работы над внешними телами. Уравнение состояния идеального газа 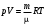 .Внутренняя энергия системы тел равна сумме внутренней энергии каждого из тел в отдельности и энергии взаимодействия между телами, представляющей собой энергию межмолекулярного воздействия в тонком слое на границе между телами.  Теплоёмкость – величина, равная количеству тепла, которое нужно сообщить телу, чтобы повысить его температуру на один градус. Изотермический процесс – переход газа из одного состояния в другое, совершающийся при постоянной температуре Первое начало термодинамики. Уравнение состояния идеального газа. Работа и внутренняя энергия. Теплоемкость. Изохорный процесс. Изохорный процесс – процесс совершающийся при постоянном объёме. Первое начало термодинамики. Уравнение состояния идеального газа. Работа и внутренняя энергия. Теплоемкость. Изобарный процесс. Изобарный процесс – процесс происходящий при постоянном давлении Первое начало термодинамики. Уравнение состояния идеального газа. Работа и внутренняя энергия. Изобарная и изохорная теплоемкости. Уравнение Майера.  Уравнение Майера 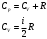 .Первое начало термодинамики. Уравнение состояния идеального газа. Работа и внутренняя энергия. Теплоемкость. Адиабатный процесс. Уравнение Пуассона. Уравнение Пуассона  Адиабатный процесс – процесс, протекающий без теплообмена с внешней средой. Показатель адиабаты  .Политропный процесс. Уравнение политропы. Показатель политропы. Работа в политропном процессе. Показатель политропы и теплоемкость процесса. Процессы с отрицательной теплоемкостью. Политропный процесс – давление и объём идеального газа связаны соотношением 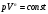 Показатель политропы -  .При 1 Внутренняя энергия идеального газа. Равномерное распределение энергии по степеням свободы газовой молекулы. Постулат Максвелла. Средняя энергия хаотического движения молекулы. Постоянная Больцмана и универсальная газовая постоянная. Молярные теплоемкости идеального газа. Равновесные и неравновесные процессы. Обратимость процесса. Циклы. Тепловая машина. Цикл Карно. Обратимость тепловой машины. Коэффициент полезного действия и холодильный коэффициент. Цикл Карно. Коэффициент полезного действия идеальной тепловой машины. «Обесценивание теплоты нагревателя». Идеальная тепловая машина и проблемы экологии. Цикл Карно - это идеальный обратимый круговой процесс, состоящий из двух адиабатных и двух изотермических процессов. КПД  .При этом с ростом энтропии происходит «обесценивание» энергии. Потеря ею способности к дальнейшим самопроизвольным превращениям в другие виды энергии.  Обратимые и необратимые процессы. Приведенная теплота. Направленность процесса теплопередачи. Приведенная теплота в термодинамических циклах. Неравенство Клаузиуса. Энтропия. Второе начало термодинамики.  Приведённое количество тепла – отношение количества тепла, полученного системой от какого-либо тела, к температуре этого тела. Неравенство Клаузиуса  .Второе начало термодинамики – невозможны такие процессы, единственным конечным результатом которых был бы переход тепла от тела, менее нагретого, к телу, более нагретому. Энтропия и приведенная теплота. Второе начало термодинамики и направление процесса. Закон возрастания энтропии. Идеальная тепловая машина и возрастание энтропии.  Закон возрастания энтропии – в любом процессе, который осуществляется в адиабатически изолированной системе, энтропия либо возрастает, либо остаётся постоянной. Приведенная теплота и энтропия. Расчет изменения энтропии в различных процессах. Энтропия и термодинамическая вероятность. Формула Больцмана. Вероятностный смысл второго начала термодинамики. Основными процессами в термодинамике являются: · изохорный, протекающий при постоянном объеме; · изобарный, протекающий при постоянном давлении; · изотермический, происходящий при постоянной температуре; · адиабатный, при котором теплообмен с окружающей средой отсутствует. Изохорный процесс При изохорном процессе выполняется условие V = const. Из уравнения состояния идеального газа (pV = RT) следует: p / T = R / V = const, т. е. давление газа прямо пропорционально его абсолютной температуре: p2 / p1 = T2 / T1. Изменение энтропии в изохорном процессе определяется по формуле: s2 – s1 = Δs = cv ln (p2 / p1) = cv ln (T2 / T1) Изобарный процесс Изобарным называется процесс, протекающий при постоянном давлении p = const. Из уравнения состояния идеального газа следует: V / T = R / p = const. Изменение энтропии будет равно: s2 – s1= Δs = cp ln (T2 / T1). Изотермический процесс При изотермическом процессе температура рабочего тела остается постоянной T = const, следовательно: pV = RT = const Изменение энтропии равно: s2 – s1 = Δs = Rln(p1/p2) = R ln(V2 / V1). Адиабатный процесс Адиабатным называется процесс изменения состояния газа, который происходит без теплообмена с окружающей средой (Q = 0). Уравнение кривой адиабатного процесса (адиабаты) в p-V диаграмме имеет вид: pV k = const. В этом выражении k носит название показателя адиабаты (так же ее называют коэффициентом Пуассона). Изменение энтропии равно: ΔS = S2 – S1 = 0, т.е. S2= S1. Формула Больцмана  Законы равновесного распределения. Статистика Больцмана Распределение молекул по скоростям. Средние тепловые скорости молекул идеального газа. Закон распределения Больцмана -  .  Средняя тепловая квадратичная скорость  .Законы равновесного распределения. Статистика Больцмана. Распределение молекул в потенциальном поле. Барометрическая формула. Барометрическая формула  . Давление убывает с высотой тем быстрее, чем тяжелее газ и чем ниже температура.Распределение в поле и есть закон распределения Больцмана. Явления переноса. Обобщенное уравнение переноса. Коэффициент переноса. Поток качества. Явления переноса – внутреннее трение (вязкость), теплопроводность, диффузия. Обобщённое уравнение переноса   Явления переноса. Диффузия. Уравнение Фика. Коэффициент диффузии. Поток частиц и перенос массы. Диффузия – явление самопроизвольного взаимного проникновения соприкасающихся веществ друг в друга вследствие теплового движения атомов или молекул вещества, приводящее к выравниванию их концентраций по всему занимаемому объёму.  Явления переноса. Вязкость (внутреннее трение). Уравнение Ньютона. Коэффициент вязкости. Градиент скорости и перенос импульса. Вязкость – свойство текучих сред оказывать сопротивление перемещению частей среды относительно друг друга.   Явления переноса. Теплопроводность. Уравнение Фурье. Коэффициент теплопроводности. Поток энергии и градиент температуры. Теплопроводность – процесс передачи теплоты от более нагретых участков тела менее нагретым в результате теплового движения молекул    Реальные газы. Поправки на объем молекул и внутреннее давление. Уравнение Ван-дер-Ваальса. Изотермы Ван-дер-Ваальса и изотермы реального газа. Критическая изотерма. Сжижение газа. Внутренняя энергия реального газа. Р   еальный газ – газ, свойства которого зависят от взаимодействия молекул.     |