Моделирование 2 (5). Отчет по лабораторной работе по дисциплине моделирование транспортных процессов
 Скачать 123.11 Kb. Скачать 123.11 Kb.
|
 ФЕДЕРАЛЬНОЕ АГЕНТСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА Федеральное государственное бюджетное образовательное учреждение высшего образования «Государственный университет морского и речного флота имени адмирала С.О. Макарова» __________________________________________________________________ КАФЕДРА МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ И ПРИКЛАДНОЙ ИНФОРМАТИКИ ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ № 2. ПО ДИСЦИПЛИНЕ «МОДЕЛИРОВАНИЕ ТРАНСПОРТНЫХ ПРОЦЕССОВ» Математическое описание грузовой обработки судна Выполнил: ст.гр.УВТ-32 Никонова С.А Проверил: доцент Шилкин В.П Санкт-Петербург 2020 Задачи Задача: методами математической статистики необходимо установить аналитические выражения для формализации случайного процесса продолжительности грузовой обработки судов в порту. Последовательность выполнения работы Определить среднюю продолжительность грузовой обработки и её среднее квадратическое отклонение; С помощью принятого критерия согласия (критерия Пирсона) проверить возможность замены эмпирического распределения времени грузовой обработки: - показательным законом распределения; - нормальным законом распределения. Построить график функции распределения продолжительности грузовой обработки эмпирического и теоретических распределений. По закону, с которым согласуется распределение фактических данных, определить вероятность того, что судно будет обработано не более чем: - за среднее время обслуживания; - за минимальное время обслуживания; - за максимальное время обслуживания. Для выполнения задания на основании исходных данных строится вспомогательная таблица для показательного закона распределения (таблица 2) 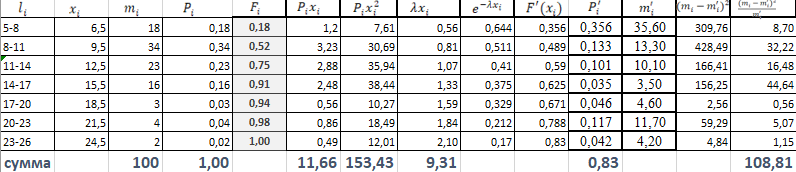 где Число интервалов (n) определяется по формуле Старжесса: n = 1 + 3,322lgN, где N – общее число наблюдений (N=100). n = 1 + 3,322 ∙ lg100 =7,644 Величина интервала (его ширина) определяется по формуле: 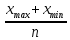 , ,где 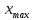 -значение максимального элемента в совокупности, -значение максимального элемента в совокупности,xmin – значение минимального элемента в совокупности. 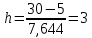 Для непрерывных случайных величин (как, например, время) в таблице верхняя граница предыдущего интервала равна нижней границе последующего интервала, но это не означает, что данное число входит в оба интервала. Принимается соглашение о том, какая граница принадлежит интервалу – верхняя или нижняя, и в дальнейшем оно соблюдается.(верхняя) λ – параметр показательного закона, равный величине, обратной математическому ожиданию (средней) продолжительности обработки судов:  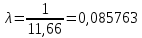 При расчете таблицы легко определить среднее значение (математическое ожидание): 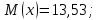 дисперсию:  ; ;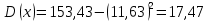 среднее квадратическое отклонение: 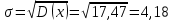 . .χ2 – критерий Пирсона: 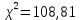 В этом случае расхождения между эмпирическими и теоретическими частотами нельзя считать случайными и несущественными. Гипотеза о соответствии эмпирического распределения показательному отвергается. Эмпирическое распределение нельзя заменить теоретическим. Для проверки возможности замены эмпирического распределения продолжительности обработки судов нормальным законом распределения заполняется вспомогательная таблица 2. Таблица 2 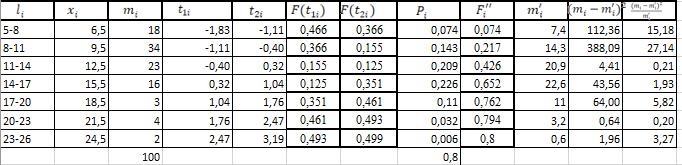 где 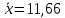 ; ;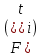 - функция Лапласа, значения которой определяются по таблице 2 справочных материалов; - функция Лапласа, значения которой определяются по таблице 2 справочных материалов;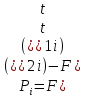 ; ;По полученному значению критерия Пирсона χ2 делается вывод о невозможности замены эмпирического распределения продолжительности обработки судов нормальным законом распределения. 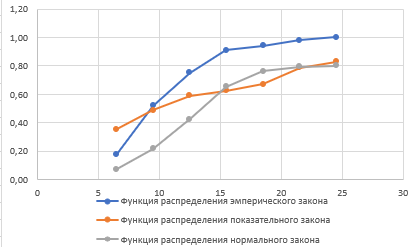 Рисунок 1. График функции распределения Распределение фактических данных не согласуется ни с показательным распределением, ни с нормальным распределением. Поэтому приведенные ниже выводы делаются по эмпирической вероятности Вероятность того, что судно будет обработано не более чем: - за среднее время обслуживания: Р(х - за минимальное время обслуживания: Р(х - за максимальное время обслуживания: P= 100%. |
