Лабораторная работа Зоны Френеля. Мамедов Зоны френеля. Отчет по лабораторной работе по дисциплине Электродинамика и распространение радиоволн
 Скачать 162.05 Kb. Скачать 162.05 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра сверхвысокочастотной и квантовой радиотехники (СВЧ и КР) ИССЛЕДОВАНИЕ ЗОН ФРЕНЕЛЯ И ДИФРАКЦИИ РАДИОВОЛН Отчет по лабораторной работе по дисциплине «Электродинамика и распространение радиоволн» Выполнил: студенты гр. 140-1 _____ А.В Мамедов Проверил: доцент каф.СВЧиКР ____А.С. Запасной «_» апреля 2022г Томск 2022 1 Введение Целью данной лабораторной работы является: 1) Знакомство с понятием зон Френеля в теории дифракции. 2) экспериментальное определение области пространства, существенной для распространения радиоволн. 3) исследование дифракции на плоском экране. 4) исследование дифракции на щелях разной ширины. 2 Краткие теоретические сведения В основе скалярной теории дифракции и дальнейших уточнений этой теории лежит принцип Гюйгенса. Согласно этому принципу, каждая точка волновой поверхности рассматривается как источник сферических волн и новая волновая поверхность является огибающей этих волн. Математической формулировкой этого принципа является формула Кирхгофа.  (2.1) (2.1)Выражение e-jkr /r − в формуле Кирхгофа называется функцией Грина свободного пространства и представляет поля воображаемых точечных источников, если бы они находились в точках поверхности. Формулу Кирхгофа можно считать точной, если известно распределение поля US0 на поверхности S0. Однако на практике это поле, как правило, бывает неизвестно. В качестве приближенного значения US0 обычно используют приближение Кирхгофа, согласно которому поле на отверстиях в плоскости S0 предполагается невозмущенным, т.е. таким, как если бы никаких экранов в этой плоскости не было, а поле на экранах со стороны точки наблюдения равным нулю. В действительности токи, затекающие на теневую (противоположную от источника) сторону экрана, также создают поле в точке наблюдения, как и отверстия в экране, а поле на отверстиях искажается этими токами. Приближение Кирхгофа дает удовлетворительные результаты, если размеры отверстия значительно больше длины волны, так как поле на отверстиях становится невозмущенным. Френель в 1818 году предложил наглядный способ оценки интеграла, входящего. Для этого поверхность S0 мысленно делится на области, называемые теперь зонами Френеля (рисунок 2.1). 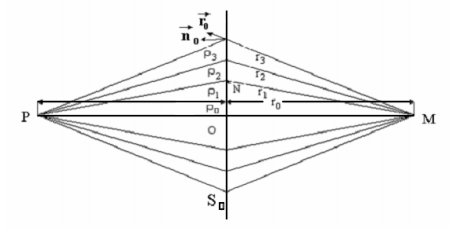 Рисунок 2.1 – Зоны Френеля Границы зон Френеля на поверхности S0 определяются из условия, что длина пути волны (r + ρ) увеличивается на λ/2 при переходе к последующей зоне. Таким образом, поле в точке наблюдения определяется суммированием полей от различных зон Френеля. 3Описание экспериментальной установки Установка, представленная на рисунке 3.1, состоит из высокочастотного генератора Г4-155(1); передающей (2) и приемной (5) антенн-рупоров; каретки (3), двигающейся по рельсам (4), детекторной секции (6) с амперметром (7).  Рисунок 2.1 – Схема экспериментальной установки На рисунке 2.2 изображены узлы экспериментальной установки: каретка 3, с укрепленным на ней деревянным экраном 5 и зонами Френеля 6. Положение каретки 3 фиксируется с помощью укрепленного на ней указателя 2 и отсчетной линейки 1.  Рисунок 2.2 – Узлы экспериментальной установки 4 Основные расчетные формулы Формула расчета радиуса n-й зоны Френеля:  , (4.1) , (4.1)где  – номер зоны Френеля; – номер зоны Френеля; – длинна волны; – длинна волны;  Модуль коэффициента ослабления поля:  (4.2) (4.2)где  – интегралы Френеля. – интегралы Френеля.Интегралы Френеля:  (4.3) (4.3)5 Результаты работы и их анализ В первом этапе данной лабораторной работы перед источником устанавливалось препятствие в виде колец с радиусами, равными радиусам соответствующих зон Френеля. Поочередно кольца снимались, тем самым увеличивая количество открытых зон Френеля, на приемнике снималось значение уровня напряжения. Результаты представлены в виде таблицы 5.1 и рисунка 5.1.  Рисунок 5.1 – Уровень сигнала от количества открытых зон. Длина волны (см) = 1,1. Расстояние между антеннами (см) = 153,2.
Таблица 5.1 – Уровень сигнала от количества открытых зон. Зависимость уровня напряжения на приемнике от открытия только чётных зон представлена в таблице 5.2 и рисунке 5.2.  Рисунок 5.2 – Уровень сигнала от количества открытых четных зон. Длина волны (см) = 1,1. Расстояние между антеннами (см) = 153,2.
Таблица 5.2 – Уровень сигнала от количества открытых четных зон. Зависимость уровня напряжения на приемнике от открытия только нечётных зон представлена в таблице 5.3 и рисунке 5.3.  Рисунок 5.3- Уровень сигнала от количества открытых нечетных зон. Длина волны (см) = 1,1. Расстояние между антеннами (см) = 153,2.
Таблица 5.3 – Уровень сигнала от количества открытых нечетных зон. Во втором этапе данной лабораторной работы проводилось измерение уровня напряжения на приемнике при изменении расположения источника при дифракции на краю экрана. Результаты измерений представлены в таблице 5.4 и рисунке 5.4:  Рисунок (5.4)- Уровень Um от смещения X.
Таблица (5.4) – Уровень Um от смещения X. В третьем этапе данной лабораторной работы изменялось расстояние между источником и экраном X, измерялось значение радиуса первой зоны Френеля. Результаты измерений представлены в таблице 5.5 и рисунке 5.5:  Рисунок (5.5) – Существенная область распространения
Таблица (5.5) – Существенная область распространения. В четвертом этапе данной лабораторной работы изменялось расположение источника относительно щели, измерялось значение напряжения на приёмнике. Данные измерения проводились также для узкой и широкой щели. Результаты измерений представлены в таблице 5.6 и рисунке 5.6:  Рисунок (5.5) – Зависимость поля от смещения детектора
Таблица (5.5) – Зависимость поля от смещения детектора Выводы При открытии двух соседних зон Френеля значение сигнала практически равно нулю. Это связано с тем, расстояние от двух соседних волн до точки наблюдения отличается на половину длины волны, и, как следствие, эти волны находятся в противофазе. При этом видно, что, если открывать только нечетные или четные зоны, значение сигнала возрастает. Однако, каждая последующая открытая зона вносит все меньший вклад. При постепенном закрытии точки наблюдения, значение сигнала уменьшается, в то время, как при постепенном открытии, открываются зоны Френеля. При узкой щели значение сигнала изменяется почти монотонно, что связано с тем, что на щели укладывается только часть первой зоны Френеля. При широкой щели наблюдаются колебания, что связано с тем, что изначально проходят большее количество зон Френеля и при из закрытии наблюдается уменьшение или увеличение значения сигнала. |
