Надежность технических систем. Практическая.. Практичесоке задание 1. Отчет по выполнению практического задания 1 по дисциплине Надежность технических систем

• Название: Отчет по выполнению практического задания 1 по дисциплине Надежность технических систем
• Анкор: Надежность технических систем. Практическая
• Дата: 04.10.2022
• Размер: 29.13 Kb.
• Имя файла: Практичесоке задание 1.docx
• Тип: Отчет; #713498

Министерство науки и высшего образования Республики Казахстан

ВОСТОЧНО-КАЗАХСТАНСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ.Д.СЕРИКБАЕВА

Школа информационных технологий и интеллектуальных систем

ОТЧЕТ

по выполнению практического задания 1

по дисциплине «Надежность технических систем»

Вариант № 3

Выполнил:

студент группы 21-аут-3

специальности 6В07101 «Автоматизация и управление»

Глухов Дмитрий Алексеевич
Проверил:

ассоциированный профессор ШИТиИС, PhD Григорьева С.В.

Усть-Каменогорск, 2022

Задание 1

Допустим, что на испытание поставлено 3000 однотипных электронных ламп. За первые 1000 ч отказало 120 ламп, а за интервал времени 1000 – 2000 ч отказало еще 70 ламп. Требуется определить частоту f(t) и интенсивность λ(t) отказов электронных ламп в промежутке времени t=1000 – 2000 ч.

Дано:

N = 3000 шт.

t₁ = 1000 ч.

n₁ = 120 шт.

t₂ = [1000, 2000] ч.

n₂ = 70 шт.
Найти:

f(∆t)

λ(∆t)
Решение: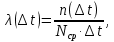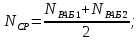











Где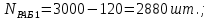











Ответ:

Частота отказов электронных ламп: , .

Интенсивность отказов электронных ламп: ,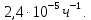

Задание 2

В течение времени t производилось наблюдение за восстанавливаемым изделием, и было зафиксировано n(t) =4 отказа. До начала наблюдения изделие проработало в течение времени t₁=2200 ч, общее время наработки к концу наблюдения составило t₂=6320 ч. Требуется найти наработку на отказ.

Найти:_t_ср_Решение'>Дано:

t₁ = 2200 ч.

t₂ = 6320 ч.

n(t) = 4
Найти:

t_ср

Решение:

Найдем наработку изделия за наблюдаемый период.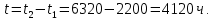



Принимая -

Находим среднюю наработку на отказ: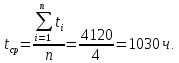



Где

t_i – время исправной работы изделия между (i – 1) и i – м отказами;

n – число отказов за некоторое время t.

Ответ:

Наработка на отказ равна 1030 ч.

Задание 3

Система состоит из 4 приборов, причем отказ любого одного из них ведет к отказу системы. Известно, что первый отказал 15 раз в течение 780 ч работы, второй – 22 раза в течение 812 ч работы, третий – 18 раз в течение 456 ч работы, а четвертый – 7 раз в течение 260 часов работы. Определить наработку на отказ системы в целом, если справедлив экспоненциальный закон надежности для каждого из четырех приборов.

Дано:

N = 4 шт.

n₁ = 15 шт.

n₂ = 22 шт.

n₃ = 18 шт.

n₄ = 7 шт.

t₁ = 780 ч.

t₂ = 812 ч.

t₃ = 456 ч.

t₄ = 260 ч.
Найти:
t_ср
Решение:

Используется следующие соотношения:



Определяется интенсивность отказов для каждого прибора (N = 1):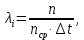



Где N_ср – среднее число исправно работающих изделий

в интервале ∆t.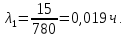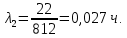






Тогда интенсивность отказов системы будет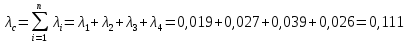



Средняя наработка на отказ системы равна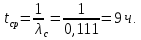


Ответ:

Наработка на отказ в системы в целом, учитывая экспоненциальный закон надежности для каждого из четырех приборов равен 9 ч.

Задание 4

Дано.

Время безотказной работы гироскопического устройства с шарикоподшипниками в осях ротора гироскопа подчиняется закону


0
Вейбулла-Гнеденко с параметрами k=2,3; λо 0,5 10^4 ч^-1, а время его

работы t=800 ч. Вычислить количественные характеристики надежности такого устройства.

Дано:

k = 2,3

λ₀ = 0,5 ∙ 10^-4 ч^-1

t = 800 ч.

Найти:

P(t)

𝑓(t)

λ(t)

t_ср
Решение:

Используются формулы закона Вейбулла – Гнеденко для определения количественных характеристик. Определяется вероятность безотказной работы: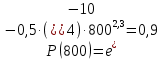





Частота отказов определяется по формуле



Тогда



Интенсивность отказов определяется по формуле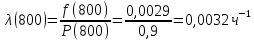





Вычисляется средняя наработка до первого отказа



Сначала вычисляют значение гамма-функции, воспользовшись справочными данными:



Значение гамма-функции

x	Г(х)
1,67	0,90330

Полученные значения подставляем в формулу: