Практическая 4 Гусаров. Отчет по выполнению практического задания
 Скачать 251.36 Kb. Скачать 251.36 Kb.
|
bstree() { clear(); } МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «МИРЭА – Российский технологический университет» РТУ МИРЭА  Отчет по выполнению практического задания Тема: Сбалансированные деревья поиска (СДП) и их применение для поиска данных в файле. Дисциплина: Структуры и алгоритмы обработки данных Выполнил студент Гусаров М.К.  группа ИКБО-18-21  ФамилияИ.О . Москва 2022 bstree(const bstree&) = delete; bstree& operator = (const bstree&) = delete; public: //добавить void add(const T& v) { node* p; if (tr == nullptr) { tr = new node(); tr->val = v; } else { node** rp = _find(v); if (tr != nullptr) { p = new node(); p->val = v; *rp = p; } } } void add(T&& v) { node* p; if (tr == nullptr) { tr = new node(); tr->val = std::forward } else { node** rp = _find(v); if (tr != nullptr) { p = new node(); p->val = std::forward *rp = p; } } } //удаление с возвращением min-значения T pop_min(void) noexcept { T v; node** rp = &tr, * p = tr; if (tr != nullptr) { while (p->left != nullptr) { rp = &p->left; p = p->left; } } if (p != nullptr) { v = std::forward _erase(rp, p); } return std::forward } //удаление с возвращением max-значения T pop_max(void) noexcept { T v; node** rp = &tr, * p = tr; if (tr != nullptr) { while (p->right != nullptr) { rp = &p->right; p = p->right; } } if (p != nullptr) { v = std::forward _erase(rp, p); } return std::forward } //удаление всех void clear(void) noexcept { _clear(tr); tr = nullptr; } bool empty(void) const noexcept { return (tr == nullptr); } private: node** _find(const T& v) noexcept { node** rp = &tr, * p = tr; while (p != nullptr) { if (v == p->val) return nullptr; else if (v < p->val) { rp = &p->left; p = p->left; } else { rp = &p->right; p = p->right; } } return rp; } void _erase(node** rp, node* p) noexcept { if (p->right == nullptr) *rp = p->left; else { node* t = p->right; if (t->left == nullptr) { t->left = p->left; *rp = t; } else { node* i = t->left; while (i->left != nullptr) { t = i; i = t->left; } t->left = i->right; i->left = p->left; i->right = p->right; *rp = i; } } delete p; } void _clear(node* p) noexcept { if (p != nullptr) { if (p->left != nullptr) _clear(p->left); if (p->right != nullptr) _clear(p->right); delete p; } } }; /* чтение массива данных из строки, консоли или файла N = кол-во элементов данные ... */ template void get_array(std::vector T v; size_t n; if (!(_in >> n) || !n) return; vs.resize(n); for (size_t i = 0; i < n; ++i) { if (!(_in >> vs[i])) break; } } int main(void) { std::vector //сортировка целых чисел std::vector /* ввод из консоли get_array // для примера ввод из строки char s[] = "10\n5 4 7 9 8 2 1 3 0 6"; std::istringstream sp(s); get_array bstree for (auto v : ia) ti.add(v); for (i = 0; !ti.empty(); ++i) ia[i] = ti.pop_min(); for (auto v : ia) std::cout << v << ' '; std::cout << std::endl; //сортировка строк std::vector //ввод из строки char s1[] = "7\nALLAH\nSHARIAT\nEBALROT\nSOSIXUI\nPIDORAS\nALGOL\nBASIC"; std::istringstream sp1(s1); get_array bstree for (i = 0; i < sa.size(); ++i) ts.add(std::move(sa[i])); for (i = 0; !ts.empty(); ++i) sa[i] = ts.pop_min(); for (const auto& v : sa) std::cout << v << ' '; std::cout << std::endl; //сортировка действительных чисел по убыванию std::vector /* ввод из файла std::ifstream fp("file.txt"); get_array fp.close(); */ //для примера из строки char s2[] = "5\n 0.9 20.5 -123.1 0.5 4.4"; std::istringstream sp2(s2); get_array bstree for (const auto& d : da) td.add(d); for (i = 0; !td.empty(); ++i) da[i] = td.pop_max(); for (const auto& v : da) std::cout << v << ' '; std::cin.get(); return 0; } 3 Тестирование программы – задание 1 Рисунок 1 – Тестирование программы – задание 1 4 Задание - 2Постановка задачиРазработать приложение, которое использует сбалансированное дерево поиска, предложенное в варианте, для доступа к записям файла.1. Разработать класс СДП с учетом дерева варианта. Структура информационной части узла дерева включает ключ и ссылку на запись в файле (адрес места размещения). Основные методы: включение элемента в дерево; поиск ключа в дереве с возвратом ссылки; удаление ключа из дерева; вывод дерева в форме дерева (с отображением структуры дерева). 2. Разработать приложение, которое создает и управляет СДП в соответствии с заданием.3. Выполнить тестирование.4. Определить среднее число выполненных поворотов (число поворотов на общее число вставленных ключей) при включении ключей в дерево при формировании дерева из двоичного файла.5. Оформить отчет6. Варианты индивидуальных заданий задания 2Таблица 1 – вариант упражнений
5 Код реализации программы – задание 2#include #include #include class baza{ public: static std::vector < std::string > string_split( std::string s, std::string delimiter) { size_t pos_start = 0; size_t pos_end; size_t delim_len = delimiter.length(); std::string token; std::vector < std::string > res; while ((pos_end = s.find(delimiter, pos_start)) != std::string::npos) { token = s.substr(pos_start, pos_end - pos_start); pos_start = pos_end + delim_len; res.push_back(token); } res.push_back(s.substr(pos_start)); return res; } }; class Node { public: long key; int address; Node* parent; Node* left; Node* right; Node(long key, int address) { this->key = key; this->address = address; this->parent = nullptr; this->left = nullptr; this->right = nullptr; } }; class SplayTree { public: static void main(std::vector { SplayTree* tree = new SplayTree(); tree->insertFromFile(); tree->output(); std::cout << "\n" << std::endl; std::cout << "Adress nomera 89627156421 v fajle = " + std::to_string(tree->searchTree(89627156421l)->address) << std::endl; tree->output(); std::cout << "\n" << std::endl; tree->deleteNode(89827421497l); tree->deleteNode(89359172451l); tree->deleteNode(89268725389l); tree->deleteNode(89266715862l); // otsutstvuet v dereve tree->output(); std::cout << "\n" << std::endl; tree->deleteNode(89266715863l); tree->output(); std::cout << "\n" << std::endl; std::cout << ru::luckoff::SplayTree::SplayTree::searchInFileByAddress(tree->searchTree(89627156421l)->address) << std::endl; } static std::string searchInFileByAddress(int address) throws FileNotFoundException { std::string FILE_NAME = "Tree.txt"; File file = java.io.File(FILE_NAME); FileInputStream inputStream = java.io.FileInputStream(file); try (BufferedReader br = java.io.BufferedReader(java.io.InputStreamReader(inputStream));) { std::string line; while ((line = br.readLine()) != nullptr) { if (Settlement::string_split(line, " ")[0].equalsIgnoreCase(to_string(address))) { return line; } } } catch (IOException e) { e.printStackTrace(); } return nullptr; } void insertFromFile() throws FileNotFoundException { std::string FILE_NAME = "Tree.txt"; File file = java.io.File(FILE_NAME); FileInputStream inputStream = java.io.FileInputStream(file); try (BufferedReader br = java.io.BufferedReader(java.io.InputStreamReader(inputStream));) { std::string line; while ((line = br.readLine()) != nullptr) { int address = stoi(Settlement::string_split(line, " ")[0]); long key = long long.parseLong(Settlement::string_split(line, " ")[1]); this->insert(key, address); } } catch (IOException e) { e.printStackTrace(); } } private: Node* root; public: SplayTree() { root = nullptr; } void output() { outputHelper(this->root, 0); } void outputHelper(Node*& node, int l) { if (node != nullptr) { outputHelper(node->right, l + 1); for (int i = 1; i <= l; i++) { std::cout << " "; } std::cout << std::to_string(node->key) + "\n"; outputHelper(node->left, l + 1); } } Node* searchTree(long k) { Node* x = searchTreeHelper(root, k); if (x != nullptr) { splay(x); } return x; } private: Node* searchTreeHelper(Node*& node, long key) { if (node == nullptr || key == node->key) { return node; } if (key < node->key) { return searchTreeHelper(node->left, key); } return searchTreeHelper(node->right, key); } public: void deleteNode(long data) { deleteNodeHelper(this->root, data); } private: void deleteNodeHelper(Node*& node, long key) { Node* x = nullptr; Node* t = nullptr; Node* s = nullptr; while (node != nullptr) { if (node->key == key) { x = node; } if (node->key <= key) { node = node->right; } else { node = node->left; } } if (x == nullptr) { std::cout << "Klyuch " + std::to_string(key) + " otsutstvuet v dereve" << std::endl; return; } splay(x); if (x->right != nullptr) { t = x->right; t->parent = nullptr; } else { t = nullptr; } s = x; s->right = nullptr; x = nullptr; if (s->left != nullptr) { // remove x s->left->parent = nullptr; } root = join(s->left, t); s = nullptr; } void leftRotate(Node*& x) { Node* y = x->right; x->right = y->left; if (y->left != nullptr) { y->left->parent = x; } y->parent = x->parent; if (x->parent == nullptr) { this->root = y; } else if (x == x->parent->left) { x->parent->left = y; } else { x->parent->right = y; } y->left = x; x->parent = y; } void rightRotate(Node*& x) { Node* y = x->left; x->left = y->right; if (y->right != nullptr) { y->right->parent = x; } y->parent = x->parent; if (x->parent == nullptr) { this->root = y; } else if (x == x->parent->right) { x->parent->right = y; } else { x->parent->left = y; } y->right = x; x->parent = y; } void splay(Node*& x) { while (x->parent != nullptr) { if (x->parent->parent == nullptr) { if (x == x->parent->left) { // zig rotation rightRotate(x->parent); } else { // zag rotation leftRotate(x->parent); } } else if (x == x->parent->left && x->parent == x->parent->parent->left) { // zig-zig rotation rightRotate(x->parent->parent); rightRotate(x->parent); } else if (x == x->parent->right && x->parent == x->parent->parent->right) { // zag-zag rotation leftRotate(x->parent->parent); leftRotate(x->parent); } else if (x == x->parent->right && x->parent == x->parent->parent->left) { // zig-zag rotation leftRotate(x->parent); rightRotate(x->parent); } else { // zag-zig rotation rightRotate(x->parent); leftRotate(x->parent); } } } Node* join(Node*& s, Node*& t) { if (s == nullptr) { return t; } if (t == nullptr) { return s; } Node* x = maximum(s); splay(x); x->right = t; t->parent = x; return x; } public: Node* maximum(Node*& node) { while (node->right != nullptr) { node = node->right; } return node; } void insert(long key, int address) { Node* node = new Node(key, address); Node* y = nullptr; Node* x = this->root; while (x != nullptr) { y = x; if (node->key < x->key) { x = x->left; } else { x = x->right; } } node->parent = y; if (y == nullptr) { root = node; } else if (node->key < y->key) { y->left = node; } else { y->right = node; } splay(node); } }; int main(int argc, char** argv) { std::vector SplayTree::main(parameter); return 0 6 Тестирование программы – задание 2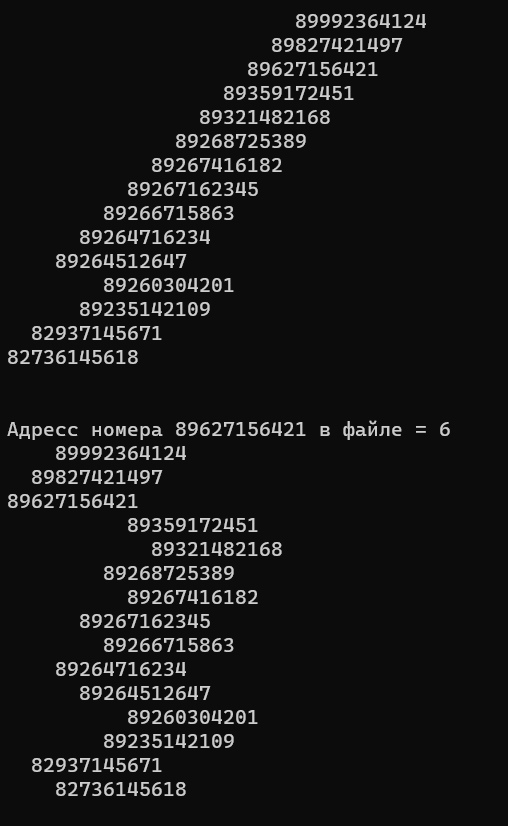 Рисунок 2 – Тестирование программы – задание 2 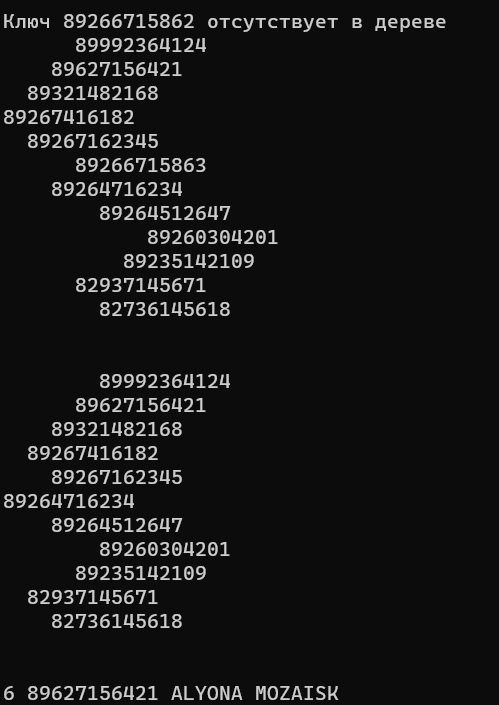 Рисунок 3 – Тестирование программы – задание 2 7 ВыводВ ходе работы над практической работой было изучена работа с сбалансированными деревьями поиска, а также были получены умения и навыки: - разработки и реализации алгоритмов управления бинарными деревьями поиска и сбалансированными бинарными деревьями поиска -применение файловых потоков прямого доступа к данным файла -применение сбалансированного дерева поиска для прямого доступа к записям фала 8 Список литературыСправочная информация программы Microsoft Visual Studio 2019. Лекции по структуре и алгоритмах обработки данных(СиАОД) / Макеева О.В.– Москва, РТУ МИРЭА, 2022. |
