Э-10-19 РыжоваАК ТР5. Переходные процессы в однородных длинных линиях без потерь
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
|
Министерство науки и высшего образования РФ  Кафедра ТЕОРЕТИЧЕСКИХ ОСНОВ ЭЛЕКТРОТЕХНИКИ Типовой расчет №1 «Переходные процессы в однородных длинных линиях без потерь» Выполнил: Рыжова А.К. Проверил: Силаев М.А. Группа: Э-10-19 Вариант:21 Москва, 2021 1. Выписать из таблицы в соответствии с вариантом n значения параметров линий, элементов 1, 2, 3 и нагрузки. Начертить схему цепи рис. 1 с учётом общепринятых обозначений элементов R, L, C. Указать на схеме численные значения всех параметров Исходные данные:  (рис.1 Исходные данные) N=10; n=21 L1=60км; Zc1=8R=480 Ом; V1=3*105 км/с; L2=0,5L1=30км ; V2=1,5*105 км/с; Zc2=1,5R=90 Ом U0=10N=10*10=100 кВ R0=25+N=25+10=35 Ом R=50+N=50+10=60 Ом L=20 мГн; С=0,5 мкФ tp= 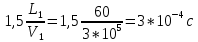 2. Получить аналитические выражения и построить графики распределения прямых, обратных волн и результирующих напряжений и токов вдоль линий для момента времени после замыкания рубильника 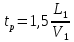 1.Расчет докоммутационного режима: 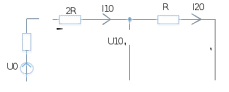 (рис.2 схема до коммутации) I10=I20=0 U20=0; Uруб=U10=U0=100кВ=100000В 2. 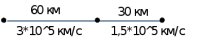 (рис.3) t1=  Δt1=tp-t1=3*10-4-2*10-4=1*10-4 c L1пр=V1* Δt1=3*105*1*10-4=30км t2= 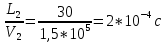 Δt2=tp-t2=3*10-4-2*10-4=1*10-4 c L2обр=V2* Δt2=1,5*105*1*10-4=15км 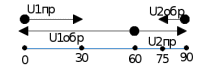 (рис.4 Распределение прямых и обратных волн) U1(x)= 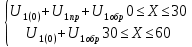 U2(x)= U2(x)=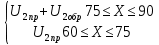 i1(x)= 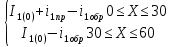 i2(x)= i2(x)=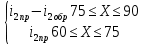 3.Приведем к ННУ: 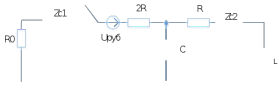 (рис.5 схема с независимыми начальными условиями)  (рис.6 расчетная схема) ННУ: Uc(0)=0 i2пр(t)= i2пр прин(t)+ i2пр своб(t) i1обр(t)= i1обр прин(t)+ i1обр своб(t) Принужденный режим(установившийся) 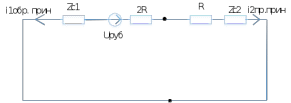 (рис.7 установившийся режим) i2пр прин(t)= -i1обр прин(t) i2пр прин(t)=  i1обр прин(t)=-133.3А  (рис.8 схема для расчета входного сопротивления) Zвх(p)=0 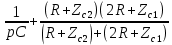 =0 =0= 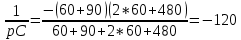 p=  i2пр(t)=133,3+Ае-16667t А (1) i2пр(0)=133,3+А i1обр(t)=-133,3+Ве-16667t А (2) i1обр(0)=-133,3+В ЗНУ(после коммутации) 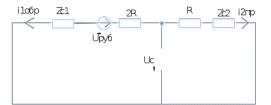 (рис.9 схема после коммутации) 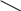 -i1обр(2R+Zc1)+Uc(0)=Uруб ↔ i1обр= -i1обр(2R+Zc1)+Uc(0)=Uруб ↔ i1обр=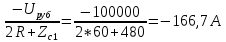 i2пр=0 А=0-133,3=-133,3 В=-166,7+133,3=-33,4 Подставляем найденные значения A и Bв формулы (1) и (2): i2пр(t)=133,3-133,3e-16667t A i1обр(t)=-133,3-33,4e-16667t A U2пр= i2пр*Zc2=(133,3-133,3e-16667t) *90=11997-11997e-16667t B U1обр= i1обр* Zc1=(-133,3-33,4e-16667t)*480=-63984-16032e-16667t B Линия 1: 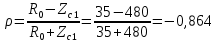 i1пр=ρ* i1обр=-0,864*(-133,3-33,4e-16667t)=115,17+28,86e-16667t A U1пр= ρ* U1обр=-0,864*(-63984-16032e-16667t)=55282,18+13851,65e-16667t B Линия 2:  (рис.10) ННУ: iL=0 Zвх(p)=0 pL+Zc2=0 ↔ p= 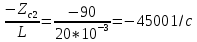 2U2пр(t)=23994-23994e-16667t B 2U2пр(p)≡  I2(p)= 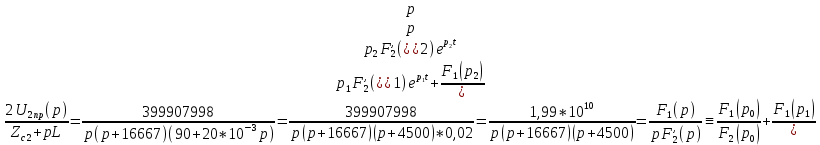 p0=0; p1=-16667 1/с; p2=-4500 1/с 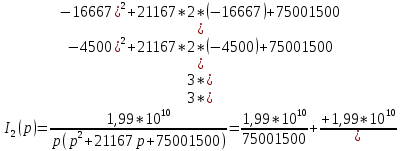 А АI2(p)=i2; i2= i2пр- i2обр i2обр= i2пр- i2=133,3-133,3e-16667t-265,3+363,5e-4500t-98,1e-16667t= =-132-231,4e-16667t+363,53e-4500t A U2обр=ρ*U2пр 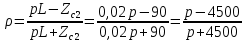 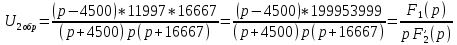 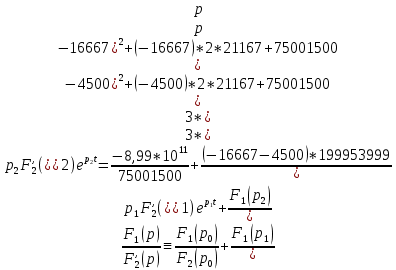 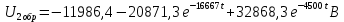 Запишем выражения с зависимостью от координаты: 1 линия: 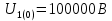 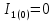  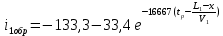 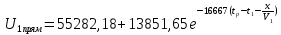 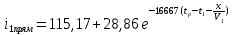 2 линия: 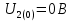  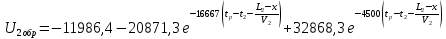  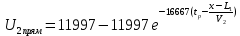 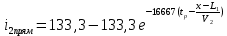 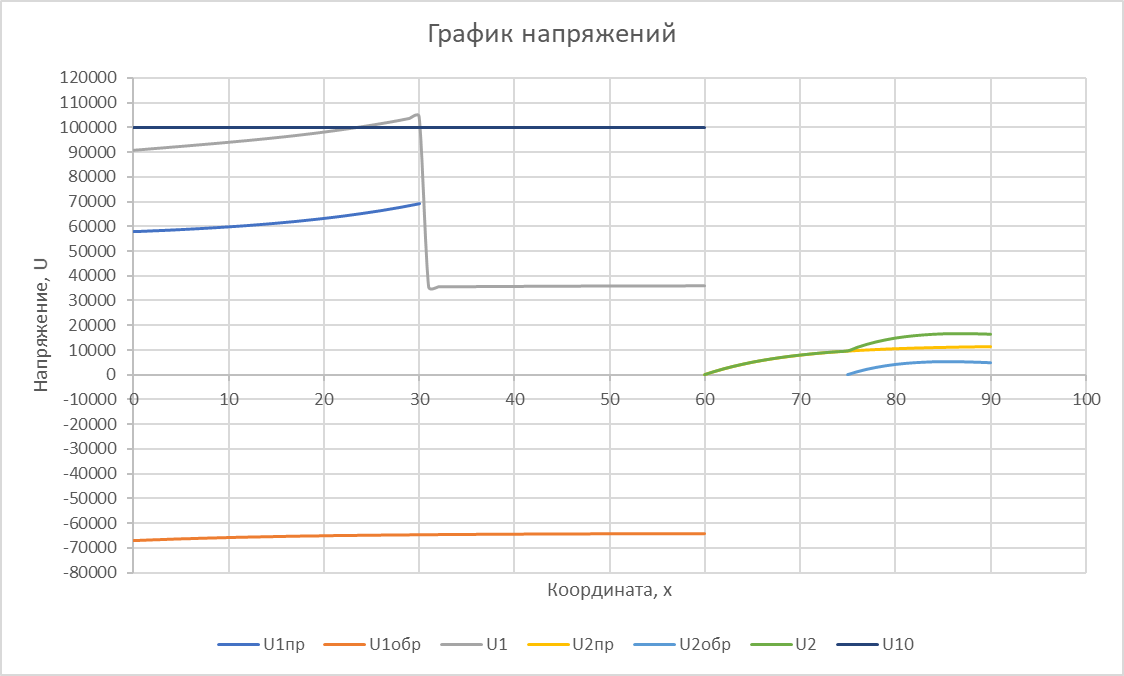 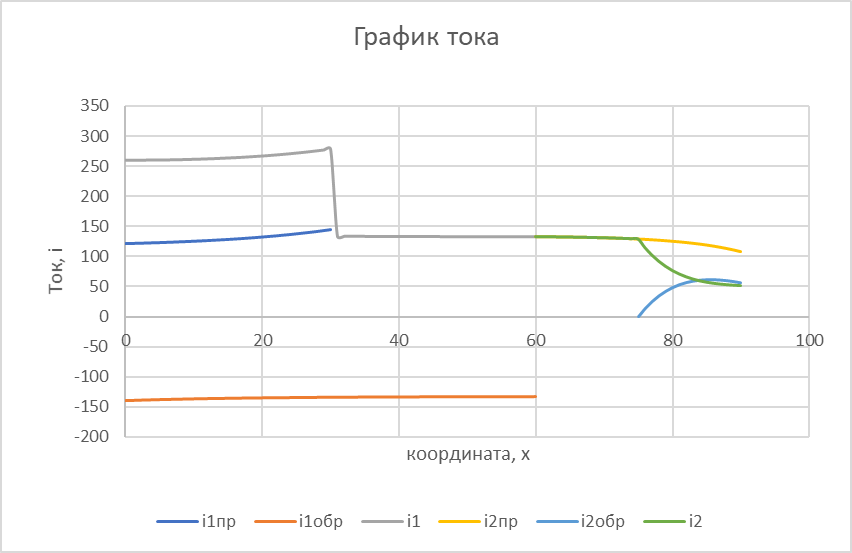 3. Записать аналитические выражения и построить графики зависимости напряжения и тока от времени (t ≤ tp) в конце второй линии (на нагрузке). На нагрузке встречаются и прямые, и обратные волны, тогда t2≤t≤tp 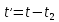 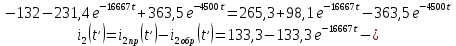 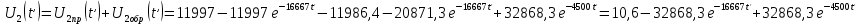 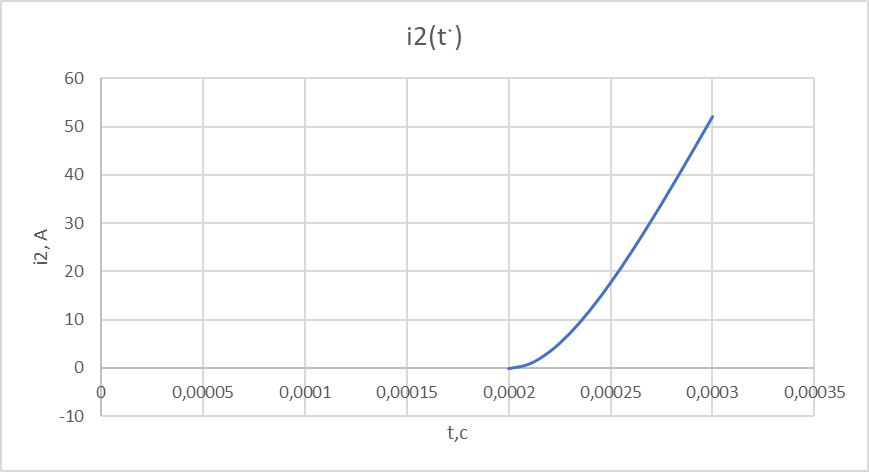  |
