Перевод чисел из десятичной системы счисления в 2ю,8ю,16ю.
 Скачать 18.22 Kb.
|
|
Практическая работа № 10 Тема: «Перевод чисел из десятичной системы счисления в 2-ю,8-ю,16-ю.» УД: Информатика Дата: 22.09.2020 Цель: научиться переводит различные дробные числа из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную. Выполнил: Щербинина Ирина Андреевна Группа: 14 гр. Специальность: 09.02.07 Информационные системы и программирование Преподаватель: Дураков Сергей Геннадьевич ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И ФОРМА ОТЧЕТНОСТИ. Задание 1. Написать сжатый (план) конспект, по теме используя раздел теория. Перевод целых чисел. Если снование q - ичной системы счисления является степенью числа 2,то перевод чисел q - ичной системы счисления в двоичную и обратно можно проводить по более простым правилам. Для этого чтобы целое двоичное число записать в системе счисления с основанием q= 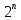 , нужно:1. Двоичное число разбить справа налево на группы по n цифр в каждой. 2. Если в последней левой группы окажется меньше n разрядов, то её надо дополнить слева нулями до нужного числа разрядов. 3. Рассмотреть каждую группу как n-разрядное двоичное число и записать её соответствующей цифрой в системе счисления с основанием q= 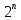Перевод дробных чисел. Для того, чтобы дробное двоичное число записать в системе счисления с основанием q= 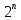, нужно:Двоичное число разбить слева направо на группы по n цифр в каждой. Если в последней правой группы окажется меньше n разрядов, то её надо дополнить справа нулями до нужного числа разрядов. Рассмотреть каждую группу как n – разрядное двоичное число и записать её соответствующей цифрой в системе счисления с основанием q= 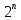.Перевод произвольных чисел. Для того чтобы произвольное двоичное число записать в системе счисления с основанием q= 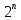,нужно:Целую часть данного двоичного числа разбить справа налево, а дробную – слева направо на группы по n цифр в каждой. Если в последней левой и/ или правой группах окажется меньше n разрядов, то их надо дополнить слева и / или справа нулями до нужного числа разрядов. 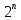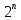Рассмотреть каждую группу как n – разрядное двоичное число и записать её соответствующей цифрой в системе счисления с основанием q = Перевод чисел из систем счисления с основанием q= в двоичную систему. Для того, чтобы произвольное число , записанное в системе счисления с основанием q=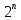 , перевести в двоичную систему счисления, нужно каждую цифру этого числа заменить её n – значным эквивалентом в двоичной системе счисления. Задание 2. Ответить на контрольные вопросы письменно. Сделать вывод. КОНТРОЛЬНЫЕ ВОПРОСЫ: 1. Сформулируйте правило перевода произвольных чисел и приведите примеры перевода чисел используя сформулированное правило. Перевод произвольных чисел. Для того чтобы произвольное двоичное число записать в системе счисления с основанием q= 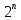,нужно:Целую часть данного двоичного числа разбить справа налево, а дробную – слева направо на группы по n цифр в каждой. Если в последней левой и/ или правой группах окажется меньше n разрядов, то их надо дополнить слева и / или справа нулями до нужного числа разрядов. Рассмотреть каждую группу как n – разрядное двоичное число и записать её соответствующей цифрой в системе счисления с основанием q = 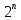 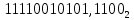= 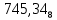2. Сформулируйте правило перевода чисел из систем счисления с основанием 2 в системы счисления с основанием 8 и 16. Перевод целых чисел. Если снование q - ичной системы счисления является степенью числа 2,то перевод чисел q - ичной системы счисления в двоичную и обратно можно проводить по более простым правилам. Для этого чтобы целое двоичное число записать в системе счисления с основанием q= 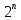, нужно:Двоичное число разбить справа налево на группы по n цифр в каждой. Если в последней левой группы окажется меньше n разрядов, то её надо дополнить слева нулями до нужного числа разрядов. Рассмотреть каждую группу как n-разрядное двоичное число и записать её соответствующей цифрой в системе счисления с основанием q= 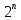3. Приведите примеры перевода чисел, используя сформулированное правило в контрольном вопросе 2. 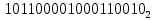 =  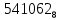 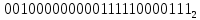= Задание 3. Решите задачи, для самостоятельного решения. Составить отчет по работе.
|