МАТАН-Лекция2. Плоскость и прямая в пространстве Уравнения плоскости
 Скачать 319.72 Kb. Скачать 319.72 Kb.
|
|
Плоскость и прямая в пространстве Уравнения плоскости Уравнение плоскости, проходящей через данную точку и имеющей данный нормальный вектор. Пусть в пространстве задана точка M0(x0; y0; z0) и вектор 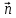 = {A; B; C}. Плоскость, проходящая через точку M0(x0; y0; z0) и перпендикулярная к ненулевому вектору = {A; B; C}. Плоскость, проходящая через точку M0(x0; y0; z0) и перпендикулярная к ненулевому вектору 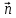 (нормальному вектору) представляется следующим уравнением: (нормальному вектору) представляется следующим уравнением:A(x - x0) + B(y - y0) + C(z - z0) = 0. Это уравнение отражает тот факт, что вектор 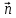 ортогонален любому вектору ортогонален любому вектору  на плоскости. Точка M(x; y; z) – произвольная точка плоскости. на плоскости. Точка M(x; y; z) – произвольная точка плоскости. Общее уравнение плоскости имеет следующий вид: Ax + By + Cz + D = 0.  Уравнение плоскости, проходящей через три заданные точки. Пусть в пространстве заданы три точки M1(x1; y1; z1), M2(x2; y2; z2), M3(x3; y3; z3) не лежащие на одной прямой. Проходящая через них плоскость представляется уравнением  = 0. = 0.Это уравнение отражает компланарность векторов  , ,  , ,  . Точка M(x; y; z) – произвольная точка плоскости. . Точка M(x; y; z) – произвольная точка плоскости. Уравнение плоскости в отрезках. Пусть плоскость проходит через три точки A(a; 0; 0), B(0; b; 0), C(0; 0; c), отсекая на координатных осях не равные нулю отрезки a, b, c. Тогда ее уравнение имеет вид  + +  + +  = 1. = 1. Нормальное уравнение плоскости: x  + y + y + z + z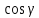 - p = 0, - p = 0,где  , ,  , , 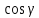 - направляющие косинусы нормального вектора плоскости - направляющие косинусы нормального вектора плоскости 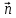 ; ;p – расстояние от начала координат до плоскости. Считается, что вектор 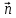 направлен от начала координат к плоскости (начало вектора направлен от начала координат к плоскости (начало вектора 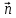 связывают с началом координатной системы и смотрят его направление – к плоскости или от плоскости). Это уравнение отражает тот факт, что проекция вектора, проведенного из начала О в произвольную точку плоскости, всегда равна значению p. связывают с началом координатной системы и смотрят его направление – к плоскости или от плоскости). Это уравнение отражает тот факт, что проекция вектора, проведенного из начала О в произвольную точку плоскости, всегда равна значению p. Общее уравнение плоскости Ax + By + Cz + D = 0 приводится к нормальному виду умножением на нормирующий множитель  = =  . Знак нормирующего множителя берется противоположным знаку свободного члена D в общем уравнении плоскости. . Знак нормирующего множителя берется противоположным знаку свободного члена D в общем уравнении плоскости.Пример. Составить общее уравнение плоскости, проходящей через точку P(-1; 2; 2), параллельно векторам  = {2; -2; 3} и = {2; -2; 3} и  = {4; 1; 5}. = {4; 1; 5}.Решение. Вначале находим нормальный вектор 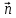 искомой плоскости по формуле искомой плоскости по формуле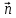 = =   = =  = =  - -  + +  = - 13 = - 13 + 2 + 2 + 10 + 10 . .Получили, что 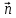 = {-13; 2; 10}. = {-13; 2; 10}. Теперь составим уравнение плоскости, которая проходит через заданную точку P и перпендикулярна вектору 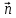 : :-13(x + 1) + 2(y – 2) + 10(z – 2) = 0. Отсюда находим общее уравнение искомой плоскости: -13x + 2y + 10z – 37 = 0. Угол между плоскостями. Под углом между плоскостямипонимается один из двугранных углов, образованный этими плоскостями (либо острый, либо тупой).  Пусть плоскости заданы своими общими уравнениями (Q1): A1x + B1y + C1z + D1 = 0 ; (Q2): A2x + B2y + C2z + D2 = 0. За угол  между плоскостями(Q1) и (Q2) принимается угол между нормальными векторами плоскостей между плоскостями(Q1) и (Q2) принимается угол между нормальными векторами плоскостей 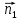 = {A1; B1; C1} и = {A1; B1; C1} и  = {A2; B2; C2} и его косинус находится по формуле = {A2; B2; C2} и его косинус находится по формуле = =  = =  . .Условие ортогональности двух плоскостей. Если плоскость (Q1) ортогональна плоскости (Q2), то их нормальные векторы будут также ортогональны, а тогда  = 0 и = 0 и  = 0. = 0.Условие параллельности двух плоскостей. Если плоскость (Q1) параллельна плоскости (Q2), то их нормальные векторы коллинеарны, а тогда  = =  = =  . .Расстояние от точки до плоскости. Пусть в пространстве задана точка M0(x0; y0; z0) и плоскость (Q): Ax + By + Cz + D = 0. Расстояние d от точки M0 до плоскости (Q) находится по формуле d =  . .Формула выводится из условия, что d есть модуль проекции вектора  на направление нормального вектора на направление нормального вектора 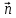 , M1 – произвольная точка плоскости. , M1 – произвольная точка плоскости. 2.2. Уравнения прямой в пространстве Канонические уравнения прямой. Пусть в пространстве задана точка M0(x0; y0; z0) и вектор 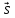 = {m; n; p}. Уравнения прямой (l), которая проходит через точку M0 и которая параллельна вектору = {m; n; p}. Уравнения прямой (l), которая проходит через точку M0 и которая параллельна вектору 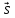 , имеют следующий вид: , имеют следующий вид: = =  = =  . .Эти уравнения называются каноническими и отражают тот факт, что вектор 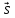 , который называется направляющим вектором прямой, коллинеарен вектору , который называется направляющим вектором прямой, коллинеарен вектору  . Точка M(x; y; z) – произвольная точка прямой (l). . Точка M(x; y; z) – произвольная точка прямой (l). Параметрические уравнения прямой. Запишем канонические уравнения прямой в виде  = =  = =  = t, где t – параметр. Решая каждое из трех записанных таким образом уравнений относительно x, y, z, получим параметрические уравнения прямой = t, где t – параметр. Решая каждое из трех записанных таким образом уравнений относительно x, y, z, получим параметрические уравнения прямойx = x0 + mt; y = y0 + nt; z = z0 + pt. Уравнения прямой, проходящей через две заданные точки. Пусть в пространстве заданы две точки M1(x1; y1; z1) и M2(x2; y2; z2). Уравнения прямой, проходящей через эти точки, имеют вид  = =  = =  . .Эти уравнения получаются из канонических уравнений прямой, если взять за точку на прямой точку M1 а за направляющий вектор - вектор  . .Общие уравнения прямой:  где нормальные векторы плоскостей 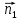 = {A1; B1; C1} и = {A1; B1; C1} и  = {A2; B2; C2} не коллинеарны. Здесь прямая определяется как линия пересечения двух непараллельных плоскостей. = {A2; B2; C2} не коллинеарны. Здесь прямая определяется как линия пересечения двух непараллельных плоскостей.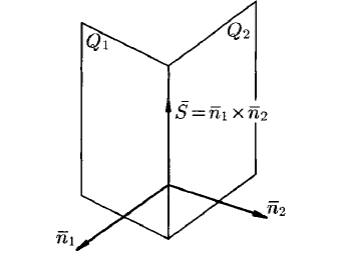 От общих уравнений прямой можно перейти к каноническим уравнениям следующим образом. Координаты точки на прямой получаются из системы уравнений, задав одной из координат произвольное значение (например z = 0).  Пример. Даны вершины треугольника A(2; -3; 4), B(5; -1; -2), C(4; -2; 5). Составить параметрические уравнения его медианы CD. Решение. Изобразим треугольник ABC и его медиану CD на чертеже.  Находим координаты xD, yD, zD точки D по формулам: xD =  = =  = 3,5; yD = = 3,5; yD =  = =  = - 2; zD = = - 2; zD = 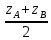 = =  = 1. = 1.Вектор  является направляющим вектором медианы CD. Его координаты находим по формуле: является направляющим вектором медианы CD. Его координаты находим по формуле: = {xD – xC; yD – yC; zD – zC} = {3,5 – 4; -2 +2; 1 – 5} = {-0,5; 0; -4}. = {xD – xC; yD – yC; zD – zC} = {3,5 – 4; -2 +2; 1 – 5} = {-0,5; 0; -4}.Теперь запишем параметрические уравнения медианы CD как прямой, проходящей через точку C(4; -2; 5) и имеющей направляющий вектор  = {-0,5; 0; -4}: = {-0,5; 0; -4}:x = 4 + 0,5t ; y = -2 ; z = 5 + 4t . Расстояние от точки до прямой. Пусть в пространстве задана точка M1(x1; y1; z1) и прямая (l) своими каноническими уравнениями  = =  = =  . Расстояние d от точки M1 до прямой (l) находится по формуле . Расстояние d от точки M1 до прямой (l) находится по формулеd =  , ,где 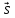 = {m; n; p} – направляющий вектор прямой (l), M0(x0; y0; z0) – точка прямой. Здесь расстояние d находится как высота треугольника, построенного на векторах = {m; n; p} – направляющий вектор прямой (l), M0(x0; y0; z0) – точка прямой. Здесь расстояние d находится как высота треугольника, построенного на векторах  и и 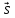 , ,Угол между прямыми. Пусть прямые (l1) и (l2) заданы своими каноническими уравнениями (l1):  = =  = =  , ,(l2):  = =  = =  . .За угол между прямыми (l1) и (l2) принимается угол  , образованный направляющими векторами прямых , образованный направляющими векторами прямых  = {m1; n1; p1} и = {m1; n1; p1} и  = {m2; n2; p2} и его косинус находится по формуле = {m2; n2; p2} и его косинус находится по формуле = =  = =  . .Условие ортогональности двух прямых:  = 0. = 0.Условие параллельности двух прямых:  = =  = =  . .    2.3. Прямая и плоскость в пространстве Угол между прямой и плоскостью. За угол между прямой и плоскостью принимается угол, образованный этой прямой и ее проекцией на рассматриваемую плоскость.  Здесь определяются два угла – острый и тупой. Выбирается один из них. Пусть плоскость (Q) задана общим уравнениемAx + By + Cz + D = 0, а прямая (l) задана каноническими уравнениями  = =  = =  . Синус угла . Синус угла  между прямой (l) и плоскостью (Q) вычисляется по формуле между прямой (l) и плоскостью (Q) вычисляется по формуле = = 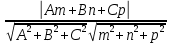 . .Условие параллельности прямой и плоскости:  = 0. = 0.Условие ортогональности прямой и плоскости:  = =  = =  . .  Равенства вида 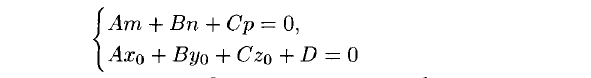 являются условием принадлежности прямой плоскости. Первое равенство отражает тот факт, что прямая параллельна плоскости, а второе – что плоскость проходит через точку на прямой. Замечание. Уравнения прямой на плоскости получаются путем исключения входящих в пространственные уравнения компонент, относящихся к переменной z. Например из канонического уравнения прямой в пространстве получаются уравнения прямой на плоскости вида  = =  . .Пример. Стороны AB и BC параллелограмма заданы уравнениями 2x – y + 5 = 0 и x – 2y + 4 = 0. Диагонали его пересекаются в точке M(1; 4). Найти уравнения двух других сторон параллелограмма. Решение. Изобразим параллелограмм на чертеже.  Находим координаты точки пересечения прямых AB и BC, решая систему уравнений:  Это будет точка B(-2; 1). Теперь найдем координаты точки D, которые обозначим как  и и  . Так как точка M находится на середине отрезка BD, то должны выполняться равенства: . Так как точка M находится на середине отрезка BD, то должны выполняться равенства: , ,  . .Отсюда находим  = 4, = 4,  =7 и D(4; 7). =7 и D(4; 7).Угловые коэффициенты прямых AB и CD совпадают и равны 2. Уравнение прямой CD находим из условия, что ее угловой коэффициент равен 2 и она проходит через точку D(4;7): y – 7 = 2(x – 4), или 2x – y -1 = 0. Аналогично находим уравнение прямой AD: x – 2y +10 = 0. 2.4. Контрольные вопросы 1. Какие Вы знаете уравнения плоскости? 2. Какой смысл имеют коэффициенты A, B, C в уравнении плоскости Ax + By + Cz + D = 0? 3. Плоскость проходит через ось Oz. Какие из коэффициентов A, B, C, D в этом случае равны 0? 4. Какой смысл имеют коэффициенты a, b, c в уравнении плоскости  + +  + +  = 1? = 1?5. Укажите нормирующий множитель для перехода от общего уравнения плоскости к нормальному. 6. Какие Вы знаете уравнения прямой в пространстве? 7. Какой смысл имеют коэффициенты m, n. p в уравнении прямой  = =  = =  ? ?8. Определяет ли прямую система 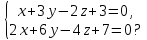 2.5. Расчетное задание Даны координаты четырех точек в пространстве A1, A2, A3, A4 (см. табл.1). Требуется решить следующие задачи: составить уравнение плоскости Q, проходящей через точки A1, A2, A3; составить канонические уравнения прямой, проходящей через точку A4 перпендикулярно плоскости Q; найти координаты точки пересечения такой прямой с плоскостью Q; найти расстояние от точки A4 до плоскости Q; составить уравнение плоскости, проходящей через точку A4 параллельно плоскости Q; составить уравнение плоскости, проходящей через точки A1 и A4 перпендикулярно плоскости Q; найти косинус угла между плоскостью Q и плоскостью, проходящей через точки A1, A3, A4; найти синус угла между прямой A1A4 и плоскостью Q. 2.5. Решение типовых задач Задача 1. Составить уравнение плоскости, проходящей через точки A1(3; -1; 2), A2(4; -1; -1), A3(2; 0; 2). Решение. Воспользуемся уравнением плоскости, проходящей через три заданные точки:  = = 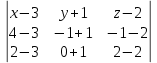 = =  0. 0.Раскрываем определитель третьего порядка: 3(x – 3) + 3(y + 1) + z – 2 = 0, или 3x + 3y + z – 8 = 0. Задача 2. Составить канонические уравнения прямой, проходящей через точку A(-1; 2; 1) перпендикулярно плоскости 3x – 2y + z – 12 = 0. Решение. В качестве направляющего вектора искомой прямой можно взять нормальный вектор заданной плоскости, то есть считаем  = {3; -2; 1}. Тогда канонические уравнения прямой записываются в виде = {3; -2; 1}. Тогда канонические уравнения прямой записываются в виде = =  = =  . .Задача 3. Найти точку пересечения прямой  = =  = =  и плоскости 2x – 6y – z + 1 = 0. и плоскости 2x – 6y – z + 1 = 0.Решение. Запишем уравнения заданной прямой в параметрическом виде: x = 1 + 2t ; y = 2+ 3t ; z = 6 + t . Пусть значение параметра t = ta соответствует точке A(xa; ya; za) пересечения прямой и плоскости. Тогда значение ta находится из уравнения: 2(1 + 2ta) – 6(2+ 3ta) – (6 + ta) +1 = 0. Решая его, получим ta = -1. Координаты точки пересечения A(xa; ya; za) находим из параметрических уравнений прямой при t = -1: xa = 1 + 2(-1) = -1; ya = 2+ 3(-1) = -1; za = 6 - 1 = 5. Значит, точка A(-1; -1; 5) есть точка пересечения прямой и плоскости. Задача 4. Найти расстояние от точки A(-2; -4; 3) до плоскости 2x – y +2z + 3 = 0. Решение. Воспользуемся формулой d =  = =  = 3. = 3.Задача 5. Составить уравнение плоскости, проходящей через точку A(2; -1; 6) параллельно плоскости x + y - 2z + 5 = 0. Решение. В качестве нормального вектора искомой плоскости можно взять нормальный вектор заданной плоскости  = {1; 1; -2}. Искомая плоскость представляется уравнением = {1; 1; -2}. Искомая плоскость представляется уравнением1(x – 2) + 1(y + 1) – 2(z – 6) = 0, или x + y - 2z + 11 = 0. Задача 6. Составить уравнение плоскости, проходящей через точки A1(1; 2; 3) и A2(2; 1; 1) перпендикулярно плоскости 3x + 4y + z - 6 = 0. Решение. Пусть точка M(x; y; z) принадлежит искомой плоскости. Тогда векторы  , ,  и нормальный вектор заданной плоскости и нормальный вектор заданной плоскости 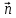 = {3; 4; 1} должны быть комплонарны. Значит выполняется условие = {3; 4; 1} должны быть комплонарны. Значит выполняется условие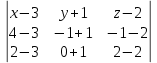 = 0. = 0.Раскрывая определитель третьего порядка, получим искомое уравнение плоскости x - y + z - 2 = 0. Задача 7. Найти косинус угла между плоскостями x - y  + z - 1 = 0 и x + y + z - 1 = 0 и x + y - z + 3 = 0. - z + 3 = 0.Решение. Воспользуемся формулой  = =  = =  = = 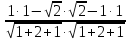 = - = -  . .Задача 8. Найти синус угла между прямой  = =  = =  и плоскостью 6x + 15y - 10z + 31 = 0. и плоскостью 6x + 15y - 10z + 31 = 0.Решение. Воспользуемся формулой  = = 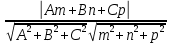 = =  = =  . . |
