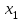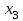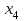Лаба. 1 лаба СЛАУ итер (2). Решение систем линейных алгебраических уравнений (слау) методом итераций Введение Пусть дана система уравнений (10) в обшем систему уравнений (1 0 ) можно представить в виде (1)
 Скачать 154.55 Kb. Скачать 154.55 Kb.
|
|
Решение систем линейных алгебраических уравнений (СЛАУ) методом итераций Введение Пусть дана система уравнений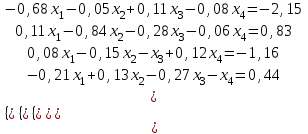 (10) (10)В обшем систему уравнений (10 ) можно представить в виде  (1) (1)Где  - матрица коэффициентов системы уравнений, а - матрица коэффициентов системы уравнений, а 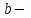 матрица столбец (свободных членов) системы. матрица столбец (свободных членов) системы.Начальную систему уравнений можно привести к виду 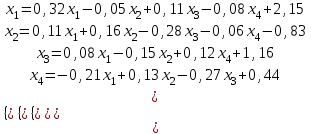 Запишем эту систему в матричном виде  , или обозначая матрицу , или обозначая матрицу  через матрицу через матрицу  приходим к виду приходим к виду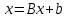 , (2) , (2)здесь  - числовая квадратная матрица - числовая квадратная матрица  -го порядка -го порядка 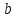 - заданный вектор столбец, - заданный вектор столбец,  . Выбирается произвольный вектор . Выбирается произвольный вектор  (начальное приближение) и строится итерационная последовательность векторов по формуле (начальное приближение) и строится итерационная последовательность векторов по формуле  (3) (3)Введем понятие нормы матрицы (  ). Норма матрицы символически записывается двумя вертикальными черточками в отличии от абсолютной величины. Первая (по максимальному значению) и вторая (по средне квадратичному) нормы матрицы ( ). Норма матрицы символически записывается двумя вертикальными черточками в отличии от абсолютной величины. Первая (по максимальному значению) и вторая (по средне квадратичному) нормы матрицы ( ) вычисляются по формулам ) вычисляются по формулам , ,  . . Если хотя бы одна из норм меньше единицы, то итерационный процесс сходится. Пример пусть определитель матрицы (  ) ) , ,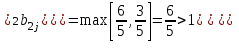 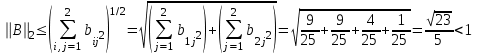 . .Теорема 1. Если норма матрицы   , то система уравнений (2) имеет единственное решение , то система уравнений (2) имеет единственное решение  и последовательные приближения (3) сходятся к решению со скоростью геометрической прогрессии. и последовательные приближения (3) сходятся к решению со скоростью геометрической прогрессии.Доказательство. Пусть  - решение, тогда - решение, тогда  , (4) , (4)тогда для нормы имеем оценку  , ,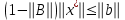 , поскольку , поскольку  , то , то  (5) (5)Из (2) однородной системы при  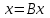  вытекает единственное решение, а следовательно, существование и единственное решение систем (2) и (1) при любом вытекает единственное решение, а следовательно, существование и единственное решение систем (2) и (1) при любом 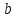 . .Пусть пусть погрешность k- ой итерации  , где , где  -решение системы (2). Вычитая (4)-(3) получаем -решение системы (2). Вычитая (4)-(3) получаем (6) (6)т.е.  , следовательно , следовательно  , где , где  - - 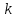 - ая степень матрицы - ая степень матрицы  , , 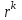 - погрешность - погрешность 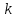 - ой итерации. - ой итерации. , (7) , (7)т.е. норма погрешности 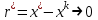 не медленнее геометрической прогрессии со знаменателем не медленнее геометрической прогрессии со знаменателем 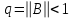 . .Из выражения (7) определяется число необходимых итераций при решении для достижения заданной точности 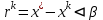  . (8) . (8)Пример. Методом простой итерации решить систему линейных уравнений с точностью до 0,001, предварительно оценив число необходимых для этого шагов 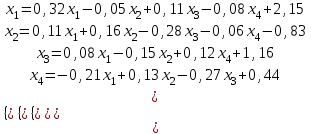 Система уравнений имеет вид 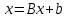 Пусть  - точное решение, - точное решение,  - - -ое приближение -ое приближение  - погрешность нулевого приближения. За погрешность - погрешность нулевого приближения. За погрешность  принимается норма столбца принимается норма столбца  . А первая норма основной матрицы составляет . А первая норма основной матрицы составляет , ,итерационный процесс сходится. 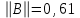 ; ; 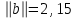 ; ;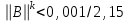 ; ;  При 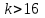 достигается точность достигается точность 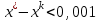 и итерации производятся по формуле и итерации производятся по формуле 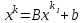 в таблице 1 в таблице 1При 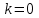 примем примем  , , 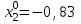 , ,  , , 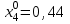 . .А при 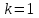 находим находим 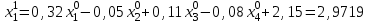 и далее и далееТаблица 1
Сходимость в тысячных долях имеет место уже при  . .Ответ:
Задании по лабораторной работе №1. Решить систему линейных уравнений с точностью до 0,001, предварительно оценив число необходимых для этого шагов итераций. №1.  №2.  №  №4.  №5.  №6.  №7.  №8.  №9.  №10.  №11.  №12.  №13  №14.  №15.  №16.  №17.  №18.  №19.  №20.  №21.  №22.  №23  №24.  №25.  №26.  №27.  №28.  №29.  №30.  |