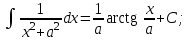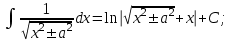Регрессия. Задачи Марк. Операции над векторами
 Скачать 344.43 Kb. Скачать 344.43 Kb.
|
|
Векторы и матрицы в экономике Тема : Операции над векторами. 1) Коллинеарны ли векторы  и и  , разложенные по векторам , разложенные по векторам 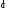 и и 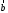 , где , где 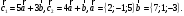 2) Перпендикулярны ли векторы 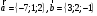 ? ?3) Компланарны ли векторы  ? ?Тема : Использование операции над векторами 1) Найдите сумму векторов  2) Найдите длину векторов  3) Найдите угол между векторами  Первые сведения о матрице, операции над матрицей. Тема : Решение систем линейных алгебраических уравнений с помощью определителя. 1) Методом Крамера найти решение системы линейных алгебраических уравнений 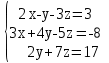 2) Дана система из трех уравнений с тремя неизвестными. Установить, что система уравнений имеет единственное решение и найти его с помощью обратной матрицы  . .3) Методом Крамера найти решение системы линейных алгебраических уравнений 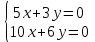 Тема : Решение систем линейных алгебраических уравнений без помощи определителя. Методом Гаусса (или методом исключения неизвестных) найти решение системы линейных алгебраических уравнений 1) 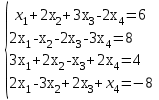 2)  3) 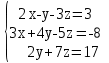 Прямые в пространстве и плоскости Тема : Типы уравнений прямой 1) Составить канонические уравнения прямой, проходящей через точки 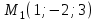 и и 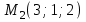 . .2) Найти направляющий вектор прямой 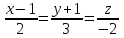 . .3) Найти косинус угла между прямыми  и и 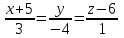 . .Тема : Решение задач на тему уравнений прямой Составить канонические уравнения прямой 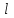 , проходящей через точку , проходящей через точку  параллельно прямой параллельно прямой 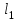 : : 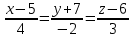 . .Найти угол между прямой 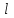 : : 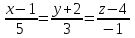 и плоскостью и плоскостью  : : 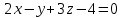 . .Составить уравнение плоскости  , проходящей через точку , проходящей через точку 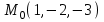 перпендикулярно прямой перпендикулярно прямой 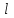 : : 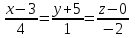 . .Тема : Последовательность. Пределы последовательности. Число В случае, если у числовой последовательности существует предел в виде вещественного числа Кроме того, если все элементы неограниченной последовательности, начиная с некоторого номера, имеют положительный знак, то говорят, что предел такой последовательности равен плюс бесконечности. Если же элементы неограниченной последовательности, начиная с некоторого номера, имеют отрицательный знак, то говорят, что предел такой последовательности равен минус бесконечности. Верхний предел последовательности — это наибольшая из её предельных точек. Нижний предел последовательности — это наименьшая из её предельных точек. Тот факт, что последовательность или Тема : Решение задач на тему пределы последовательности. Общее понятие о функции Тема : Определение предела функции. Определение 1. Число А называется пределом функции f(x) в точке a, если для любого 0 найдётся такое число 0, что из неравенства 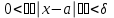 следует неравенство следует неравенство  . .Определение 2. Число А называется правым (левым) пределом функции f(х) в точке а, если для любого 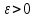 найдётся такое число найдётся такое число 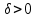 , что из неравенства , что из неравенства  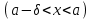 следует неравенство следует неравенство 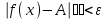 . . Для обозначения правого (левого) предела функции f(x) в точке а используют следующую символику: 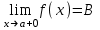  . .Критерий существования предела. Для того, чтобы в точке 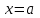 существовал предел функции f(x), необходимо и достаточно, чтобы существовали и были равны между собой оба односторонних предела существовал предел функции f(x), необходимо и достаточно, чтобы существовали и были равны между собой оба односторонних предела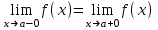 . .Достаточно распространенными в курсе математики являются последовательности, то есть функции 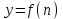 , заданные на множестве натуральных чисел N. Чтобы подчеркнуть, что аргумент такой функции принимает только значения из множества натуральных чисел, его обозначают не х, а n. Для последовательностей f(n) достаточно часто возникает необходимость найти ее предел при неограниченном возрастании аргумента n (при , заданные на множестве натуральных чисел N. Чтобы подчеркнуть, что аргумент такой функции принимает только значения из множества натуральных чисел, его обозначают не х, а n. Для последовательностей f(n) достаточно часто возникает необходимость найти ее предел при неограниченном возрастании аргумента n (при  ). ).Тема : Решение задач на тему пределы функции 1) 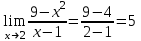 2) 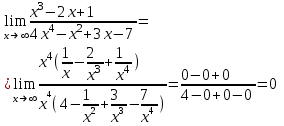 3)  Производная и дифференциал Тема : Определение производной функции. Определение производной Пусть задана функция f(x) на интервале (a,b). Зафиксируем точку x внутри (a,b) и придадим x приращение ∆x, MP секущая, приращение функции ∆y = f(x+∆x)-f(x). Рассмотрим отношение 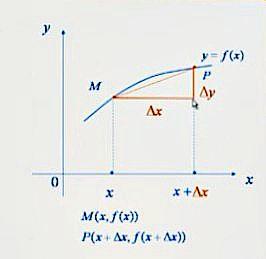 Определение. Производной называется предел отношения приращения функции к приращению аргумента , когда приращение аргумента стремится к нулю: Существует несколько способов обозначения производной, самые важные это Пример нахождения Тема : Физическая значение производной функций Пусть прямолинейное движение материальной точки задано законом S = S(t). Путь, который проследует точка за время ∆t равен ∆S = S(t+∆t)-S(t). Средняя скорость есть Пример. Пусть дан закон движения материальной точки Функции многих переменных Тема : Способы передачи функции многих переменных Функция, определенная на некотором множестве 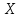 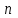 -мерноговекторного пространства, называется функцией -мерноговекторного пространства, называется функцией 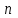 аргументов: аргументов: , ,где  — координаты точки — координаты точки  данного множества. данного множества.Переменная величина 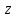 называется функцией двух переменных величин называется функцией двух переменных величин 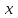 и и 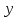 на множестве на множестве 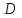 , если каждой паре значений , если каждой паре значений 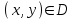 соответствует единственное значение величины соответствует единственное значение величины 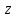 . .Символически функция двух переменных обозначается так: 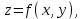 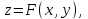 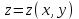 и т.д. и т.д.Переменные 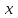 и и 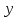 называются независимыми переменными или аргументами функции, а множество называются независимыми переменными или аргументами функции, а множество 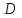 — областью определения функции. — областью определения функции.Например,  — функция двух переменных. — функция двух переменных.Тема : Решение задач на тему функции многих переменных 1) Предприятие имеет участок производства и склад. Склад обеспечивает ритмичность работы – если продукцию не удаётся сбыть сразу, то её можно хранить на складе. Наличие склада приводит к издержкам хранения. В простейшем случае эти издержки за единицу времени пропорциональны числу изделий  , хранящихся на складе, т.е. они равны , хранящихся на складе, т.е. они равны 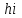 , где , где  — издержки хранения одного изделия в течение одной единицы времени. Издержки производства за единицу времени в простейшем случае также равны — издержки хранения одного изделия в течение одной единицы времени. Издержки производства за единицу времени в простейшем случае также равны  , где , где 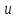 — число произведённых за единицу времени изделий, а — число произведённых за единицу времени изделий, а 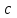 — себестоимость производства одного изделия. К этим издержкам добавляются ещё накладные расходы — себестоимость производства одного изделия. К этим издержкам добавляются ещё накладные расходы 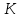 — это расходы в единицу времени на поддержание рабочего состояния предприятия, они практически не зависят от интенсивности работы и включают расходы на охрану, дежурных рабочих и т.д. Все издержки — это расходы в единицу времени на поддержание рабочего состояния предприятия, они практически не зависят от интенсивности работы и включают расходы на охрану, дежурных рабочих и т.д. Все издержки 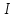 за единицу времени получаются равными за единицу времени получаются равными 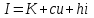 . .2) Пусть 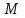 — это общее количество денег, — это общее количество денег,  — скорость их обращения (сколько раз каждый рубль, доллар участвуют в расчётах в среднем за год), — скорость их обращения (сколько раз каждый рубль, доллар участвуют в расчётах в среднем за год), 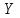 — национальный продукт или доход (национальный продукт – это все готовые товары и услуги, произведённые в экономической системе в стоимостном выражении; национальный доход – это все выплаты, получаемые домашними хозяйствами: заработная плата, рента, прибыль; национальный продукт и национальный доход численно равны). Пусть — национальный продукт или доход (национальный продукт – это все готовые товары и услуги, произведённые в экономической системе в стоимостном выражении; национальный доход – это все выплаты, получаемые домашними хозяйствами: заработная плата, рента, прибыль; национальный продукт и национальный доход численно равны). Пусть  — это уровень цен (среднее взвешенное значение цен готовых товаров и услуг, выраженное относительно базового показателя, принятого за единицу). Связывая все эти величины, получим уравнение денежного обращения — основное уравнение классической количественной теории денег, так называемое уравнение обмена Фишера: — это уровень цен (среднее взвешенное значение цен готовых товаров и услуг, выраженное относительно базового показателя, принятого за единицу). Связывая все эти величины, получим уравнение денежного обращения — основное уравнение классической количественной теории денег, так называемое уравнение обмена Фишера: 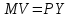 .Любая из переменных .Любая из переменных 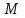 , ,  , ,  , , 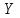 может рассматриваться как функция трёх остальных. может рассматриваться как функция трёх остальных.Например,  и видим, что если государство увеличит число денег и видим, что если государство увеличит число денег 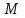 в обращении в 2 раза (т.е. просто деньги напечатают), то и цены возрастут в два раза (при условии, что остальные величины, т.е. в обращении в 2 раза (т.е. просто деньги напечатают), то и цены возрастут в два раза (при условии, что остальные величины, т.е.  , , 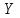 , останутся неизменными). Такие действия чаще всего и есть причина инфляции. , останутся неизменными). Такие действия чаще всего и есть причина инфляции.Частные производные Тема : Частные производные второго высшего порядка Частными производными второго порядка от функции 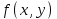 называются соответствующие частные производные от ее частных производных первого порядка, если они существуют. называются соответствующие частные производные от ее частных производных первого порядка, если они существуют. Для функции 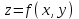 по определению имеем по определению имеем  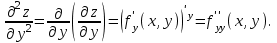   Частные производные второго порядка, взятые по различным переменным называются смешанными. Т 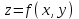 и ее смешанные производные и ее смешанные производные  , ,  определены в некоторой окрестности точки определены в некоторой окрестности точки  и непрерывны в этой точке, то и непрерывны в этой точке, то 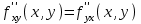 . .Дифференцируя частные производные второго порядка как по х, так и по у, получим частные производные третьего порядка. Тема : Частные производные высшего порядка 1)Дана функция 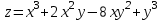 . Найти ее частные производные второго порядка. . Найти ее частные производные второго порядка.Н  : :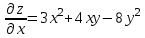 , , 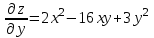 , ,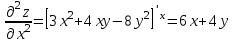 , ,  , , , ,  . .2)Найти частные производные второго порядка функции  . .Последовательно находим  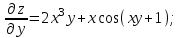 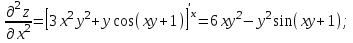  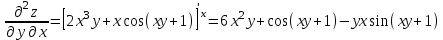 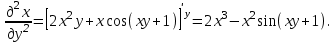 Задачи оптимизации в экономике Тема : Экстремум функции и его определение. Точка  называется точкой максимума (maximum) функции называется точкой максимума (maximum) функции 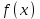 , если значение функции в этой точке больше её значений во всех точках некоторого интервала, содержащего точку , если значение функции в этой точке больше её значений во всех точках некоторого интервала, содержащего точку  , т.е. , т.е. 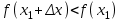 для любого для любого 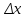 ( (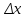 — мало по величине). — мало по величине).Точка 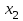 называется точкой минимума (minimum) функции называется точкой минимума (minimum) функции 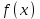 , если значение функции в этой точке меньше её значений во всех точках некоторого интервала, содержащего точку , если значение функции в этой точке меньше её значений во всех точках некоторого интервала, содержащего точку 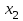 , т.е. , т.е.  . .Точки, в которых функция достигает максимума или минимума, называются точками экстремума функции, а значения функции в этих точках называют экстремальными.  Функция, заданная кривой на рисунке выше, в точках  и и  достигает максимума, в точках достигает максимума, в точках 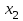 и и 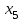 — минимума, в точке — минимума, в точке 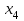 — экстремума нет. Очевидно, что функция имеет производную, равную нулю в критических точках. Касательная к кривой в этих точках параллельна оси — экстремума нет. Очевидно, что функция имеет производную, равную нулю в критических точках. Касательная к кривой в этих точках параллельна оси  . .Тема : Экстремум функции и его нахождение. 1) Найдите экстремумы функции 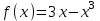 . .2)Найдите экстремумы функции 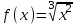 . .3)С помощью производной первого порядка найдите интервалы монотонности и точки экстремума функции 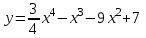 . .Определенный и неопределенный интеграл Тема : Простое правило интегрирования. Таблица основных интегралов
Тема : Интегрирование по частям. 1) 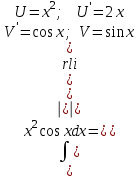 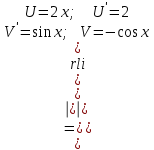 {для нахождения интеграла применим формулу (6)} 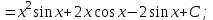 2)  {второе слагаемое вычислим с помощью замены, применив формулу (2)} 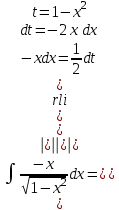 в итоге получаем 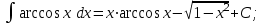 Тема : Дифференциальные уравнения 1го порядка Определение 1. Дифференциальным уравнением первого порядка называется соотношение, связывающее независимую переменную, искомую функцию и ее производную:  (1) (1)Обычно мы будем иметь дело с уравнениями, которые можно разрешить относительно производной   (2) (2)Если в (2) положить  , то уравнение (2) можно записать в симметричной форме: , то уравнение (2) можно записать в симметричной форме: 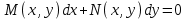 (3) (3)Здесь переменные x и y равноправны. Иногда бывает выгодно рассматривать х как функцию y. В этом случае часто применяют форму записи (3). Пример. 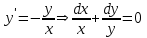 Тема : Дифференциальные уравнения 2го порядка Определение 1. Обыкновенным дифференциальным уравнением n–ого порядка называется соотношение вида:  (1), (1),где 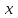 – независимая переменная; – независимая переменная; 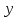 – искомая функция переменной; – искомая функция переменной; – производные искомой функции; – производные искомой функции;  – известная функция своих аргументов. – известная функция своих аргументов.Считается, что производная 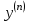 на самом деле входит в выражение (1), а величины на самом деле входит в выражение (1), а величины  могут и не входить в него. могут и не входить в него.Определение 2. Порядком дифференциального уравнения, n, называется наивысший порядок производной, входящей в это уравнение. Пример. 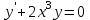 – уравнение первого порядка; – уравнение первого порядка; – уравнение второго порядка; – уравнение второго порядка;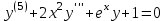 – уравнение пятого порядка. – уравнение пятого порядка.Определение 3. Всякая функция  , которая, будучи подставленная вместо y в выражение (1), обращает это выражение в тождество, называется решением дифференциального уравнения (1). , которая, будучи подставленная вместо y в выражение (1), обращает это выражение в тождество, называется решением дифференциального уравнения (1).Если  – решение, то по определению – решение, то по определению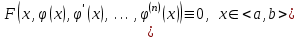 (2) (2)Пример. 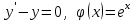 – решение, так как – решение, так как 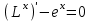 У рассматриваемого уравнения есть еще такое решение:  где С – произвольная постоянная. Это значит, что это уравнение имеет бесчисленное множество решений, зависящих от одного параметра (С). Можно показать, что уравнение n–ого порядка имеет семейство решений, зависящих от произвольных независимых друг от друга постоянных. Пример. Уравнение  имеет решение: имеет решение: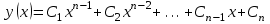 . .Тема : Расчет вероятности Задача 1. В ящике 5 апельсинов и 4 яблока. Наудачу выбираются 3 фрукта. Какова вероятность, что все три фрукта – апельсины? Решение. Элементарными исходами здесь являются наборы, включающие 3 фрукта. Поскольку порядок фруктов безразличен, будем считать их выбор неупорядоченным (и бесповторным). Общее число элементарных исходов  равно числу способов выбрать 3 фрукта из 9, т.е. числу сочетаний равно числу способов выбрать 3 фрукта из 9, т.е. числу сочетаний  . Число благоприятствующих исходов . Число благоприятствующих исходов 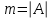 равно числу способов выбора 3 апельсинов из имеющихся 5, т.е. равно числу способов выбора 3 апельсинов из имеющихся 5, т.е.  . Тогда искомая вероятность . Тогда искомая вероятность . .Задача 2. Преподаватель предлагает каждому из трех студентов задумать любое число от 1 до 10. Считая, что выбор каждым из студентов любого числа из заданных равновозможен, найти вероятность того, что у кого-то из них задуманные числа совпадут. Решение. Вначале подсчитаем общее количество исходов. Первый из студентов выбирает одно из 10 чисел и имеет n1=10 возможностей, второй тоже имеет n2=10 возможностей, наконец, третий также имеет n3=10 возможностей. В силу правила умножения общее число способов равно: n= n1n2n3=103 = 1000, т.е. все пространство содержит 1000 элементарных исходов. Для вычисления вероятности события A удобно перейти к противоположному событию, т.е. подсчитать количество тех случаев, когда все три студента задумывают разные числа. Первый из них по-прежнему имеет m1=10 способов выбора числа. Второй студент имеет теперь лишь m2=9 возможностей, поскольку ему приходится заботиться о том, чтобы его число не совпало с задуманным числом первого студента. Третий студент еще более ограничен в выборе — у него всего m3=8 возможностей. Поэтому общее число комбинаций задуманных чисел, в которых нет совпадений, равно m=1098=720. Случаев, в которых есть совпадения, остается 280. Следовательно, искомая вероятность равна Р=280/1000= 0,28. Случайные величины Тема : Характеристики случайных величин Математическое ожидание дискретной случайной величины Пусть дан ряд распределения дискретной случайной величины с конечным числом значений.
Определение. Математическим ожиданием дискретной случайной величины X называется величина MX, равная: 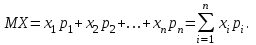 (1) (1)Пусть дискретная случайная величина имеет бесконечное число возможных значений. Определение. Математическим ожиданием дискретной случайной величины X называется величина MX, равная: 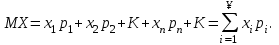 (2) (2)при условии, что абсолютно сходится ряд (2). 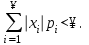 Математическое ожидание есть среднее значение случайной величины. Тема : Дисперсия и ее свойства Найдите дисперсию 1)
2)
Тема : Нахождение дисперсий Найдите дисперсию 1)
2)
|

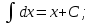

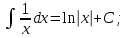
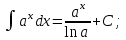 4а
4а