05.12.20. Лекция 1Понятие отношения. Понятие отношения. Свойства отношений. Отношение эквивалентности и порядка
 Скачать 102.72 Kb. Скачать 102.72 Kb.
|
|
Тема: «Понятие отношения. Свойства отношений. Отношение эквивалентности и порядка» ЦЕЛЬ: образовательная: изучить понятие бинарного отношения, его свойства, отношения эквивалентности и порядка развивающая: научиться решать задачи по теме «Отношения» воспитательная: воспитывать ответственность за свои действия и поступки. ВИД ЗАНЯТИЯ: лекция. ОБОРУДОВАНИЕ: компьютер ЛИТЕРАТУРА: ЛИТЕРАТУРА: Алимов Ш.А. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10-11 классы: учеб. для общеобразовательных организаций: базовый и углубленный уровень / Ш.А.Алимов, Ю.М. Колягин и др. – М.: Просвещение, 2016. Анастасян Л.С. Геометрия, 10 11 учеб. для общеобразоват. учреждений/ [Л.С. Анастасян, В.Ф. Бутузов, С.Б. Кадомец и др.]/ – 15-е изд. – М.: Просвещение, 2009. – 256с. Башмаков М.И. Математика: учебник для учреждений нач. и сред. проф. образования/М.И. Башмаков. –М.: Издательский центр Академия», 2010.– 256с. Пехлецкий И.Д. Математика: учебник для студ. образов. учреждений сред. проф. Образования / И.Д. Пехлецкий – 6-е изд., стер. М.: Издательский центр Академия, 2010. – 304с. Стойлова Л. П., Пышкало А. М. Основы начального курса математики: Учеб. пособие для учащихся пед. уч-щ по спец. № 2001 «Преподавание в нач. классах общеобразоват. шк.» – М.: Просвещение, 1988.– 320 с.: ил. Стойлова Л.П. Математика: Учебник для студ. высш. пед. учеб. заведений.- М.: Издательский центр «Академия», 1999.- 424 с. ХОД ЗАНЯТИЯ 1. Вступительная часть. 1.1. Организация студентов. 1.2. Мотивация учебной деятельности. 2. Изложение материала лекции (план и текст лекции) План Понятие отношения между элементами одного множества. Способы задания отношений. Свойства бинарных отношений. Отношение эквивалентности. Отношение порядка. 1. Понятие отношения между элементами одного множества В математике изучают не только сами объекты (числа, фигуры, величины), но и связи, отношения между ними. Отношения многообразны. Между понятиями – это отношения рода и вида, части и целого; между предложениями – отношения следования и равносильности; между числами – «больше», «меньше», «равно», «больше на…», «следует» и др. Изучение отношений между объектами важно для познания как самих объектов, так и для познания реального мира в целом. В нашем курсе мы будем рассматривать в основном бинарные отношения, т.е отношения между двумя элементами. Чтобы определить общее понятие отношения на множестве, рассмотрим сначала конкретный пример. Пусть на множестве Х = 2, 4, 6, 8 задано отношение «меньше». Это означает, что для любых двух чисел из множества Х можно сказать, какое из них меньше: 2 4, 2 6, 2 8, 4 6, 4 8, 6 8. Но все эти пары есть элементы декартова произведения ХХ, поэтому об отношении «меньше», заданном на множестве Х, можно сказать, что оно является подмножеством множества ХХ. Определение. Отношением между элементами множества Х или отношением на множестве Х называется всякое подмножество декартова произведения ХХ. Так как в дальнейшем мы будем рассматривать только бинарные отношения, то определимся, на множестве Х мы их будем определять следующим образом: Определение. Бинарным отношением на множестве Х называется всякое подмножество декартова произведения ХХ. Условимся отношения обозначать буквами R, S, T, P и др. Если R – отношения на множестве Х, то, согласно определению, R ХХ. С другой стороны, если задано некоторое подмножество множества ХХ , то оно определяет на множестве Х некоторое отношение R. Замечание. Утверждение о том, что элементы х и у находятся в отношении R, можно записать так: (х,у) R или х R у. Последняя запись читается : “Элемент х находится в отношении R с элементом у”. 2. Способы задания отношений По определению отношения R между элементами множества Х есть всякое подмножество декартова произведения Х Х, т.е. множество, элементами которого являются упорядоченные пары. Поэтому способы задания отношений, по существу, такие же, как и способы задания множеств. Отношение R на множестве Х можно задать, перечислив все пары элементов, взятых из множества Х и связанных этим отношением. Формы записи при этом могут быть различными. Например, некоторое отношение R на множестве Х = 4, 5, 6, 7, 9можно задать, записав множество пар: (5,4),(6,4),(6,5),(7,4),(7,5),(7,6),(9, 4),(9,5),(9,6),(9,7).То же отношение можно задать при помощи графа. Отношения на конечном множестве Х можно представлять наглядно, при помощи особых чертежей, состоящих из точек, соединенных стрелками. Такие чертежи называют графами. Построим граф отношения «меньше», заданного на множестве Х = 2, 4, 6, 8. Для этого элементы множества Х изобразим точками (их называют вершинами графа), а отношение «меньше» – стрелкой.  2• • 4 8 6 Пример На том же множестве Х можно рассмотреть другое отношение – «кратно». Граф этого отношения будет в каждой вершине иметь петлю (стрелку, начало и конец которой совпадают), так как каждое число кратно самому себе.         2 4 2 4    8 6 8 6Чаще отношение R на множестве Х задают, указав характеристическое свойство всех пар элементов, находящихся в отношении R. Это свойство задается при помощи предложения с двумя переменными. Пример. Пусть заданы рассмотренные выше отношения «меньше» и «кратно», причем использована краткая форма предложений«число х меньше числа у» и «число х кратно числу у». Некоторые такие предложения можно записать используя символы. Например, отношения «меньше» и «кратно» можно было записать в таком виде: «х у», «х  у». Отношение «х больше у на 3» можно записать в виде равенства х = у + 3 (или х – у = 3). Отношение между прямыми плоскости задают, используя символы: х // у, х у. у». Отношение «х больше у на 3» можно записать в виде равенства х = у + 3 (или х – у = 3). Отношение между прямыми плоскости задают, используя символы: х // у, х у.Для отношения R, заданного на множестве Х, всегда можно задать отношение R -1 , ему обратное. Например, если R – отношение “х меньше у”, то обратным ему будет отношение “ у меньше х”. Понятием отношения, обратного данному, часто пользуются при начальном обучении математике. Например, чтобы предупредить ошибку в выборе действия, с помощью которого решается задача: «У Пети 7 карандашей, что на 2 меньше, чем у Бори. Сколько карандашей у Бори?» – ее переформулируют: «У Пети 7 карандашей, а у Бори на 2 больше. Сколько карандашей у Бори?». Видим, что переформулировка свелась к замене отношения «меньше на 2» обратным ему отношением «больше на 2». 3. Свойства бинарных отношений Мы установили, что бинарное отношение на множестве Х представляет собой множество упорядоченных пар элементов, принадлежащих декартову произведению Х. Это математическая сущность всякого отношения. Но, как и любые другие понятия, отношения обладают свойствами. Их удалось выделить, изучая различные конкретные отношения. Свойств достаточно много, в нашем курсе мы будем изучать только некоторые. Рассмотрим на множестве отрезков, представленных на рисунке, отношения перпендикулярности, равенства и «длиннее».  Построим графы этих отношений и будем их сравнивать.  Граф отношения перпендикулярности   Определение. Отношение R на множестве Х называется рефлексивным, если о каждом элементе множества Х можно сказать, что он находится в отношении R с самим собой. Используя символы, это отношение можно записать в таком виде: R рефлексивно на Х х R х для любого х Х. Замечание: Если отношение R рефлексивно на множестве Х, то в каждой вершине графа данного отношения имеется петля. Справедливо и обратное утверждение: граф, каждая вершина которого имеет петлю, задает отношения, обладающие свойством рефлексивности. Примеры рефлексивных отношений: отношение «кратно» на множестве натуральных чисел (каждое натуральное число кратно самому себе); отношение подобия треугольников (каждый треугольник подобен самому себе). Существуют отношения, которые свойством рефлексивности не обладают. Примеры отношений, которые свойством рефлексивности не обладают: отношение перпендикулярности на множестве отрезков (нет ни одного отрезка, о котором можно сказать, что он перпендикулярен самому себе); отношение «длиннее» для отрезков. Обратим внимание на графы отношений перпендикулярности и равенства отрезков. Они «похожи» тем, что если есть одна стрелка, соединяющая пару элементов, то обязательно есть и другая, соединяющая те же элементы, но идущая в противоположном направлении. Эта особенность графа отражает те свойства, которыми обладают отношения параллельности и равенства отрезков: если один отрезок перпендикулярен другому отрезку, то этот «другой» перпендикулярен первому; если один отрезок равен другому отрезку, то этот «другой» равен первому. Про отношения перпендикулярности и равенства отрезков говорят, что они обладают свойством симметричности или просто симметричны. Определение. Отношение R на множестве Х называется симметричным, если выполняется условие: из того, что элемент х находится в отношении R с элементом у, следует, что и элемент у находится в отношении R с элементом х. Используя символы, это отношение можно записать в таком виде: R симметрично на Х ( х R х у Rх). Замечание. Граф симметричного отношения обладает особенностью: вместе с каждой стрелкой, идущей от х к у, граф содержит и стрелку, идущую от у к х. Справедливо и обратное утверждение. Граф, содержащий вместе с каждой стрелкой, идущей от х к у, и стрелку, идущую от у к х, является графом симметричного отношения. Примеры симметричных отношений: отношение параллельности на множестве прямых (если прямая х параллельна прямой у, то прямая у параллельна прямой х); отношение подобия треугольников (если треугольник F подобен треугольнику Р, то треугольник Р подобен треугольнику F). отношение перпендикулярности на множестве отрезков (если один отрезок перпендикулярен другому отрезку, то этот «другой» перпендикулярен первому); отношение «длиннее» для отрезков (если один отрезок равен другому отрезку, то этот «другой» равен первому). Пример Рассмотрим отношение «длиннее» на множестве отрезков, которое свойством симметричности не обладает. Действительно, если отрезок х длиннее отрезка у, то отрезок у не может быть длиннее отрезка х. Про отношения «длиннее» говорят, что оно обладает свойством антисимметричности или просто антисимметрично. Определение. Отношение R на множестве Х называется антисимметричным, если для различных элементов х и у из множества Х выполнено условие: из того, что элемент отношении R с элементом х не находится. Используя символы, это отношение можно записать в таком виде: R антисимметрично на Х ( х R у  ху ху  ). ).Замечание. Граф антисимметричного отношения обладает особенностью: если вершины графа соединены стрелкой, то эта стрелка только одна. Справедливо и обратное утверждение: граф, вершины которого соединены только одной стрелкой, есть граф антисимметричного отношения. Примеры антисимметричных отношений: отношение «длиннее» на множестве отрезков; отношение «больше» для чисел (если х больше у, то у не может быть больше х); отношение «больше на 2» для чисел (если х больше у на 2, то у не может быть больше на 2 числа х). Пример Рассмотрим отношение «быть сестрой» на множестве детей одной семьи, которое не обладает ни свойством симметричности, ни свойством антисимметричности. Пусть в семье трое детей: Катя, Маша, и Толя. Тогда граф отношения» быть сестрой» будет таким:  Он показывает, что данное отношение не обладает ни свойством симметричности, ни свойством антисимметричности. Обратим внимание еще на одну особенность графа отношения «длиннее». На нем можно заметить: если стрелки проведены от е к а и от а к с, то есть стрелка от е к с; если стрелки проведены от е к в и от в к с, то есть стрелка и от е к с и т.д. Эта особенность графа отражает важное свойство отношения «длиннее»: если первый отрезок длиннее второго, а второй – длиннее третьего, то первый – длиннее третьего. Говорят, что это отношение обладает свойством транзитивности или просто транзитивно. Определение. Отношение R на множестве Х называется транзитивным, если выполняется условие: из того, что элемент х находится в отношении R с элементом у находится в отношении R с элементом z, следует, что и элемент х в отношении R с элементом z. Используя символы, это отношение можно записать в таком виде: R транзитивно на Х ( х R у  у R zх R z). у R zх R z).Замечание. Граф транзитивного отношения с каждой парой стрелок, идущих от х к у и у к z, содержит стрелку, идущую от х к z. Справедливо и обратное утверждение. Примеры транзитивных отношений: отношение «длиннее» на множестве отрезков; отношение равенства (если отрезок х равен отрезку у и отрезок у равен отрезку z, то отрезок х равен отрезку z. Существуют отношения, которые свойством транзитивности не обладают. Таким отношением является, например, отношение перпендикулярности: если отрезок а перпендикулярен отрезку d, а отрезок d перпендикулярен отрезку b, то отрезки а и b не перпендикулярны. Рассмотрим еще одно свойство отношений, которое называют свойством связности, а отношение, обладающее им, называют связанным. Определение. Отношение R на множестве Х называется связанным, если для любых элементов х и у из множества Х выполнено условие: из того, что х и у различны, следует, что либо х находится в отношении R с элементом у, либо элемент у находится в отношении R с элементом х. Используя символы, это отношение можно записать в таком виде: R связано на множестве Х ( ху х R у у R х). Свойством связности обладают отношения «больше» для натуральных чисел: для различных чисел х и у можно утверждать, что х у, либо у х. Замечание. На графе связного отношения любые две вершины соединены стрелкой. Справедливо и обратное утверждение. Существуют отношения, которые свойством связности не обладают. Таким отношением, например, является отношение делимости на множестве натуральных чисел: можно назвать такие числа х и у, что ни число х не является делителем числа у, ни число у не является делителем числа х. Выделенные свойства позволяют анализировать различные отношения с общих позиций – наличия (или отсутствия) у них тех или иных свойств. Так, если суммировать все сказанное об отношении равенства, заданного на множестве отрезков, то получится, что оно рефлексивно, симметрично и транзитивно. Отношение «длиннее» на том же множестве отрезков антисимметрично и транзитивно, а отношение перпендикулярности – симметрично, но оно не обладает свойствами рефлексивности и транзитивности. Все эти отношения на заданном множестве отрезков связанными не являются. Пример Сформулировать свойства отношения «больше в 2 раза», заданного на множестве натуральных чисел. Решение. «Больше в 2 раза» - это краткая запись отношения «число х больше числа у в 2 раза». Это отношение антисимметрично, так как выполняется условие: из того, что число х больше числа у в 2 раза, следует, что число у не больше числа х в 2 раза. Данное отношение не обладает свойством рефлексивности, потому что ни про одно число нельзя сказать, что оно больше самого себя в 2 раза. Заданное отношение не транзитивно, так как из того, что число х больше числа у в 2 раза, а число у больше числа z в 2 раза, следует, что число х не может быть больше числа z в 2 раза. Это отношение на множестве натуральных чисел свойством связности не обладает, так как существуют пары таких чисел х и у, что ни число х не больше числа у в два раза, ни число у не больше х в 2 раза. Например, это числа 7 и 3, 5 и 8 и др. Отношение эквивалентности и порядка Рассмотрим на множестве дробей Х=  отношение равенства. Это отношение: отношение равенства. Это отношение:рефлексивно, так как всякая дробь равна сама себе; симметрично, так как из того, что дробь  равна дроби равна дроби 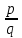 и дробь и дробь 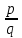 равна дроби равна дроби 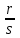 , следует, что дробь , следует, что дробь  равна дроби равна дроби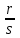 . .Про отношение равенства дробей говорят, что оно является отношением эквивалентности. Определение. Отношение R на множестве Х называется отношение эквивалентности, если оно одновременно обладает свойствами рефлексивности, симметричности и транзитивности. Примерами отношений эквивалентности могут служить отношения равенства геометрических фигур, отношение параллельности прямых (при условии, что совпадающие прямые считаются параллельными). Почему в математике выделили этот вид отношений? Рассмотрим отношение равенства дробей, заданное на множестве Х=   Видим, что множество разбилось на три подмножества:  , , , , . Эти подмножества не пересекаются, а их объединение совпадает с множеством Х, т.е. имеет разбиение множества Х на классы. Это не случайно. . Эти подмножества не пересекаются, а их объединение совпадает с множеством Х, т.е. имеет разбиение множества Х на классы. Это не случайно.Замечание. Если на множестве Х задано отношение эквивалентности, то оно порождает разбиение этого множества на попарно не непересекающиеся подмножества (классы эквивалентности). Так, мы установили, что отношению равенства на множестве дробей  соответствует разбиению этого множества на классы эквивалентности, каждый из которых состоит из равных между собой дробей. соответствует разбиению этого множества на классы эквивалентности, каждый из которых состоит из равных между собой дробей.Замечание. Верно и обратное утверждение: если какое – либо отношение, заданное на множестве Х, порождает разбиение этого множества на классы, то оно является отношением эквивалентности. Пример Рассмотрим на множестве Х = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 отношение «иметь один и тот же остаток при делении на 3». Оно порождает разбиение множества Х на классы: в один попадут все числа, при делении которых на 3 получается в остатке 0 (это числа 3, 6, 9), во второй – числа, при делении которых на 3 в остатке получается 1(это числа 1, 4, 7, 10), и в третий – все числа, при делении которых на 3 в остатке получается 2 (это числа 2, 5, 8). Действительно, полученные подмножества не пересекаются и их объединение совпадает с множеством Х. Следовательно, отношение «иметь один и тот же остаток при делении на 3», заданное на множестве Х, является отношением эквивалентности. Утверждения о взаимосвязи отношения эквивалентности и разбиения на классы мы принимаем без доказательства. Если отношение эквивалентности имеет название, то соответствующее название дается и классам. Например, если на множестве отрезков задать отношение равенства (оно является отношением эквивалентности), то множество отрезков разобьется на классы равных отрезков. Множество треугольников отношением подобия разбивается на классы подобных треугольников. Принцип разбиения множества на классы при помощи некоторого отношения эквивалентности является важным принципом математики. Во-первых, эквивалентный – это значит равносильный, взаимозаменяемый. Поэтому элементы одного класса эквивалентности взаимозаменяемые. Так, дроби, оказавшиеся в одном классе эквивалентности  , неразличимы с точки зрения отношения равносильности, и дробь , неразличимы с точки зрения отношения равносильности, и дробь  может быть заменена другой, например может быть заменена другой, например  . И эта замена не изменит результата вычислений. . И эта замена не изменит результата вычислений.Во–вторых, поскольку в классе эквивалентности оказываются элементы, неразличимые с точки зрения некоторого отношения, то считают, что класс эквивалентности определяется любым своим представителем, т.е. произвольным элементом этого класса. Так, любой класс равных дробей можно задать, указав любую дробь, принадлежащую этому классу. Определение класса эквивалентности по одному представителю позволяет вместо всех элементов множества изучать совокупность отдельных представителей из классов эквивалентности. Например, отношение эквивалентности «иметь одинаковое число вершин», заданное на множестве многоугольников, порождает разбиение этого множества на классы треугольников, четырехугольников, пятиугольников и т.д. Свойства, присущие некоторому классу, рассматриваются на одном его представителе. В-третьих, разбиение множества на классы с помощью отношения эквивалентности используется для введения новых понятий. Например, понятие «пучок прямых» можно определить как то общее. Что имеют параллельные между собой прямые. Вообще любое понятие, которым оперирует человек, представляет собой некоторый класс эквивалентности. «Стол», «дом», «книга» – все эти понятия являются обобщенными представлениями о множестве конкретных предметов, имеющих одинаковое назначение. Другим важным видом отношений являются отношения порядка. Определение. Отношение R на множестве Х называется отношение порядка, если оно одновременно обладает свойствами антисимметричности и транзитивности. Примеры отношений порядка: отношение «меньше» на множестве натуральных чисел; отношение «короче» на множестве отрезков. Если отношение порядка обладает еще свойством связности, то говорят, что оно является отношением линейного порядка. Например, отношение «меньше» на множестве натуральных чисел является отношением линейного порядка, так как обладает свойствами антисимметричности, транзитивности и связности. Определение. Множество Х называется упорядоченным, если на нем задано отношение порядка. Так, множество N натуральных чисел можно упорядочить, если задать на нем отношение «меньше». Если отношение порядка, заданное на множестве Х, обладает свойством связности, то говорят, что оно линейно упорядочивает множество Х. Например, множество натуральных чисел можно упорядочить и с помощью отношения «меньше», и помощью отношения «кратно» – оба они являются отношениями порядка. Но отношение «меньше», в отличие от отношения «кратно», обладает еще и свойством связности. Значит, отношение «меньше» упорядочивает множество натуральных чисел линейно. Не следует думать, что все отношения делятся на отношения эквивалентности и отношения порядка. Существует огромное количество отношений, не являющихся ни отношениями эквивалентности, ни отношениями порядка. Решить задачи Приведите примеры отношений, существующих между: а) натуральными числами; б) прямыми на плоскости; в) треугольниками; г) множествами. На множестве Х=0, 3, 6, 9, 12, 15, 18 задано отношение R. Перечислите пары чисел, связанных этим отношением и постройте его граф, если: а) R – « х больше у в 3 раза»; б) R – « х больше у на 3». 3. Заключительная часть. Домашнее задание: Решить задачи Отношение « х у» рассматривается на множестве Х. Каким будет его график на координатной плоскости, если: а) Х = 2,4,6,8; б) Х – множество натуральных чисел; в) Х – множество действительных чисел? На множестве отрезков задано отношение Р: «отрезок х длиннее отрезка у». Постройте граф этого отношения и задайте различными способами отношение, обратное данному.  a ab c d |
