Пояснительная. Пояснительная записка к курсовой работе по курсу Введение в информатику
 Скачать 1.08 Mb. Скачать 1.08 Mb.
|
|
Министерство образования и науки Украины Донецкий национальный технический университет Кафедра вычислительной математики и программирования Пояснительная записка к курсовой работе по курсу «Введение в информатику» Выполнил студент ЭС 10-а ,ЭТФ Горлакова С.Н. Руководитель работы Кучер Т.В. Донецк 2011 Министерство образования и науки Украины Донецкий национальный технический университет Кафедра вычислительной математики и программирования Задание для курсовой работы по курсу “Введение в информатику ” Тема курсовой работы Использование метода LU-разложения для нахождения значений токов в ветвях электрической цепи Руководитель Кучер Т.В. Донецк 2011 Аннотация В данной курсовой работе методом LU-разложения находятся токи во всех ветвях электрической цепи, а также проверяется баланс мощностей источника и нагрузки. Программа решения задачи написана на языке программирования С++. Исходные данные считываются из текстового файла 1txt, записываются в файл 2.txt. Правильность работы программы проверяется в математическом пакете Scilab. ОглавлениеВведение 5 1.Постановка задачи 6 2.Описание математической модели решения задачи 7 3. Блок-схема алгоритма задачи 8 3.1 Блок-схема метода LU-разложения 8 3.2 Блок-схема функции main 11 4.Описание алгоритма 12 5. Характеристика данных и их условные обозначения 13 6. Текст программы 14 7. Контрольный расчёт с помощью Scilab 19 8. Анализ результатов 20 Заключение 21 Список используемой литературы 22 Приложение 1. Данные программы, хранящиеся в текстовом файле 1.txt 23 Приложение 2. Запись данных и вычислений в текстовый файл 2.txt 25 Приложение 3. Результаты работы программы 26 ВведениеВ данной работе необходимо разработать программу, которая бы рассчитывала токи во всех ветвях электрической цепи, а также проверить баланс мощностей. Использовать для этого метод LU-разложения. Использование математических методов для решения инженерных задач на ЭВМ позволяет значительно увеличить эффективность процессов проектирования, расчетов параметров, исследования, анализа различных технических систем, в том числе и электротехнических.
Определить токи во всех ветвях электрической цепи, проверить баланс мощностей. Для решения задачи воспользоваться методом LU-разложения.  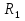 =85Oм, =85Oм, 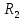 =86Oм, =86Oм, 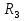 =87Oм, =87Oм, 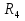 =88Oм, =88Oм, 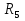 =89Oм, =89Oм, 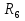 =90Oм, E =90Oм, E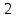 =89В, =89В, 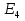 =43В, =43В, 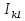 =0.5A. =0.5A.Рисунок 1.1 Электрическая цепь В программе необходимо предусмотреть, откуда будут считываться исходные данные – с диалогового окна или из текстового файла. Результаты вычислений сохранить в текстовом файле 2.txt. Средствами математического пакета проверить результаты работы программы.
Используя второй закон Кирхгофа, составим систему линейных алгебраических уравнений для нахождения значений контурных токов. 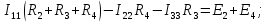 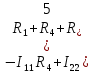 (2.1) (2.1) 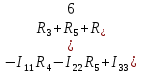 Решив систему (2.1) одним из известных методов, получим значения контурных токов. После чего найдём значения токов в ветвях: 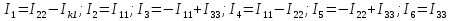 (2.2) Проверим баланс мощностей 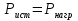 (2.3) (2.3)Мощность источников 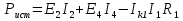 85 85 Мощность нагрузок 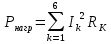 Найти значения токов во всех ветвях электрической цепи (рис.1.1), проверить баланс мощностей (2.3). Для решения системы (2.1) воспользоваться методом LU-разложения. 3. Блок-схема алгоритма задачи3.1 Блок-схема метода LU-разложения Рис.3.1 Блок-схема метода LU-разложения  Блок-схема метода LU-разложения (продолжение) 3.2 Блок-схема функции main Рис.3.2 Блок-схема функции main 4.Описание алгоритмаВ блоке 1 задаётся цикл по строкам матрицы, а в блоке 2 – по столбцам. Блок 3 – условие формирования треугольных матриц. Блоки 4-7– формирование треугольной матрицы U. Блоки 8-11– формирование треугольной матрицы L. Блоки 12-17– формирование вектора вспомогательных переменных Y. Блоки 18-24– нахождение массива неизвестных Х. В блоке 25 вводятся исходные данные Е1, Е4, Ік1, массив R[6]. В блоке 27 выделяется память под матрицу А и вектор В. В блоке 28 ставится условие : при нажатии 1– данные считываются с файла, а при 2 – производится ввод с клавиатуры. В блоках 29-31 вручную вводятся размерность матрицы А, значения Е1, Е4, Ік1 и массива R[6]. В блоке 32 выделяется память под матрицу А и вектор В, происходит их формирование. В блоке 33 вызывается метод LU-разложения. В блоке 34 проверяется баланс мощностей Рi=Pn. Pi=E2*I2+E4*I4-Ik1*I1*R1. Pn= 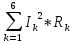 . .5. Характеристика данных и их условные обозначения
6. Текст программы#include #include #include #include using namespace std; int metod_LU(float **A,float*B,int n,float *x) { int i,j,k; float **U,**L,*y; y=new float[n]; // b=new float[n]; U=new float *[n]; L=new float *[n]; for(i=0;i { U[i]=new float [n]; L[i]=new float [n]; } float S; for(i=0;i for(j=0;j { U[0][i]=A[0][i]; L[i][0]=A[i][0]/U[0][0]; if(i<=j) { S=0; for(k=0;k S=S+L[i][k]*U[k][j]; U[i][j]=A[i][j]-S; } else U[i][j]=0; if (i>j) { S=0; for(k=0;k S=S+L[i][k]*U[k][j]; if(U[j][j]==0) return 0; else L[i][j]=(A[i][j]-S)/U[j][j]; } else L[i][j]=0; } cout<<"\n U"; for (i=0; i for (j=0; j cout< cout<<"\n L"; for (i=0; i for (j=0; j cout< y[0]=B[0]; for(i=1;i { S=0; for(k=0;k<=i;k++) S=S+L[i][k]*y[k]; y[i]=(B[i]-S); } if(U[n-1][n-1]==0) return 0; else x[n-1]=y[n-1]/U[n-1][n-1]; for(i=n-2;i>=0;i--) { S=0; for(k=i+1;k S=S+U[i][k]*x[k]; if(U[i][i]==0) return 0; else x[i]=(y[i]-S)/U[i][i]; } return 1; } int main() { int i,j, m,n,k; float **A,*B,*x,*I,Pi,Pn, R1,R2,R3,R4,R_4,R5,R6,R_6,E2,E3,Ik2,Ir2,rez,I1,I2,I3,I4,I5,I6; ifstream f; ofstream f1; cout<<"Vvedite 1-esli vvod iz faila,2-esli s klaviaturi"; cin>>m; if(m==1) { f.open("F:\\kurs\\1.txt",ios::in); if(f) { f>>n; I=new float [n]; f>>R1; f>>R2; f>>R3; f>>R4; f>>R_4; f>>R5; f>>R6; f>>R_6; f>>E2>>E3>>Ik2; f.close(); } else { cout<<"Not file"; return 0; } } else { cout<<"Vvedite R \n"; n=7; cout<<"R1"; cin>>R1; cout<<"R2"; cin>>R2; cout<<"R3"; cin>>R3; cout<<"R4"; cin>>R4; cout<<"R_4"; cin>>R_4; cout<<"R5"; cin>>R5; cout<<"R6"; cin>>R6; cout<<"R_6"; cin>>R_6; cout<<"E2=";cin>>E2; cout<<"E3=";cin>>E3; cout<<"Ik2=";cin>>Ik2; } A=new float*[n]; for(i=0;i A[i]=new float[n]; A[0][0]=-1; A[0][1]=1; A[0][2]=0; A[0][3]=0; A[0][4]=1; A[0][5]=0; A[0][6]=0; A[1][0]=0; A[1][1]=0; A[1][2]=1; A[1][3]=1; A[1][4]=-1; A[1][5]=0; A[1][6]=0; A[2][0]=0; A[2][1]=1; A[2][2]=-1; A[2][3]=0; A[2][4]=0; A[2][5]=1; A[2][6]=0; A[3][0]=0; A[3][1]=1; A[3][2]=0; A[3][3]=0; A[3][4]=0; A[3][5]=0; A[3][6]=-1; A[4][0]=0; A[4][1]=0; A[4][2]=R3; A[4][3]=-1*(R4+R_4); A[4][4]=0; A[4][5]=((R6*R_6)/(R4+R_4)); A[4][6]=0; A[5][0]=R1; A[5][1]=0; A[5][2]=R3; A[5][3]=0; A[5][4]=R5; A[5][5]= ((R6*R_6)/(R4+R_4)); A[5][6]=0; A[6][0]=-R1; A[6][1]=R2; A[6][2]=0; A[6][3]=0; A[6][4]=0; A[6][5]=-1*((R6*R_6)/(R4+R_4)); A[6][6]=0; B=new float [n]; B[0]=0; B[1]=0; B[2]=0; B[3]=Ik2; B[4]=E3; B[5]=E3; B[6]=E2; x=new float [n]; rez=metod_LU(A,B,n,x); if(rez==1) { I1=x[0]; I2=x[1]; I3=x[2]; I4=x[3]; I5=x[4]; I6=x[5]; Ir2=I2-Ik2; cout<<"\nI1="< cout<<"\nI2="< cout<<"\nI3="< cout<<"\nI4="< cout<<"\nI5="< cout<<"\nI6="< cout<<"\nIr2="< Pi= E2*I2+E3*I3-R2*I2*Ik2;cout<<"\nPi="< Pn=R1*I1*I1+R2*I2*I2+R3*I3*I3+R4*I4*I4+ R5*I5*I5+R6*I6*I6; cout<<"\nPn="< } else cout<<"\n metod eror"; f1.open("F:\\kurs\\2.txt",ios::out); f1<<"\n Znachenie tokov \n"; for(i=0;i f1< f1<<"\n Moshnost istochnikov toka Pist="< f1<<"\n Moshnost nagruzok Pnagr="< system("PAUSE"); return EXIT_SUCCESS; } 7. Контрольный расчёт с помощью Scilab-->A=[R2+R3+R4,-R4,-R3;-R4,R1+R4+R5,-R5;-R4,-R5,R3+R5+R6] A = 261. - 88. - 87. - 88. 262. - 89. - 88. - 89. 266. -->B=[E2+E4;-E4+Ik1*R1;0] B = 132. - 0.5 0. -->x=inv(A)*B x = 0.7615859 0.3830105 0.3801034 -->R=A*x R = 132. - 0.5 0. Pn=89.32142 Pi=89.031938 8. Анализ результатовВ результате работы данной программы были получены следующие значения контурных токов в цепи: I[0]=-0.0616148 I[1]=0.757867 I[2]=-0.444932 I[3]=0.319481 I[4]=-0.125451 I[5]=0.312934 Pi=83.8065 Pn=85.8142 Мощность источника и мощность нагрузки приблизительно одинаковы. Правильность работы данной программы проверена с помощью математического пакета Scilab. ЗаключениеВ результате курсовой работы я закрепила теоретические знания и практические навыки по курсу «Введение в информатику». При выполнении курсовой работы мною была разработана программа на языке C++, которая позволяет вычислять значения контурных токов во всех ветвях элкетрической цепи, при помощи метода LU-разложения. А также проверенна правильность работы программы в математическом пакете Scilab. Список используемой литературы
Приложение 1. Данные программы, хранящиеся в текстовом файле 1.txt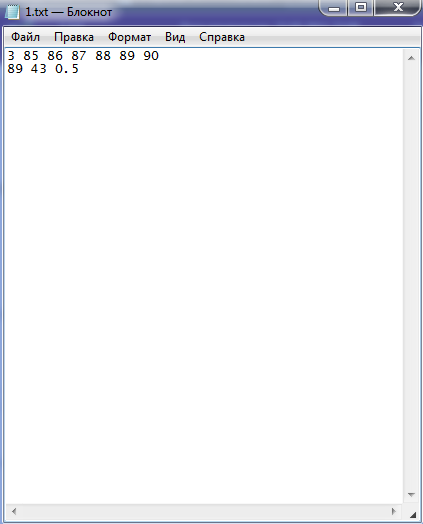 Приложение 2. Запись данных и вычислений в текстовый файл 2.txt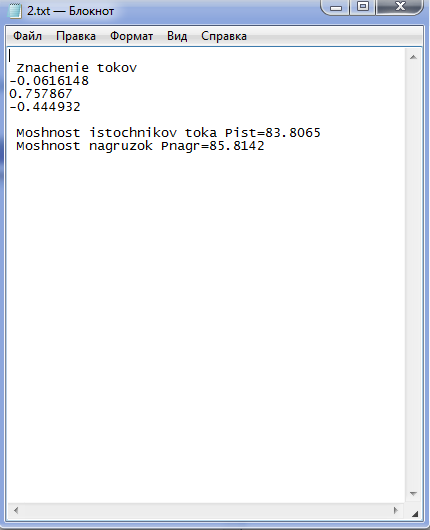 Приложение 3. Результаты работы программы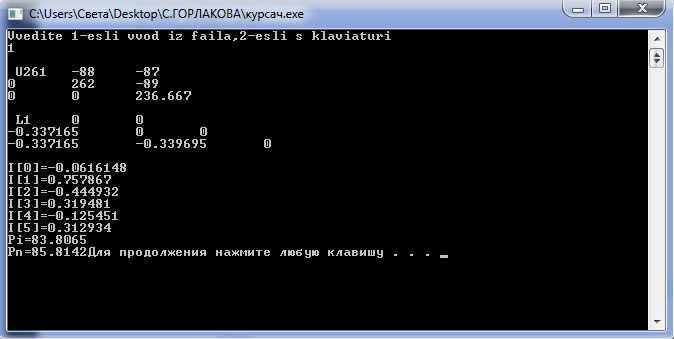 Приложение 4. Проверка программы в Scilab 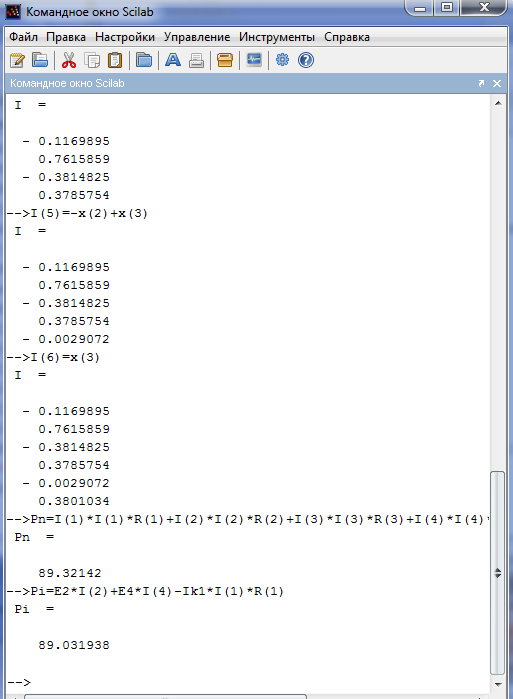 |
