практическая работа. практическая работа exel. Практическая работа На протяжении последних занятий мы с вами изучали тему Электронные таблицы
 Скачать 0.98 Mb. Скачать 0.98 Mb.
|
|
Практическая работа № На протяжении последних занятий мы с вами изучали тему «Электронные таблицы». Познакомились с табличным процессором. И узнали о широких возможностях, реализованных в нём. Вопросы: · повторение основных приёмов работы с электронными таблицами; · примеры использования электронных таблиц при решении задач по конкретным школьным предметам. Как вы помните, использование электронных таблиц существенно облегчает решение расчётных задач. Особенно, если решение громоздкое. Например, в химии – в задачах о растворах. Или в физике – в задачах о тепловых явлениях. Ход решения при этом соответствует этапам традиционного способа решения задачи: анализ условия и требуемых закономерностей, ввод исходных данных, ввод требуемых формул, получение и анализ результатов. Пример 1. Решение задачи по математике. Известны длины трёх оград, возведённых вокруг земельного участка треугольной формы. Длина первой ограды 12 м, второй – 7 м и третьей – 9 м. Необходимо определить периметр участка и его площадь. Перед нами таблица «Земельный участок». 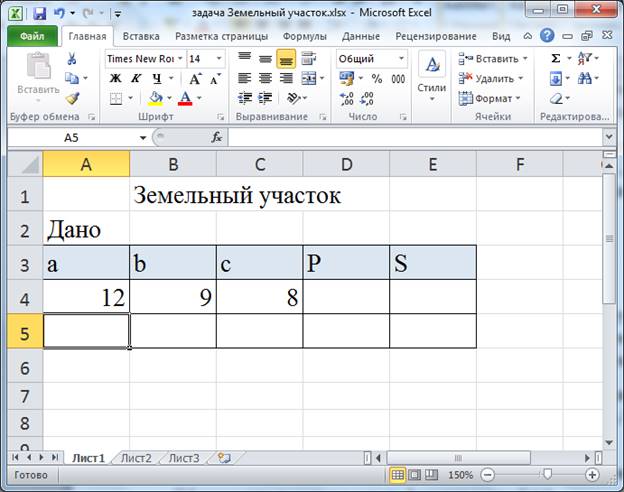 В ячейку D4 введем формулу для вычисления периметра треугольника. Равно А4+В4+С4 и нажимаем Enter. Отметим также, что здесь в качестве формулы для вычисления периметра участка можно использовать и функцию СУММ. 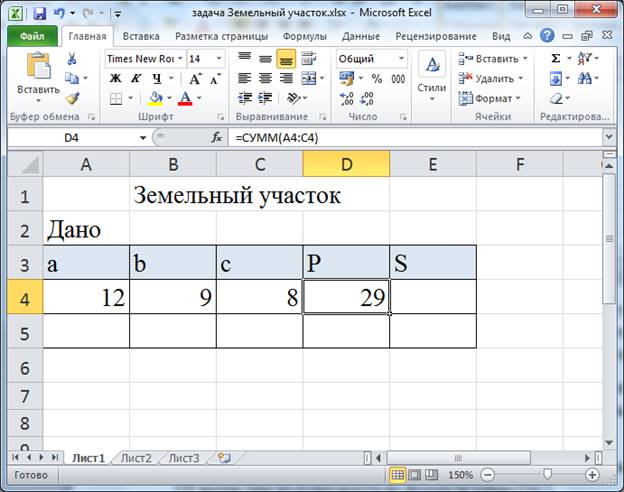 В данной задаче для нахождения площади треугольника нужно применить формулу Герона. Здесь p – это полупериметр, a, b и с – длины сторон треугольника. Чтобы не загромождать формулу дополнительными вычислениями, в ячейке D5 вычислим полупериметр, разделив значение из ячейки D4 на 2. Теперь в ячейке Е4 запишем формулу для вычисления площади треугольника =КОРЕНЬ(D5*(D5–A4)*(D5–B4)*(D5–C4)).  Ответ: периметр участка равен 28 м, а его площадь 31,3 м2. Отметим преимущество решения задачи именно средствами электронных таблиц, если мы заменим исходные данные, то сразу же получим новый верный ответ. Обратите внимание. При решении данной задачи мы вспомнили: Правила ввода формул, а именно: · формулу начинают со знака «равно», завершают нажатием клавиши Enter или щелчком мыши по свободной ячейке и другие способы; · используются числа, знаки операций, ссылки и функции; · порядок выполнения действий не отличается от принятого в математике. Также вспомнили относительные ссылки. Относительные ссылки – это ссылки в формулах, которые изменяются при копировании. В нашем примере мы также использовали встроенные функции. Встроенные функции – это функции, которые уже содержатся в табличном процессоре и выполняют различные вычисления автоматически при их вызове из библиотеки функций. Каждая функция имеет свое собственное имя, которое необходимо для ее вызова. Имя функции – это не что иное, как сокращение от названия функции. Например, в нашем примере использовалась функция «корень» в табличном процессоре она так и называется: КОРЕНЬ. Использование электронных таблиц оказывается незаменимым при выполнении многократно повторяющихся вычислений и исследовании зависимостей в различных предметных областях. Пример 2. Создать таблицу для расчёта стоимости проезда на автомобиле в зависимости от расстояния, цены и расхода топлива. Введём значения расхода топлива и его цены в ячейки A2 и B2. Диапазон ячеек A5:A16 заполним рядом значений расстояний от 10 до 120 км с шагом 10. 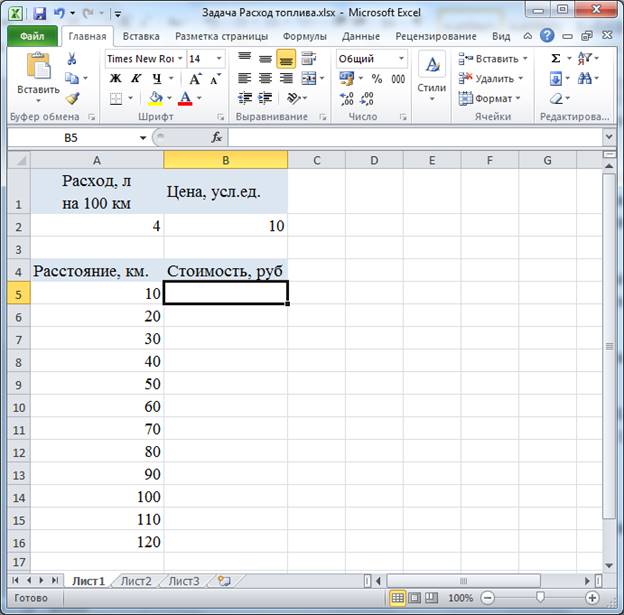 В ячейку B5 введём формулу, содержащую абсолютные ссылки для расчёта стоимости проезда =$A$2*$B$2*A5/100. 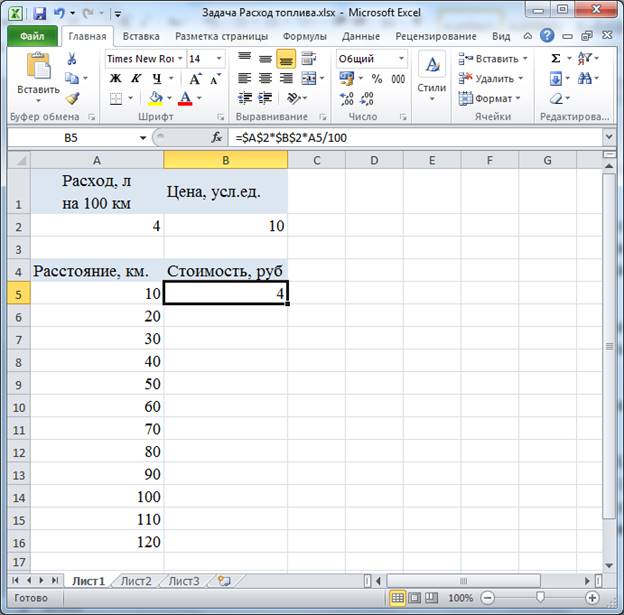 Распространим эту формулу на диапазон В5:В16.  Получим таблицу значений. Изменяя значения расхода топлива и цены, будем получать стоимость проезда в зависимости от расстояния. Обратите внимание. При решении данной задачи мы вспомнили: Абсолютные ссылки – это ссылки в формулах, которые не изменяются при копировании. Смешанные ссылки – это ссылки в формулах, содержащие абсолютную и относительную части. Пример 3. В классе в конце года были проведены тесты по четырём предметам: физике, математике, информатике и русскому языку. Результаты тестирования приведены в таблице. По результатам тестирования проводится отбор в физико-математический класс. Зачисляются те ученики, у кого общий балл по предметам не ниже 16, а суммарный балл по физике и математике не ниже 9. В Отметке о зачислении должна быть запись «да» или «нет». Также подсчитать число учащихся, принятых в физико-математический класс. Итак, перед нами таблица результатов тестирования.  Здесь нам нужно применить формулу, которая будет содержать две логические функции: ЕСЛИ и функцию И. Напомним: Функция ЕСЛИ проверяет, выполняется ли условие, и возвращает значение ИСТИНА, если оно выполняется, и значение ЛОЖЬ, если нет. Функцию ЕСЛИ ещё называют условной функцией. Функция И применяется для расширения возможностей других функций, выполняющих проверку. Она возвращает значение ИСТИНА, если в результате вычисления всех аргументов получается значение ИСТИНА; возвращает значение ЛОЖЬ, если в результате вычисления хотя бы одного из аргументов получается значение ЛОЖЬ. В ячейку F3 запишем формулу =ЕСЛИ(И(СУММ(B3:E3)>=16;СУММ(B3:C3)>=9);"Да";"Нет"). Скопируем формулу в диапазон F4:F7. 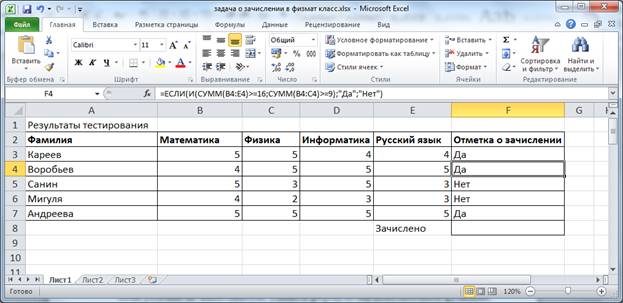 Здесь функция ЕСЛИ проверяет выполнение условий для зачисления учащихся и возвращает значение «да» если условие выполняется и «нет», если условие не выполняется. Также в формуле мы использовали функцию И, которая объединила два условия необходимых для зачисления учащихся. Теперь в таблице мы видим отметку о зачислении учащихся в физико-математический класс. Также нам нужно посчитать число учащихся, принятых в физико-математический класс. Для этого используем функцию СЧЁТЕСЛИ. Функция СЧЁТЕСЛИ используется, если требуется подсчитать только те числа, которые соответствуют определенным критериям. В ячейку F8 запишем формулу =СЧЁТЕСЛИ(F3:F7;"Да"). Здесь на первом месте мы указали диапазон ячеек, который необходимо посчитать, а на втором месте – условие для счёта.  В результате мы получили ответ. Пример 4. Пользуясь данными, приведёнными в таблице, нужно построить лепестковую диаграмму, отображающую направление ветров. 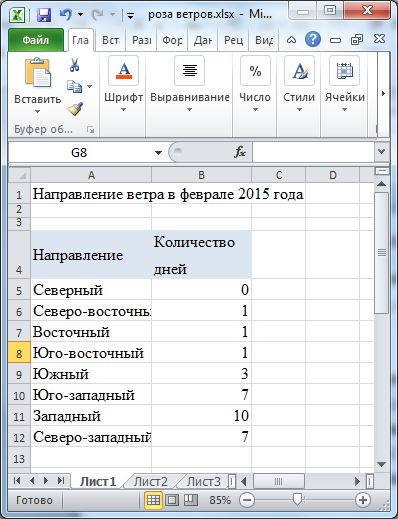 Перед нами таблица. Теперь для построения лепестковой диаграммы выделим диапазон ячеек А4:В12. На вкладке «Вставка» в разделе «Диаграммы» нажмём на значок раскрывающегося меню «Другие». В раскрывшемся меню выберем тип диаграммы «Лепестковая», вид также «Лепестковая». Отредактируем полученную диаграмму. Исправим заголовок. 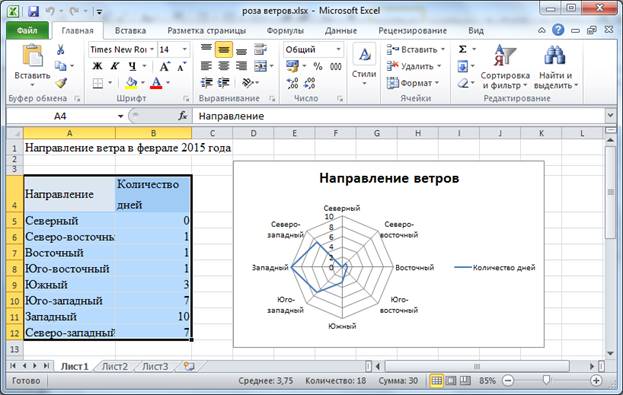 Мы построили розу ветров, по которой можно сказать, что феврале преобладал западный ветер, а северного не было вообще. Пример 5. Очень часто в жизни, особенно в период заготовок на зиму солений, приходится решать следующие задачи: В сосуде, содержится 200 г 70 % -го раствора уксусной кислоты. В него добавили 1550 г воды. Нужно определить массовую долю уксусной кислоты в получившемся растворе. Заполним таблицу исходными данными.  В химии массовой долей вещества в растворе называют отношение массы растворенного вещества к массе раствора и выражают в процентах. Отсюда получим формулу расчёта массы уксусной кислоты. Введём эту формулу в ячейку В5 =B2*B3/100.  В ячейке С2 вычислим суммарную массу раствора: =B2+B4. 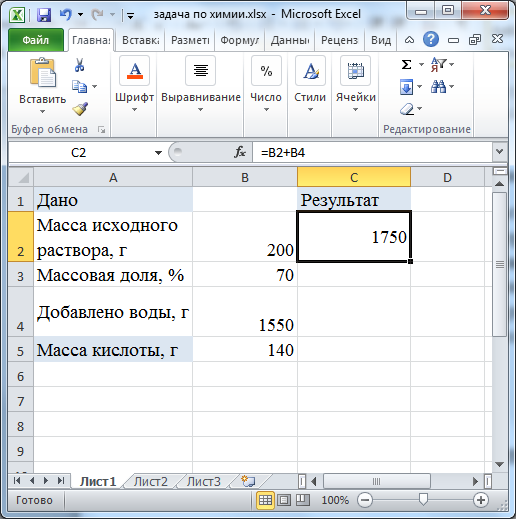 Наконец в ячейке С3 вычислим массовую долю кислоты в полученном растворе: =100*B5/C2. 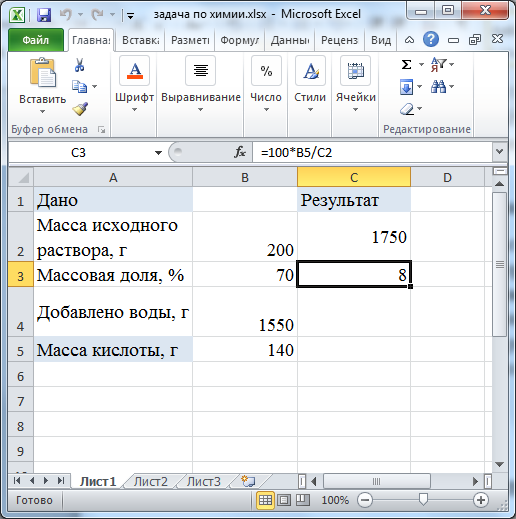 В результате мы получим ответ 8 %. Пример 6. Рассмотрим задачу по физике. В теплоизолированный сосуд, в котором находится 500 г воды при температуре 30 °С, бросают кусок льда массой 50 г, имеющий температуру 0 °С. Какой станет температура воды после плавления льда и установления теплового равновесия? Введем данные условия задачи в ячейки B2:B5. 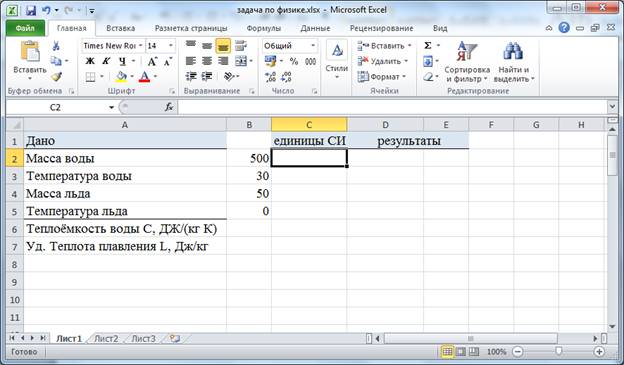 В ячейках С2:С5 приведем их к системе СИ: 1 кг равен 1000 г, 1 К равен 1 °С + 273.  Искомую температуру определим из уравнения теплового баланса. Массу воды после плавления льда вычислим в ячейке D2: =C2+C4, а температуру в Кельвинах — в ячейке D3 по формуле =(C6*C2*C3+C6*C4*C5–C7*C4)/(C6*D2).  Полученную температуру пересчитаем в градусы Цельсия в ячейке Е3.  Так, в нашем примере температура воды после плавления льда станет 20,13 градуса Цельсия. |
