Практическая работа 2 по теме Пирамида

• Название: Практическая работа 2 по теме Пирамида
• Дата: 20.02.2023
• Размер: 157.38 Kb.
• Имя файла: Prakticheskaya_rabota_Piramida.docx
• Тип: Практическая работа; #946604

Практическая работа № 2 по теме: «Пирамида»

Цели: закрепление понятий: пирамида, площадь боковой и полной поверхности пирамиды; воспитание познавательной активности , показать возможность применения пирамиды в различных областях.

Оборудование: модели пирамид, таблица с формулами S_б.п., S_п.п., линейки, карандаши, калькулятор.

Методические указания.

Пирами́да — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные, четырёхугольные и т. д.

наклонная прямая



Элементы пирамиды.

Д – высота пирамиды

ДВ, ДС, ДА - боковые ребра — общие стороны боковых граней;

ДВА, ДАС, ДВС - боковые грани — треугольники, сходящиеся в вершине пирамиды

ДК, ДL - апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины [ℓ]; ДN- высота пирамиды.

П ирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания. Тогда она обладает такими свойствами:

боковые ребра правильной пирамиды равны; в правильной пирамиде все боковые грани — равные равнобедренные треугольники; в любую правильную пирамиду можно как вписать, так и описать около неё сферу;

Прямоугольная пирамида

Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В данном случае, это ребро и является высотой пирамиды.

У сечённая пирамида
Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.

Боковая поверхность — это сумма площадей боковых граней.

Для нахождения боковой поверхности в правильной пирамиде можно использовать формулу:

S_б.п.= 1/2•Р•ℓ, где Р – периметр основания.

Полная поверхность — это сумма площади боковой поверхности и площади основания.

Для нахождения полной поверхности в правильной пирамиде можно использовать формулу:

S_п.п. = 1/2•Р•ℓ+S_осн.
Задание к практической работе: по данным вам моделям найти площадь боковой, полной поверхности. Выполнить тесты.
Пример: Найти площадь боковой, полной поверхности.

Ход работы

1. По предложенной развертке (в конце работы) склейте фигуру. Для нахождения площади боковой поверхности пирамиды нужно измерить линейкой следующие элементы:

• 
  апофему,
  
• 
  стороны основания,
  
• 
  высоту.
  

Подставить значения в формулу для нахождения пощади (если пирамида правильная).

Если нет возможности распечатать развертку пирамиды и склеить ее, задайте параметры фигуры произвольно, как показано в примере.

2. Для нахождения площади полной поверхности пирамиды нужно найти площадь основания пирамиды (площадь треугольника, прямоугольника, ромба)

3.Площадь полной поверхности пирамиды находиться как сумма площадей боковой поверхности и основания.

Оформление работы:

	Дано: SАВСД – пирамида, АВСД –прямоугольник. АВ=3см, ВС= 6см, Н=10см, ℓ1=10,5см., ℓ2=10,2см , ℓ- апофема. Найти: Sб.п. Sп.п. Решение. т.к. пирамида неправильная, то Sб.п. находят как сумму площадей ее боковых граней, т.е. площадей треугольников. S1 = 1/2 ·ℓ1·АВ=1/2·10,5·3=15,75(см2) - это площадь одной грани, а их две одинаковых, т.е S1,2 =15,75·2=31,5(см2)
S3=1/2·ℓ2·ВС= 1/2·10,2·6=30,6 (см2), S3,4=2·30,6=61,2(см2) Sб.п.= 31,5+61,2 =92,7(см2) Sосн.= АВ·ВС=3·6=18(см2), Sп.п.= Sб.п+ Sосн.= 92,7+18=110,7 (см2)

Задания для самостоятельной работы:

1. Сколько ребер у шестиугольной пирамиды: а)6; б)12; в)18; г)24;

2. Какое наименьшее число граней может иметь пирамида: а)5; б)4 в)10; г)6

3. Подтвердите или опровергните следующие утверждения: Да ^ нет

а) Многогранник, составленный из n-треугольников, называется пирамидой; б) Пирамида называется правильной, если ее основание – правильный многоугольник; в) Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой;

4.Задача. Крыша башни имеет вид правильной четырехугольной пирамиды, у которой сторона основания равна 12 м, а высота 18 м. Сколько понадобится плиток на покрытие этой крыши, если каждая плитка имеет вид прямоугольника со сторонами 22 см и 18 см.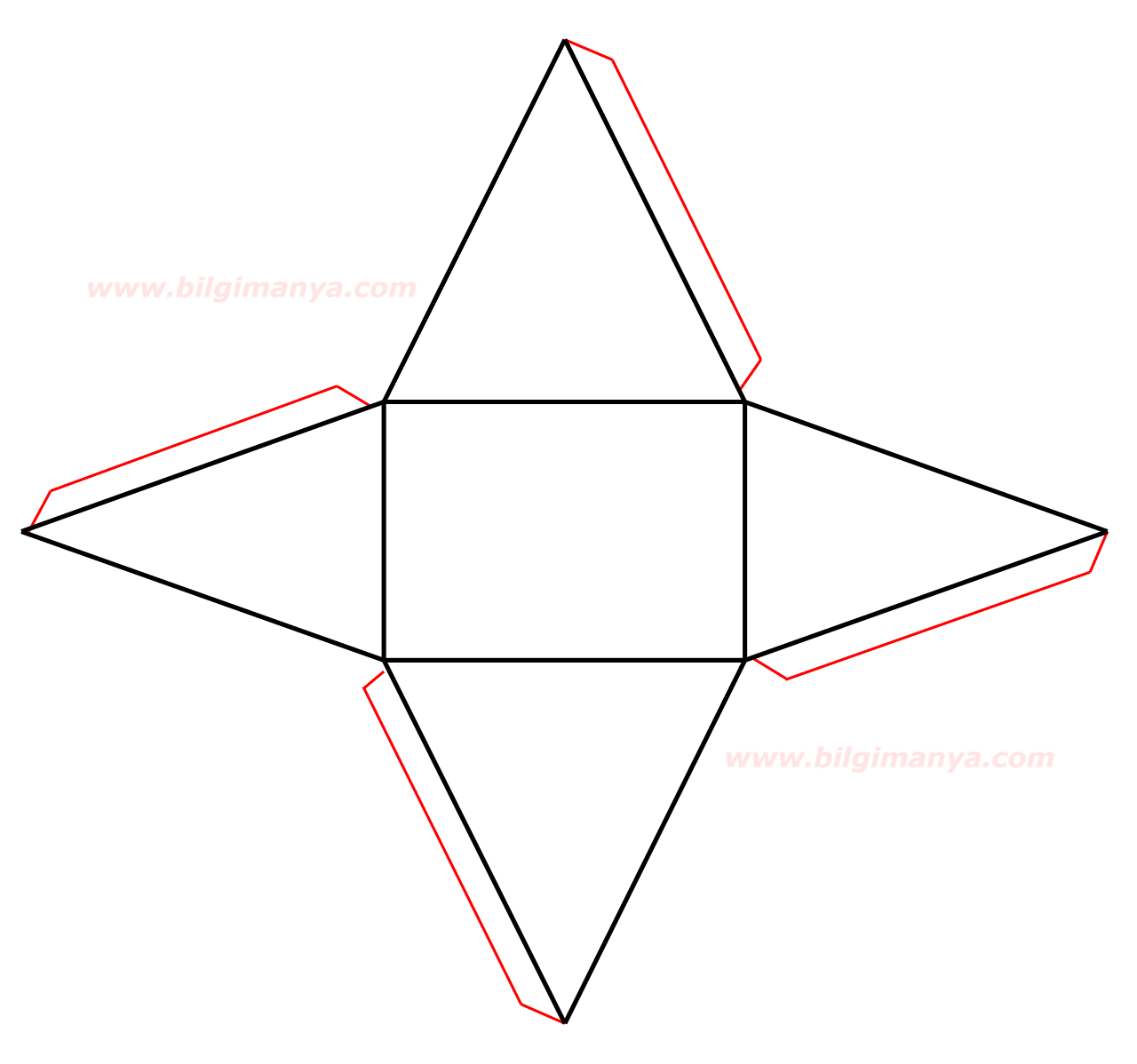