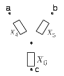
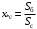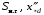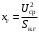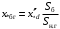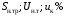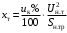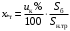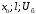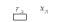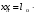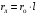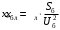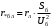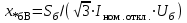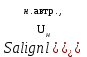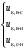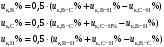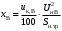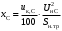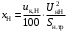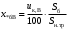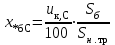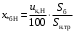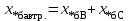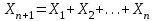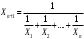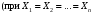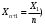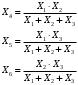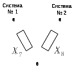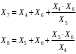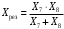Расчёт результирующего сопротивление внешнего электроснабжения. Практическое задание 1 Расчёт результирующего сопротивление внешнего электроснабжения
 Скачать 0.75 Mb. Скачать 0.75 Mb.
|
|
ПРАКТИЧЕСКОЕ ЗАДАНИЕ №1 Расчёт результирующего сопротивление внешнего электроснабжения Основой расчёта результирующего сопротивления внешнего электроснабжения является приведение сопротивлений всех элементов схемы к базисным условиям Sб, Uб = Uн(ср.ступени), где Sб – базисная мощность;Uб – базисное напряжение. Причем обычно произвольно задают Sб, а Uб принимают равным среднему напряжению ступени элемента, для которого рассчитывается сопротивление. Расчетные напряжения выше номинальных примерно на 5 %. Так, для номинальных напряжений На рисунке 1 представлена примерная схемы внешнего электроснабжения. Из схемы видно, что на двух подстанциях произошло короткое замыкания. 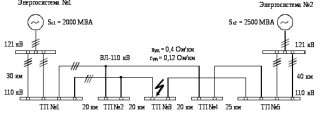 Рис.1 Схема внешнего электроснабжения Ток находят по формуле мощности: 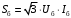 , (1) , (1)откуда: 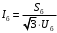 . (2) . (2)Принимается определенное значение базисной мощности 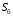 , МВА (обычно принимают , МВА (обычно принимают 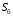 = 100 МВА). = 100 МВА).По расчетной схеме составляется схема замещения, на которой каждый элемент изображается эквивалентным сопротивлением Z или Х рисунок 2. 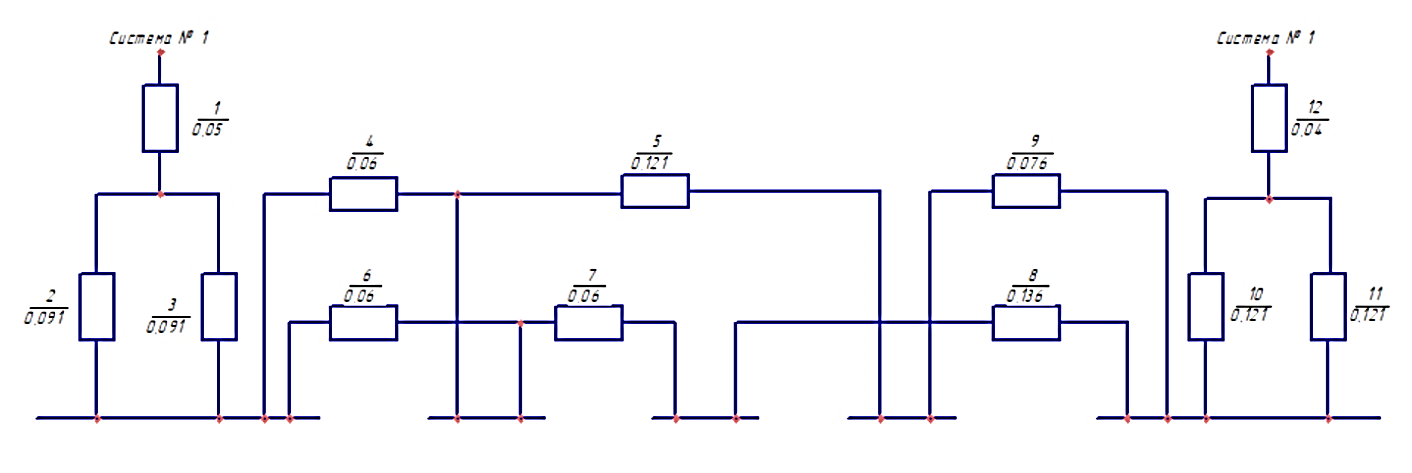 Рис. 2. Схема замещения транзитной подстанции Ток находят по формуле мощности: 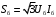 . .В основе формул вычисления r, x и z лежит соотношение 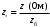 ; ; 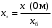 ; ; 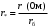 , ,где z(Ом) – полное сопротивление в именованных единицах; х (Ом) – индуктивное сопротивление в именованных единицах; r (Ом) – активное сопротивление в именованных единицах; 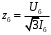 , , 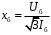 , ,где «б» – базисное условие. Если r >1/3х, то должны быть определены активные и индуктивные составляющие полного сопротивления цепи к.з. Послеопределения всех сопротивлений цепи необходимо найти полное общее сопротивление 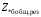 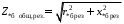 . (3) . (3)Если 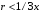 , то активными сопротивлениями пренебрегают, и учитывают только индуктивные сопротивления, что часто имеет место в высоковольтных цепях. , то активными сопротивлениями пренебрегают, и учитывают только индуктивные сопротивления, что часто имеет место в высоковольтных цепях.Выражения для определения сопротивлений в именованных и относительных единицах для различных элементов цепи к.з. приведены в табл. 1 Таблица 1 Расчет сопротивлений элементов схемы замещения
В табл. 1 приведены обозначения следующих параметров: 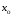 – индуктивное сопротивление 1 км линии, Ом/км; l – длина линии, км; – индуктивное сопротивление 1 км линии, Ом/км; l – длина линии, км; 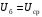 – среднее расчётное напряжение линии, кВ; – среднее расчётное напряжение линии, кВ; 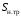 – номинальная мощность трансформатора, МВА; – номинальная мощность трансформатора, МВА; 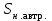 – номинальная мощность автотрансформатора, МВА; – номинальная мощность автотрансформатора, МВА; 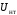 – номинальное напряжение трансформатора, кВ; – номинальное напряжение трансформатора, кВ; 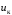 % – напряжение к.з. для каждой пары обмоток, %; % – напряжение к.з. для каждой пары обмоток, %; 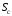 – мощность системы, МВА; – мощность системы, МВА; 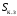 – мощность короткого замыкания системы, МВА; – мощность короткого замыкания системы, МВА; 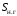 – номинальная мощность генератора, МВА; – номинальная мощность генератора, МВА; 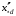 – относительное сверхпереходное индуктивное сопротивление генератора по продольной оси. – относительное сверхпереходное индуктивное сопротивление генератора по продольной оси.Путем постепенного преобразования схемы замещения по правилам, известным из курса ТОЭ (табл. 2), приводят схему замещения к наиболее простому виду так, чтобы каждый источник питания или группа источников были связаны с точкой к.з. одним результирующим сопротивлением 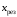 (рис. 2, 3). Расчет ведется по общему или индивидуальным изменениям тока к.з. (рис. 2, 3). Расчет ведется по общему или индивидуальным изменениям тока к.з.Таблица 2 Преобразование схемы замещения
Примечание. В обозначениях относительных сопротивлений индексы (*) и «б» (базисные единицы) опущены. Расчёта токов к.з. в точке К-21. Исходные данные берутся из задания. Вычерчиваем расчетную однолинейную схему питания тяговой подстанции (см. рис. 1). Ниже вводов изображаем понижающие трансформаторы и РУ, от которых питается районная нагрузка и ТСН (необходимо для последующих расчетов). В данном случае от РУ-10 кВ (по условиям задания) вместе с районной нагрузкой питается электрическая тяга, а также собственные нужды. 2. Выбираем базисные условия – 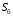 = 100 МВА, тогда при к.з. в точке К-1 = 100 МВА, тогда при к.з. в точке К-1 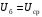 = 115 кВ. = 115 кВ.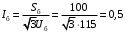 кА. кА.Для этих условий вычисляем относительные сопротивления элементов схемы замещения. Так как для большинства элементов 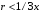 , то учитываем только индуктивные сопротивления элементов: , то учитываем только индуктивные сопротивления элементов: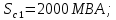 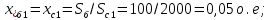 (*-относительные единицы, б-базесные,1- номер расчётного сопротивления, округлять до третьего знака после запятой); (*-относительные единицы, б-базесные,1- номер расчётного сопротивления, округлять до третьего знака после запятой);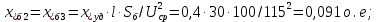 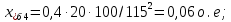 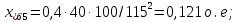 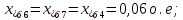 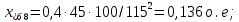 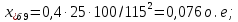 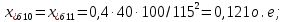 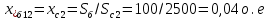 4. Производим последовательные преобразования исходной схемы в упрощенную схему. Находим сопротивления элементов схемы:  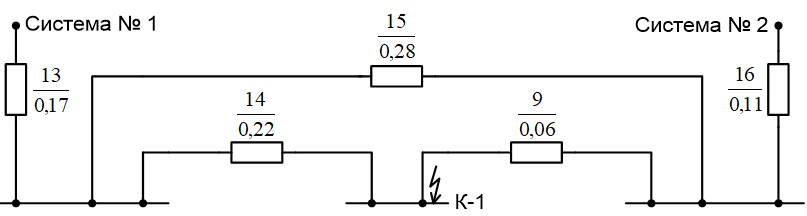 Рис. 3.Схема треугольника сопротивлений. 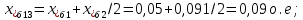 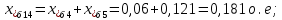 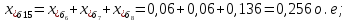 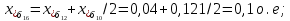 Преобразовав «треугольник» сопротивлений Х14, Х15, Х9 в эквивалентную «звезду», получим схему:   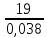 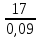    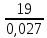 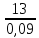 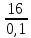 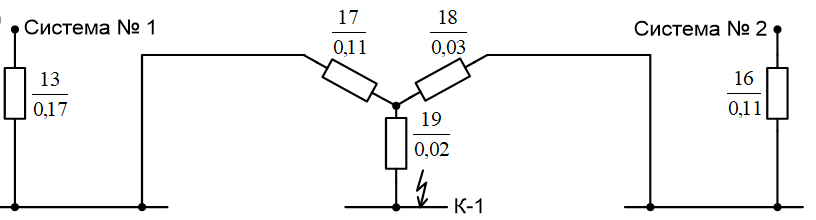 Рис. 4.Схема трехлучевой звезды. 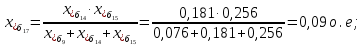 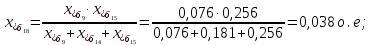 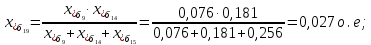 Просуммировав сопротивления 13 и 17, а также 16 и 18, получим трехлучевую «звезду» с сопротивлениями:  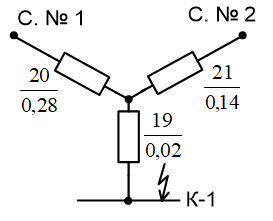 Рис. 5.Схема трехлучевой звезды. 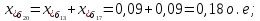 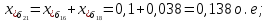 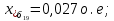 . .Преобразовав трехлучевую «звезду» в двухлучевую, получим:  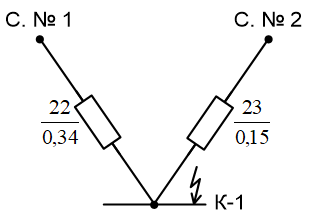 Рис. 6. Схема двухлучевой звезды. 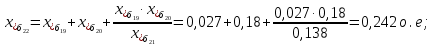 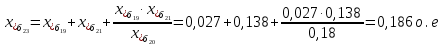 Преобразовав двухлучевая звезда в результирующее сопротивление:  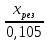 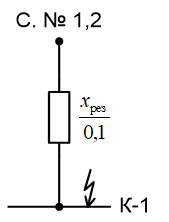 Рис. 7. Результирующее сопротивление. 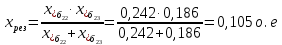 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||