12 Дискриминантный анализ (2022). Практикум Для студентов iiiv курсов дневного и заочного отделений геологического факультета по дисциплине Математические методы в геологии
 Скачать 1.15 Mb. Скачать 1.15 Mb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Пермский государственный национальный исследовательский университет» ДИСКРИМИНАНТНЫЙ анализ Практикум Для студентов II–IV курсов дневного и заочного отделений геологического факультета по дисциплине «Математические методы в геологии» направления подготовки «Геология»(бакалавры) и специальности «Прикладная геология» Пермь 2022 Составитель: ст. преподаватель каф. Поисков и разведки полезных ископаемых Брюхов Виталий Нниколаевич Издание содержит теоретические сведения и подробные рекомендации для выполнения лабораторных заданий по теме: «Дискриминантного анализа многомерной статистической совокупности» в среде Microsoft Excel. Предназначено для студентов II–IV курсов дневного и заочного отделений геологического факультета по дисциплине «Математические методы в геологии» направления подготовки 05.03.01 «Геология» (бакалавры) и специальности 21.05.02 «Прикладная геология». Дискриминантный анализ многомерной модели При изучении сложных геологических объектов часто возникает необходимость их классификации, т.е. отыскания некоторого правила разделения объектов на отдельные однородные группы. Эта группа геологических задач, получившая название распознавания образов, включает решение таких вопросов, как разделение нефтеносных и водоносных пластов (без их опробования), продуктивных и «пустых» структур и т.д. Задача: Определить принадлежность 18 прогнозных структур к группе месторождений или группе пустых структур с помощью дискриминантного анализа по эталонным выборкам. Первая группа (выборка) включает 15 известных нефтяных месторождений (выборка А), вторая группа – 15 заведомо пустых структур (выборка В) Требуется: 1) рассчитать уравнение линейной дискриминантной функции трех переменных (оцениваемых параметров) для разделения исходных данных на две самостоятельные выборки. Оцениваемыми параметрами являются: а) амплитуда структуры (м), б) мощность продуктивной толщи на месторождениях и мощность прогнозируемой толщи на пустых структурах (м), в) коэффициент песчанистости, характеризующий коллекторские свойства продуктивной и прогнозируемой толщи структур. (Под коэффициентом песчанистости понимается отношение суммарной эффективной толщины проницаемых прослоев в продуктивной (или прогнозируемой) толще к общей мощности продуктивной толщи).; 2) разделить прознозные структуры на пустые и нефтеносные путем сравнения дискриминантного индекса и расчетных значений дискриминантной функции. АЛГОРИТМ ВЫПОЛНЕНИЯ ЗАДАНИЯ. Скопируйте исходные значения выборок А и В из вкладки «Данные» в таблицу 1 в соответствии со своим вариантом. 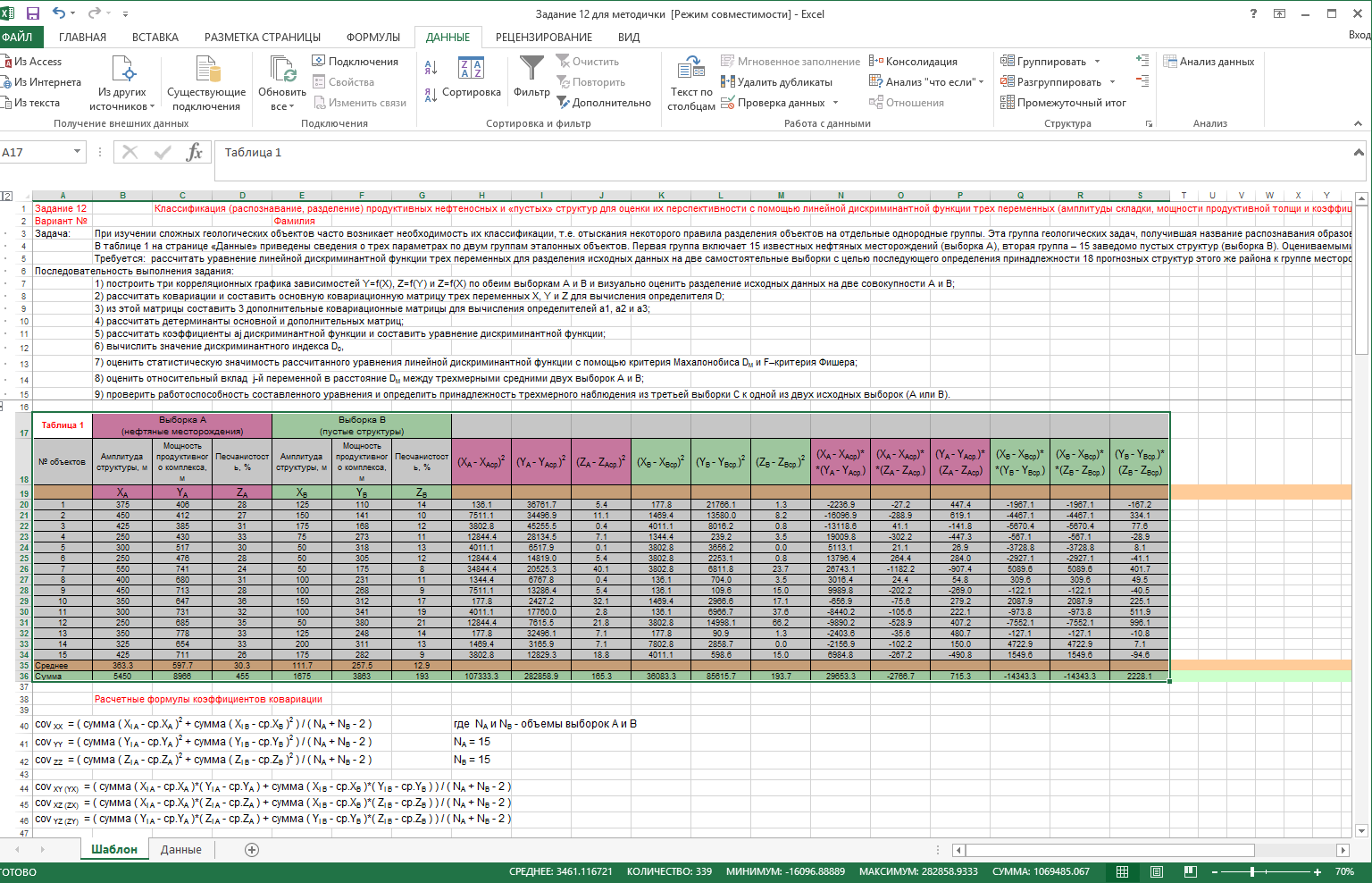 Построение корреляционных полей построить три корреляционных графика зависимостей Y=f(X), Z=f(Y) и Х=f(Z) по обеим выборкам А и В и визуально оценить разделение исходных данных на две совокупности;   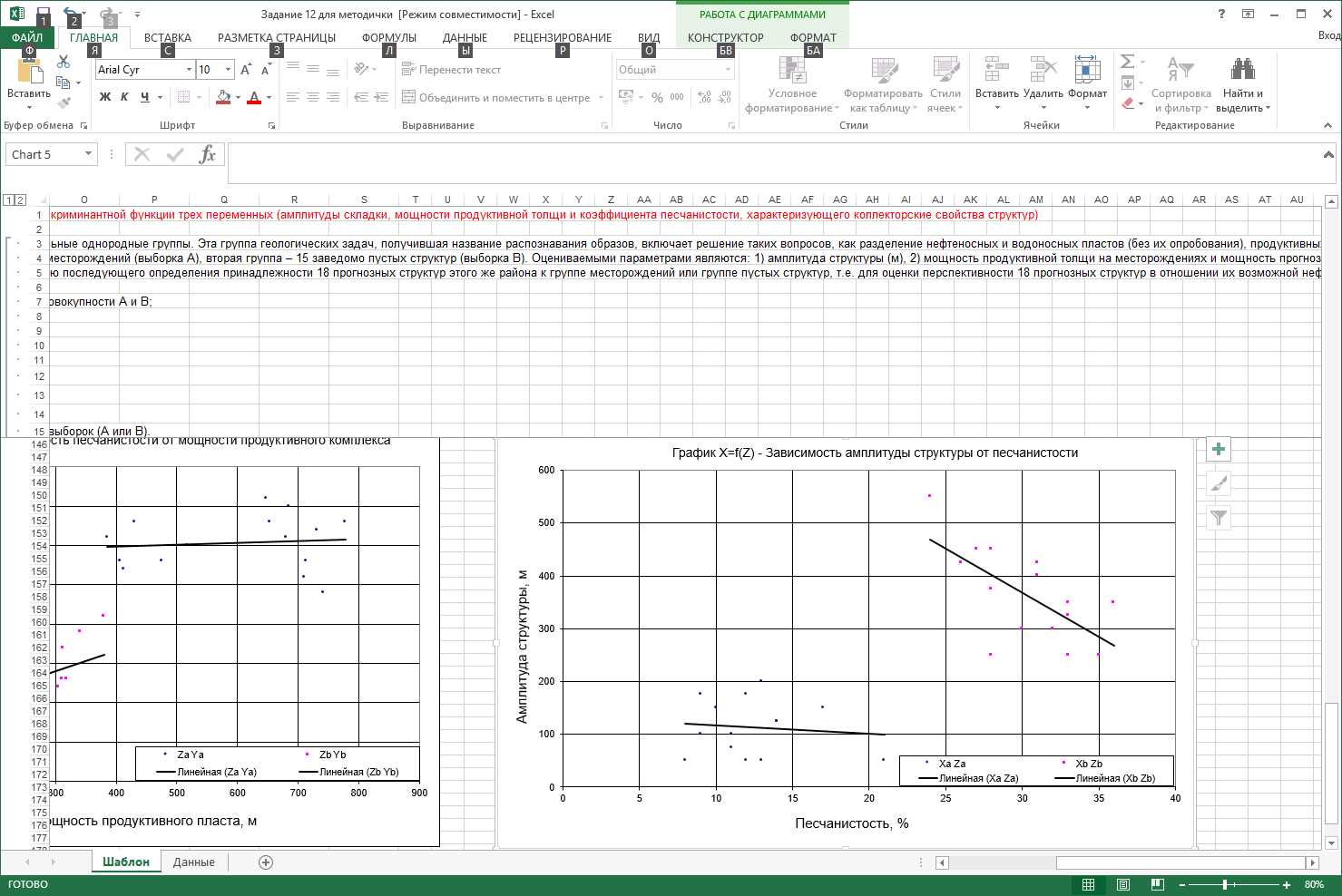 рассчитать ковариации и составить основную ковариационную матрицу трех переменных X, Y и Z для вычисления основной детерминанты (определителя матрицы) Δ - Дельта; Для этого в таблице 1: 2.1 рассчитайте суммы квадратов отклонений исходных значений от своих средних по каждой выборке А и В:
2.2 рассчитайте суммы произведений отклонений исходных значений от своих средних по каждой выборке А и В: сумма ((ХiA – ср.ХА)*(YiA – ср.YA)); сумма ((ХiA – ср.ХА)*(ZiA – ср.ZA)); сумма ((YiA – ср.YA)*(ZiA – ср.ZA)); сумма ((XiB – ср.XB)*(YiB – ср.YB)); сумма ((XiB – ср.XB)*(ZiB – ср.ZB)); сумма ((YiB – ср.YB)*(ZiB – ср.ZB))   2.3 далее рассчитайте ковариации и заполните матрицу ковариаций:
Для нашего вариант получим следующие значения:
рассчитать детерминанты (основную - Δ и три дополнительных – Δ1, Δ2, Δ3) через вспомогательные ковариационные матрицы. Для этого: 3.1 рассчитайте разности средних значений между выборками d1, d2, d3. d1 = ср.XA - ср.XB d2 = ср.YA - ср.YB d3 = ср.ZA - ср.ZB 3.2 рассчитайте основную детерминанту Дельта [Δ] в ячейке D55: Δ = МОПРЕД(B51:D53) 3.3 рассчитайте дополнительные детерминанты - Δ1, Δ2, Δ3, через вспомогательные матрицы сформированные из основной ковариационной матрицы. Чтобы рассчитать дополнительные детерминанты необходимо составить 3 вспомогательных матрицы ковариаций (строки 59-62) из общей ковариационной матрицы, путем поочередной замены столбцов на разности средних значений признака между выборками. Сначала столбца X, затем Y, затем Z.           рассчитайте дополнительные детерминанты - Δ1, Δ2, Δ3, через функцию – “МОПРЕД” по аналогии с основной детерминантой. 3.4 рассчитайте коэффициенты a1, а2, а3: а1 = Δ1 / Δ; а2 = Δ2 / Δ; а3 = Δ3 / Δ Записать дискриминантную функцию функцию D и рассчитать дискриминантный индекс D0: D = a1X+a2Y+a3Z D0 = ( а1*(ср.XA+ср.XB)+а2*(ср.YA+ср.YB)+а3*(ср.ZA+ ср.ZB))/2 Оценить значимость линейной дискриминантной функции с помощью F-критерия Фишера и критерия Махалонобиса DM. DM = а1*d1 + а2*d2 + а3*d3  Если FрасчFтеордля принятого уровня значимости а=0,05 и при степенях свободы f1=3, f2=26, то нулевая гипотеза о равенстве двух многомерных средних (т.е. о равенстве нулю расстояния DM между ними) отвергается, т.е. дискриминантная функция признается статистически значимой. В нашей работе Fтеор=2,98 Оценить вклад каждой переменной в расстояние DM между трехмерными средними двух выборок А и В: Вклад переменной Х EX = а1*d1*100/DM Вклад переменной Y EY = а2*d2*100/DM Вклад переменной Z EZ = а3*d3*100/DM Pазделить прознозные структуры на пустые и нефтеносные путем сравнения дискриминантного индекса и расчетных значений дискриминантной функции. Принадлежность любого классифицируемого трехмерного наблюдения к одной из двух анализируемых выборок (А или В) можно определить путем подстановки его значений X, Y и Z в неравенство a1*Xi + a2*Yi+а3*Zi >= D0 Если неравенство выполняется, то единичное наблюдение следует отнести к первой совокупности, т.е. к выборке А, иначе – к выборке В. | ||||||||||||||||||||||||||||||||||||||||