Преобразование в звезду. Преобразованием треугольника в эквивалентную звезду. Преобразованием треугольника в эквивалентную звезду

• Название: Преобразованием треугольника в эквивалентную звезду
• Анкор: Преобразование в звезду
• Дата: 12.05.2022
• Размер: 32.03 Kb.
• Имя файла: Преобразованием треугольника в эквивалентную звезду.docx
• Тип: Документы; #523967

Преобразованием треугольника в эквивалентную звезду называется такая замена части цепи, соединенной по схеме треугольником, цепью, соединенной по схеме звезды, при которой токи и напряжения в остальной части цепи сохраняются неизменными.



 

[Рис.1]

Из рисунка 1 мы видим,что:

R₁₂; R₂₃; R₃₁- сопротивления сторон треугольника;

R₁; R₂; R₃- сопротивления лучей звезды;

I₁₂; I₂₃; I₃₁- токи в ветвях треугольника;

I₁; I₂; I₃- токи, подходящие к зажимам 1, 2, 3.

Выразим токи в ветвях треугольника через подходящие токи I₁, I₂, I₃.

По второму закону Кирхгофа сумма падений напряжений в контуре треугольника равна нулю:

I₁₂R₁₂+I₂₃R₂₃+I₃₁R₃₁=0

По первому закону Кирхгофа для узлов 1 и 2

I₃₁=I₁₂-I₁; I₂₃=I₁₂+I₂

При решении этих уравнений относительно I₁₂ получим: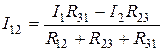



Напряжение между точками 1 и 2 схемы треугольника:



Напряжение между этими же точками схемы звезды равно:

U₁₂=I₁R₁-I₂R₂.

Т.к. речь идет об эквивалентном преобразовании, то необходимо равенство напряжений между данными точками двух схем, т.е.



Это возможно при условии: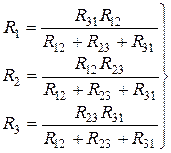

   (25)



Исходя из выражения (25) формулируется следующее правило:

Выше было получено выражение для тока в стороне 1-2 треугольника в зависимости от токов I₁ и I₂. Круговой заменой индексов можно получить токи в двух других сторонах треугольника: