Как изменится дебит скважины при увеличении ее радиуса вдвое, если фильтрация происходит по закону Дарси. Даны начальный радиус. малкин. Приемы формирования умения решения задач на движение
 Скачать 180.68 Kb. Скачать 180.68 Kb.
|
|
Приемы формирования умения решения задач на движение В школьном курсе математики широко применяются несколько способов решения текстовых задач: - арифметический способ; - алгебраический способ; - способ подбора; - графический способ; - практический способ. Все способы равноправны, но наиболее универсальными являются алгебраический и арифметический. Педагоги за период своей работы в школе сталкиваются с тем, что текстовые задачи не всегда понимаемы учениками, поэтому каждый старается помочь ребенку, применяя новые приемы и способы решения текстовых задач. В Таблице 1 рассмотрены способы решения текстовых задач разными педагогами. Таблица 1 Способы решения текстовых задач
Для обучения методике решения текстовых задач по математике в начальной школе педагогу необходимо использовать различные приемы обучения, которые бы соответствовали развитию логического мышления и творческих способностей детей. Учащихся следует знакомить с различными методами решения текстовых задач: арифметическим, алгебраическим, геометрическим, логическим и практическим; с различными видами математических моделей, лежащих в основе каждого метода; а также с различными способами решения в рамках выбранного метода. Решение текстовых задач дает богатый материал для развития и воспитания учащихся. Краткие записи условий текстовых задач – примеры моделей, используемых в начальном курсе математики. Метод математического моделирования позволяет научить школьников: а) анализу (на этапе восприятия задачи и выбора пути реализации решения); б) установлению взаимосвязей между объектами задачи, построению наиболее целесообразной схемы решения; в) интерпретации полученного решения для исходной задачи; г) составлению задач по готовым моделям и др. Математика – это орудие для размышления, в ее арсенале имеется большое количество задач, которые на протяжении тысячелетий способствовали формированию мышления людей, умению решать нестандартные задачи, с честью выходить из затруднительных положений. К тому же воспитание интереса младших школьников к математике, развитие их математических способностей невозможно без использования в учебном процессе задач на сообразительность, задач-шуток, математических фокусов, числовых головоломок, арифметических ребусов и лабиринтов, дидактических игр, стихов, задач-сказок, загадок и т.п. Основной метод решения текстовых задач в начальной школе – арифметический. Большинство действующих программ для начальной школы не ставят своей целью формирование у школьников умений решать текстовые задачи геометрическим методом, хотя он широко используется для построения вспомогательных моделей в ходе решения задач различных видов. В последнее время арсенал учителя начальных классов пополнился учебниками математики, в которых предусмотрено ознакомление учащихся с этим методом решения задач. Так, в учебниках Л.Г. Петерсон приводятся задачи «на движение», решение которых осуществляется с использованием либо конструктивного приема, либо графико-вычислительного – основными приемами геометрического метода решения текстовых задач. Использование геометрического метода в курсе начальной школы позволяет разнообразить работу по решению задач, способствует ознакомлению учащихся с методом математического моделирования, развивает логическое мышление и познавательный интерес детей. Подробно с этим методом решения текстовых задач и его применениями можно познакомиться в работах, которые приведены в конце статьи. Приведем подборку задач, которые, на наш взгляд, расширяют границы применения геометрического метода в начальной школе и являются дополнением к системе задач, предложенных в некоторых федеральных комплектах учебников математики для начальных классов. К тому же эти задания может использовать учитель, работающий по любой системе обучения, на внеклассных занятиях. В каждом примере приводится возможный вариант беседы учителя с классом. Пример 1. Ознакомление учащихся с построением графика движения. Задача. Петя вышел из города A по шоссе со скоростью 4 км/ч. На каком расстоянии от города A будет мальчик через 5 часов? – Покажите движение мальчика с помощью числового луча (рис. 1) 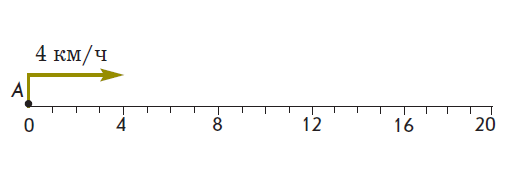 Рис. 1 – На каком расстоянии от города A Петя будет через 5 часов с момента его выхода? (20 км.) – Какую величину мы откладывали на числовом луче при решении задач на движение? (Расстояние.) – А как вы узнали, на каком расстоянии от пункта A будет находиться мальчик через 5 часов? (4 · 5 = 20.) – Сегодня мы познакомимся с другим методом решения таких задач на движение. Построим горизонтальную прямую. Отметим на ней начало координат – точку О, как в предыдущем случае. Назовем ее ось Ox. На ней будем откладывать время движения мальчика. Выберем единичный отрезок, равный 1 часу. Чтобы отразить на чертеже зависимость между временем и расстоянием, нам понадобится еще и вертикальная ось. Проведем через точку О вертикальную ось. Назовем ее ось Oy. На ней будем откладывать расстояние, пройденное мальчиком. Выберем единичный отрезок, равный 1 км. Начало движения Пети обозначим точкой A(0; 0). 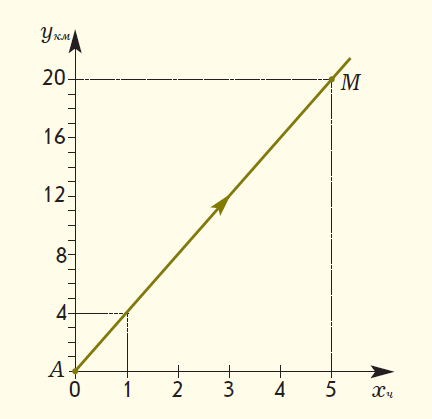 Рис. 2 – Что известно в задаче о движении мальчика? (Он вышел из города A со скоростью 4 км/ч.) – Поясните, как вы понимаете фразу «вышел со скоростью 4 км/ч». (За 1 час мальчик проходит 4 км.) – Покажите на оси времени (оси Ox) точку, координата которой 1 ч. – А теперь на оси расстояния (оси Oy) покажите точку, координата которой 4 км. – Точка (1; 4) показывает, что Петя за 1 час прошел 4 км. Отметим ее. – Мальчик движется по прямой. Через найденную нами точку и точку, показывающую начало его движения, проведем прямую. Это и есть график движения мальчика (рис. 2). – Попробуйте теперь самостоятельно ответить на вопрос задачи. Найдите точку на графике, которая поможет определить, на каком расстоянии от города А будет находиться мальчик через 5 часов после начала его движения. (Точка M.) – Можно ли по графику узнать, за какое время Петя пройдет 8 км, 12 км и т.д.? Пример 2. Ознакомление учащихся с построением графика движения объекта, скорость которого изменяется в процессе движения. Задача. Из пункта А в пункт В вышел пешеход. Первые 2 часа он шел со скоростью 4 км/ч, затем один час со скоростью 2 км/ч и оставшиеся 3 часа – со скоростью 6 км/ч. Найти расстояние между пунктами А и В. На каком расстоянии от пункта А пешеход был через 6 часов? – Отметим точку А(0; 0). Построим график движения пешехода за первые 2 часа его движения. (За 1 час он про2 шел 4 км, за 2 часа – 8 км.) Отметим точку С(2; 8) и соединим ее с точкой А (рис. 3). 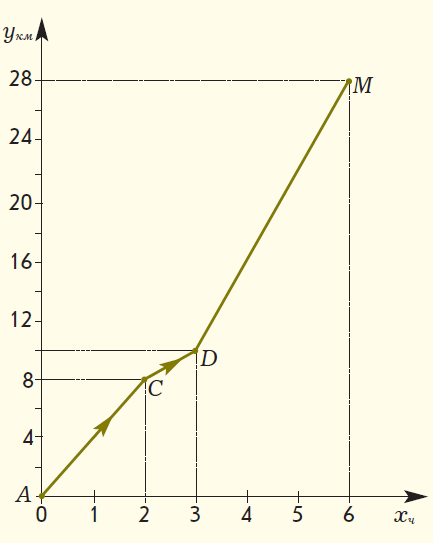 Рис. 3 – Что известно о дальнейшем движении пешехода? (Следующий час он шел со скоростью 2 км/ч.) – Построим график движения пешехода в следующий час его движения. Из какой точки будем продолжать строить этот график? (Из точки С.) – Почему из точки С? (Пешеход продолжает двигаться, только с другой скоростью.) – За следующий час пешеход пройдет 2 км, значит, он будет находиться от точки А на расстоянии 10 км (8 км + 2 км). К этому времени он будет находиться в пути 3 часа. Отметим точку (3; 10). Обозначим эту точку буквой D(3; 10). Соединим точки С и D. – Пешеход шел еще 3 часа со скоростью 6 км/ч. Построим график движения пешехода за это время. – За 1 час пешеход прошел еще 6 км, за 3 часа – 18 км, т.е. он будет находиться от точки А на расстоянии 28 км (10 км + 18 км). К этому времени он будет находиться в пути 6 часов. Отметим точку М(6; 28). Следовательно, расстояние между пунктами A и B равно 28 км. Пример 3. Решение задач на встречное движение с одновременным выходом. Задача. Отец выехал из села в город на автобусе, одновременно навстречу ему из города в село на велосипеде выехал сын. Между городом и селом расстояние 300 км. На каком расстоянии от села и через какое время произойдет их встреча, если скорость автобуса 60 км/ч, а велосипедиста 15 км/ч? На доске построен график (рис. 4а). – Что изображено на графике? (Движение автобуса.) – Почему? (На графике показано, что за 1 час пройдено расстояние 60 км, т.е. скорость движения – 60 км/ч, а это скорость автобуса.) – Что обозначает точка A? (Начальный пункт, из которого выехал отец, – село.) – Построим график движения велосипедиста. – Что нам известно о движении велосипедиста? (Он ехал в село из города, т.е. навстречу отцу; его скорость – 15 км/ч.) – Из какой точки будем строить график его движения? (Из точки В.) 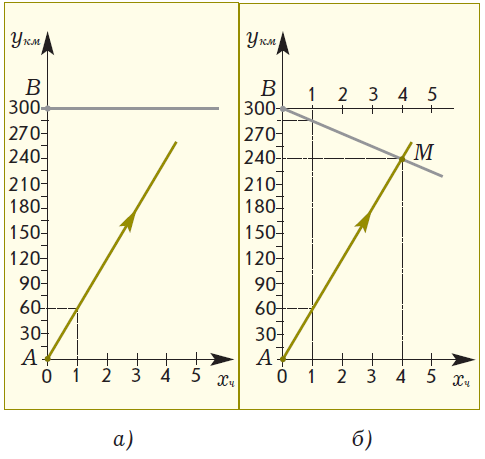 Рис. 4 – Почему? (Велосипедист и автобус движутся навстречу друг другу; выехали они в одно и то же время, значит, точка, из которой мы начнем строить график движения велосипедиста, лежит на одной вертикальной прямой с точкой А; расстояние между городом и селом 300 км, ищем точку (0; 300) – это точка В.) – Что еще необходимо учитывать при построении графика движения? (Скорость движения.) – Какова же скорость движения велосипедиста? (15 км/ч.) – А зачем нам нужна скорость движения? (Для того, чтобы определить расстояние, которое проехал сын за 1 час, – 15 км.) – Итак, спустя 1 час велосипедист находился на расстоянии 15 км от точки В, т.е. на расстоянии 285 км от точки А. Отмечаем на графике точку (1; 285) и проводим прямую через эту точку и точку В(0; 300). Тем самым мы построим график движения сына на велосипеде. Точка пересечения обоих графиков движения – место встречи отца и сына. Обозначим ее буквой М. – Чтобы узнать, на каком расстоянии от А и через какое время произошла встреча, проведем из точки М прямые под прямым углом к осям Ох и Оу. Видим, что точка M имеет координаты (4; 240). – На каком расстоянии от села произойдет встреча отца и сына? (На расстоянии 240 км.) – Через какое время после начала движения произойдет встреча? (Встреча произойдет через 4 часа.) Пример 4. Решение задачи «на движение вдогонку». Задача. Из города А со скоростью 5 км/ч вышел Ваня. Спустя 3 часа в том же направлении из города А выехал Женя на велосипеде со скоростью 10 км/ч. Через какое время Женя догонит Ваню? 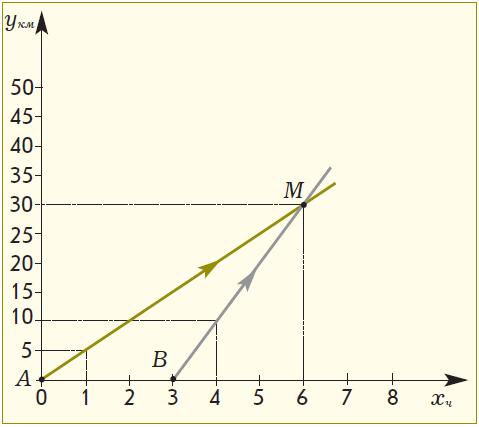 Рис.5 Рис.5– Построим график движения Вани (на графике он изображен цветной линией, рис. 5). – Построим график движения Жени. – Что нам известно о движении Жени? (Он ехал из того же города и в том же направлении со скоростью 10 км/ч.) – Из какой точки будем строить график его движения? (Из точки B (3; 0).) – Почему? (Женя выехал из города А, значит, точка, из которой мы начнем строить график его движения лежит на одной горизонтальной прямой с точкой А. Женя выехал на 3 часа позже Вани, ищем точку (3; 0) – это точка В.) – Что еще необходимо учитывать при построении графика движения? (Скорость движения.) – Какова же скорость движения Жени? (10 км/ч.) – Значит, через 1 час после начала идвижения Жени прошло 4 часа от начала движения Вани. Отмечаем на графике точку (4; 10) и проводим прямую через эту точку и точку B. – Мы построили график движения Жени. Точка пересечения графиков движения – место, в котором Женя догонит Ваню. Обозначим ее буквой М. Определяем, что точка M имеет координаты (6; 30). Следовательно, Женя догонит Ваню через 6 часов после начала движения Вани на расстоянии 30 км от города A. Пример 5. Решение задачи различными способами (с использованием графика и диаграммы). Задача. Из пункта А в пункт В выехал велосипедист со скоростью 10 км/ч. Одновременно с ним из пункта В в пункт А вышел пешеход со скоростью 5 км/ч. Через какое время произойдет их встреча, если расстояние от А до В составляет 75 км? На доске дано графическое решение задачи (рис. 6). – Что изображено на доске? (Решение задачи.) – Что показывает цветная линия? (График движения велосипедиста.) – Что показывает серая линия? (График движения пешехода.) – Почему серая линия выходит из точки В? (Пешеход и велосипедист движутся навстречу друг другу, движение начинают одновременно.) – Что означает точка М? (Момент встречи пешехода и велосипедиста.) 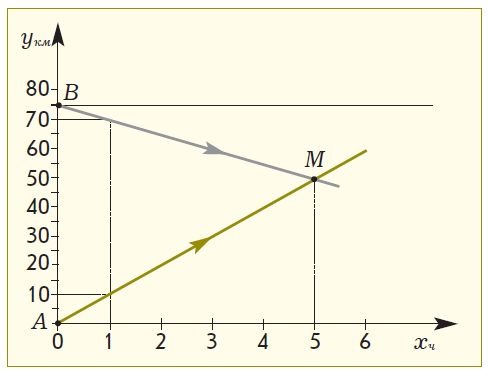 Рис. 6 – Решить эту задачу можно, построив диаграмму. Велосипедист движется из пункта А. За первый час велосипедист проехал 10 км; проведем цветной вертикальный отрезок длиной 10 км из точки (1; 0) вверх (рис. 7). Пешеход движется навстречу велосипедисту из пункта В. За первый час пешеход прошел 5 км; проведем вертикальный отрезок серого цвета длиной 5 км из точки (1; 75) вниз. Велосипедист за два часа проехал 20 км; проведем цветной вертикальный отрезок длиной 20 км из точки (2; 0) вверх. За два часа пешеход прошел 10 км; проведем вертикальный отрезок серого цвета длиной 10 км из точки (2; 75) вниз. 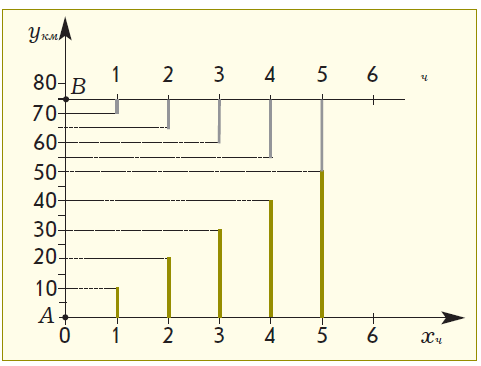 Рис.7 Велосипедист за три часа проехал 30 км; проведем цветной вертикальный отрезок длиной 30 км из точки (3; 0) вверх. За три часа пешеход прошел 15 км; проведем вертикальный отрезок серого цвета длиной 10 км из точки (3; 75) вниз. Продолжите построение диаграммы. Что вы заметили? (Цветной и серый отрезки «встретились» через 5 часов.) – Что это означает? (Пешеход и велосипедист встретились через 5 часов.) |
