МОЦТ лаба. Программа для выделения комплексов с помощью Mathcad
 Скачать 1.03 Mb. Скачать 1.03 Mb.
|
|
ВВЕДЕНИЕ Промышленные процессы протекают в сложных химико-технологи-ческих системах (ХТС), которые представляют собой совокупность аппаратов и машин, объединенных в единый производственный комплекс для выпуска продукции. В методических указаниях приводятся необходимые сведения по структурному анализу замкнутых ХТС - одному из основных этапов моделирования ХТС. Методические указания состоят из двух частей: первая часть теоретическая, вторая часть представляет собой задания для выполнения лабораторной работы. В первой главе методических указаний даются основные понятия по расчету замкнутых химико-технологических систем. Во второй главе перечисляются основные задачи структурного анализа замкнутых ХТС. Приводится программа для выделения комплексов с помощью Mathcad. В третьей главе предлагаются варианты лабораторных работ для структурного анализа замкнутых ХТС. При использовании методических указаний целесообразно сначала обратиться к вводным материалам, которые содержатся в главах 1-2, затем перейти к выполнению лабораторной работы. Авторы приносят свою благодарность Э.В. Шепелевской за помощь в подготовке рукописи методического пособия к печати. СТРУКТУРНЫЙ АНАЛИЗ ЗАМКНУТЫХ ХИМИКО-ТЕХНОЛОГИЧЕСКИХ СИСТЕМ Рассмотрим решение задачи анализа замкнутой ХТС, представленной на рисунке 1.1. 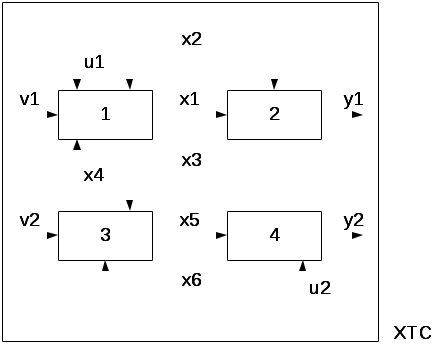 Рисунок 1.1 -Блок-схема ХТС При этом задано следующее: Топология - 4 аппарата химической технологии с известным математическим описанием в виде функциональных зависимостей:
Параметры потоков ХТС: V - вектор параметров входных потоков V=(v1,v2); X - вектор параметров промежуточных потоков X=(x1,x2,x3,x4,x5,x6); Y - вектор параметров выходных потоков, Y=(y1,y2). Управление ХТС: U - вектор управляющих воздействий U=(u1,u2). Задача анализа ХТС заключается в нахождении следующих переменных: X=(x1,x2,x3,x4,x5,x6,x7), Y=(y1,y2). Математическое описание рассматриваемой ХТС состоит из 8 уравнений с 8 неизвестными. Следует отметить, что для реальных ХТС число таких уравнений может составлять несколько тысяч. Для решения задачи анализа ХТС существует два способа. 1-й способ. Интегральный метод При небольшом количестве уравнений решать их совместно. При расчёте системы уравнений используется их структура. При этом решение существенно упрощается. 2-й способ Декомпозиционный метод Он предполагает разбиение одной сложной задачи на подзадачи. Этот метод является хорошо разработанным и широко используется в современных программных продуктах. Основная задача разбивается на следующие подзадачи: Превращение замкнутой системы в разомкнутую. Для этого замкнутая ХТС путём мысленного разрыва некоторых потоков превращается в разомкнутую. В результате на местах таких разрывов образуется по 2 потока. Определение порядка расчёта элементов для полученной разомкнутой системы. Собственно поэлементный расчёт схемы. Обеспечение равенства параметров полученных потоков. Для этого на местах разрыва потоков приходится решать дополнительные уравнения. Их количество равно суммарной параметричности разрываемых потоков. В общем случае их число равно m∙(k+2), где m - число разрываемых потоков для превращения замкнутой системы в разомкнутую, k - число веществ, функционирующих в потоках. Решение дополнительных уравнений является своеобразной платой за последовательный расчёт элементов схемы. В общем случае существует несколько вариантов превращения замкнутой ХТС в разомкнутую. Предпочтение отдают варианту, для которого на местах разрыва нужно решать меньшее число уравнений (рисунок 1.2). 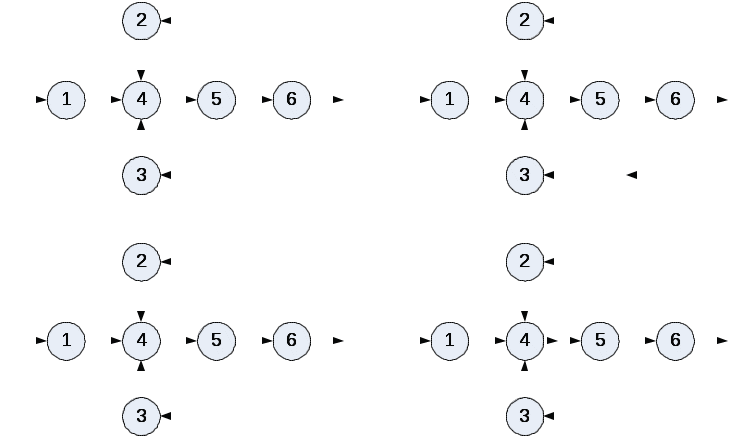 Рисунок 1.2 - Превращение замкнутой ХТС в разомкнутую ХТС На рисунке 1.2 представлена некоторая схема и три варианта превращения этой ХТС в разомкнутую ХТС. Предположим, что k=4 и пусть математическое описание каждого элемента состоит из 4 уравнений. Тогда интегральный подход состоит в решении системы из 6∙4=24 уравнений. Модульный подход предполагает последовательное решение 4 уравнения для каждого из шести элементов. Однако при этом необходимо решать на местах разрывов дополнительные уравнения. При этом два из трёх вариантов связаны с дополнительным решением на 2 -х местах разрывов 2∙(4+2)=12 уравнений (рисунок 1.2). В то время как последний вариант разрыва (рисунок 1.2) предполагает дополнительное решение 1∙(2+4)=6 уравнений. Принято, что решение 6 уравнений проще, чем 12, и, поэтому предпочтение отдается именно этому варианту разрыва. 2 ОСНОВНЫЕ ЗАДАЧИ СТРУКТУРНОГО АНАЛИЗА ЗАМКНУТЫХ ХТС При выполнении структурного анализа замкнутой ХТС решаются следующие основные задачи: Нахождение совокупности элементов ХТС, которые могут рассчитываться только совместно, т. е выделение комплексов. Составление предварительной последовательности расчета комплексов и аппаратов, не входящих в комплексы. Определение для каждого комплекса оптимального множества разрываемых дуг (потоков) и превращение каждого комплекса в разомкнутую подсистему. Определение окончательной последовательности расчета ХТС в целом. 2.1 АЛГОРИТМЫ ВЫДЕЛЕНИЯ КОМПЛЕКСОВ Алгоритмы выделения комплексов используют основное свойство вершин графа, принадлежащих комплексу. Для любых двух вершин I и J, входящих в комплекс, должен существовать путь из I-й в J-ю вершину и обратный путь из J-и в I-ю вершину (двигаясь в направлении ориентированных дуг). Для выделения комплексов существуют различные матричные алгоритмы. Некоторые из них связаны с представлением структуры ХТС в виде матрицы связей и последующими операциями с этой матрицей с целью выделения на графе ХТС путей различной длины и построения матрицы комплексов.В основе других алгоритмов лежит использование матрицы путей на графе. Матрица путей является квадратной и содержит столько столбцов, сколько элементов имеется в составе ХТС. Если на графе есть путь любой длины из вершины I в вершину J, то на пересечении I-й строки и J-го столбца матрицы путей ставится 1, иначе ставится - 0. На главной диагонали этой матрицы ставятся единицы, так как считается, что путь длиной 0 из любого элемента в этот же самый элемент всегда существует. 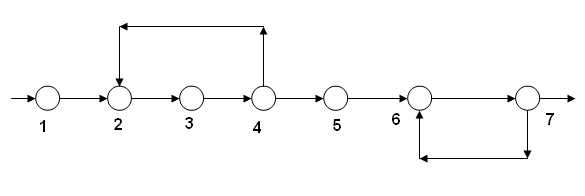 Рисунок 2.1 -Граф ХТС Матрица путей графа ХТС, представленной на рисунке 2.1 (обозначим эту матрицу буквой Р), имеет вид:
Наряду с матрицей Р. строится вспомогательная матрица S. Она является транспонированной по отношению к матрице Р, т. е. столбцы матрицы S являются строками матрицы Р:
Элементы матрицы Р указывают на наличие пути из I вершины в J-ю вершину, а элементы матрицы S - из J-й вершины в I-ю. Логически перемножая элементы матриц Р и S (полагая 0 * 0 = 0, 0 * 1 = 0, 1 * 0 = 0, 1 * 1 = 1), получим матрицу комплексов D:
С помощью матрицы D определяются комплексы, входящие в состав графа ХТС, по следующим правилам: - если в I-ой строке этой матрицы имеется только один не нулевой элемент d(I,I)=1 (принадлежащий главной диагонали), то элемент ХТС с номером I может быть рассчитан отдельно от остальных элементов системы. В рассматриваемом примере это элементы 1 и 5; - строки матрицы D, имеющие, кроме элемента d (1,1), другие не нулевые элементы, соответствуют комплексам. Не нулевые элементы строк указывают вершины графа, входящие в состав комплекса. В нашем примере, согласно матрице D, в состав ХТС входят два комплекса: комплекс 1 - (2, 3, 4) комплекс 2 - (6, 7). Одинаковые строки матрицы соответствуют одному и тому же комплексу. Для решения задач структурного анализа ХТС используют различные алгоритмы. Остановимся на одном из них. Рассмотрим три любые вершины графа ХТС: I, J, M. Если существует путь любой длины из вершины I в вершину J и из вершины J в I, то эти вершины принадлежат одному и тому же комплексу К. Для присоединения вершины M к комплексу K необходимо проанализировать, есть ли путь из любой вершины (например, I принадлежащей комплексу К, в вершину M и обратный путь из вершины M в любую вершину комплекса К (например, I). Если эти два пути существуют, то вершина M принадлежит комплексу К Применение этого правила к ХТС, изображенной на рисунке 2.2, позволяет выделить следующие комплексы: - комплекс К1- (1,2, 3, 8, 9, 10), комплекс К2 - (5,11) , элементы 4,6, 7 рассчитываются автономно. 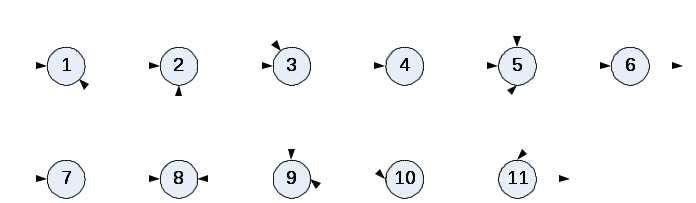 Рисунок 2.2 - Граф некоторой замкнутой ХТС 2.2 ПРОГРАММА ДЛЯ ВЫДЕЛЕНИЯ КОМПЛЕКСОВ На первом этапе работы программы формируется матрица связей, матрица заполняется 0-ми элементами, диагональные элементы приравниваются 1. Далее задаются связи графа ХТС и формируется окончательный вид матрицы связей. После возведения матрицы связей в степень n (где n –число элементов ХТС) получается матрица путей b. Наличие связей из вершины i в вершину j и связи из вершины j в i определяет элементы, входящие в комплекс (матрица к). Ниже представлены листинги программ для решения этой задачи с помощью системы компьютерной математики Mathcad.  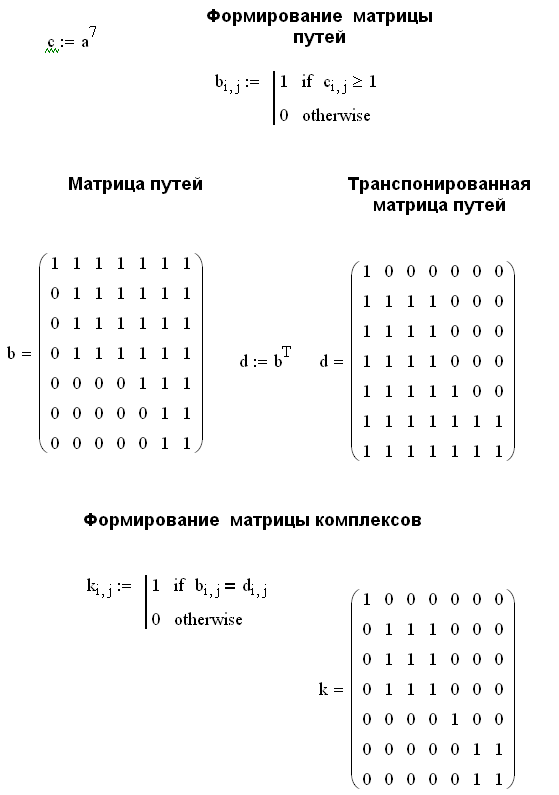 2.3 ОПРЕДЕЛЕНИЕ ПРЕДВАРИТЕЛЬНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ РАСЧЕТА ХТС После выделения комплексов определяют предварительную последовательность расчета ХТС (ППРС). Совокупность вершин, входящих в комплекс, объединяют в одну новую вершину, в результате чего получается граф, не содержащий контуров (рисунок 2. 3).  Рисунок 2.3 - Определение ППРС Такой граф соответствует разомкнутой ХТС. Поэтому определение предварительной последовательности расчета замкнутой системы (ППРС) производится по алгоритмам, применяемым в структурном анализе разомкнутых ХТС [1]. Для рассмотренной системы имеем: ППРС - [7, (1, 2. 3, 8, 9, 10), 4, (5, 11), 6] 2.4 АЛГОРИТМЫ ВЫДЕЛЕНИЯ КОНТУРОВ Выделение контуров производится отдельно для каждого комплекса. Один из способов выделения контуров заключается в построении прадерева комплекса. Прадеревом комплекса с корнем К, называют такое изображение всех путей, существующих в комплексе, при котором в каждую вершину, отличную от К, входит только одна дуга. В вершину К прадерева ни одна дуга не входит. Построение каждого пути продолжают до тех пор, пока на нем не встретятся повторяющиеся вершины. В этом случае построение соответствующего пути заканчивают, а последнюю вершину называют висячей вершиной прадерева. Выделение контуров целесообразно проводить в следующей последовательности: Представляют структуру каждого комплекса, например, в виде списка связи. В качестве примера ниже приводится список связи комплекса (1, 2, 3, 8, 9. 10), входящего в состав ХТС, представленной на рисунке 2.3.
Производят построение прадерева комплекса. Для построения прадерева из любой вершины комплекса, которую принимают за корень прадерева, строят все пути, существующие в комплексе. Каждую ветвь строят до тех пор, пока на ней не встретится уже имеющаяся вершина (висячая вершина). Участки ветвей прадерева между повторяющимися вершинами являются контурами, входящими в состав комплекса. Каждой висячей вершине соответствует контур. На рисунке 2.4 показано прадерево комплекса (1, 2, 3, 8,9, 10)(см. выше соответствующий список связи). Римскими цифрами отмечены висячие вершины прадерева. 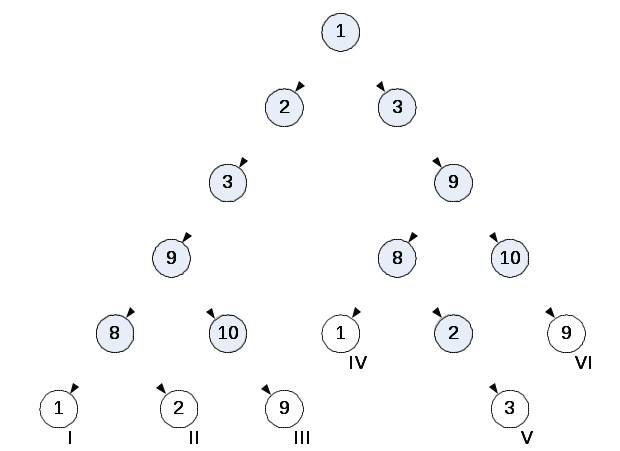 Рисунок 2.4- Выделение контуров комплекса (1, 2, 3, 8, 9, 10). Выделенные контуры заносят в таблицу контуров. В таблице 2.1 приведены контуры, входящие в состав рассматриваемого комплекса. Таблица 2.1- Контуры, входящие в состав комплекса (1, 2, 3, 8, 9,10)
Как видно из таблицы 2.1, общее число висячих вершин прадерева больше числа различных контуров, так как различные висячие вершины могут отвечать одному и тому же контуру. В рассматриваемом комплексе висячим вершинам 1 и IV соответствуют одинаковые контуры 9-10-9 и вершинам III и VI одинаковые контуры 2- 3-9-8-2 и 3- 9- 8- 2- 3.Для дальнейшей работы из двух или нескольких одинаковых контуров в таблице контуров оставляют только один. То, что одни и те же контуры выделяются иногда несколько раз, является недостатком рассмотренного алгоритма. 2.5 АЛГОРИТМЫ ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНОГО МНОЖЕСТВА РАЗРЫВАЕМЫХ ПОТОКОВ С точки зрения трудоемкости и точности расчетов небезразлично, в каких местах производить разрыв связей комплекса. Для того чтобы режим в разомкнутой ХТС соответствовал режиму в комплексе, необходимо выполнение условия равенства параметров потока после места разрыва соответствующим параметрам до места разрыва. Можно показать, что данное условие приводит к необходимости решения системы нелинейных уравнений, суммарный порядок которой равен сумме параметричностей разрываемых дуг (параметричность или размерность дуги - это число параметров, характеризующих соответствующий технологический поток). При выборе мест разрывов в качестве критерия оптимальности может использоваться суммарная параметричность разрываемых дуг, т. е. сумма неизвестных параметров потоков в местах разрыва. Для отыскания оптимально-разрывающего множества дуг строится матрица входящих в комплекс контуров, в которой группируется необходимая информация для решения рассматриваемой задачи. Элементы матрицы контуров К (I,J) (I- номер контура, J- номер дуги) определяется по следующему правилу:
Определим теперь контурную степень J-й дуги f(J): она равна числу контуров, в которые входит данная дуга, т. е. числу единиц, стоящих под дугой J. Чем больше контурная степень дуги, тем больше будет разомкнуто контуров при ее разрыве. Если f(I)= f(J), причем I-я и J-я дуги входят в одни и те же контуры, то предпочтительнее разрывать дугу с меньшей параметричностью р. В нашем примере параметричности дуг выбраны условно. Матрица контуров комплекса (1, 2, 3, 8, 9, 10) имеет вид:
При отыскании оптимального множества разрываемых дуг нужно учитывать следующие правила: 1) количество мест разрывов должно быть выбрано так, чтобы были разорваны все контуры комплекса. 2) если параметричность всех дуг одинакова, задача сводится к определению минимального числа дуг, разрыв которых превращает комплекс в разомкнутую подсистему. В этом случае следует найти дугу, имеющую максимальную контурную степень. В нашем примере максимальное значение f имеет дуга 3-9 или 9-8. Разрыв любой из этих дуг приведет к уменьшению числа контуров в комплексе (у нас контуры К2, КЗ и К4 окажутся разомкнутыми). Из матрицы контуров вычеркнем эти контуры и вновь пересчитаем контурные степени оставшихся дуг. Вновь разыскиваем среди этих дуг дугу, имеющую максимальную контурную степень, и исключаем соответствующие контуры. Этот процесс продолжают до тех пор, пока не останется контуров. В нашем примере все контуры могут быть разомкнуты после разрыва двух дуг 3-9 и 9-10 или 9-8 и 10-9, что свидетельствует о том, что решение задачи может быть не единственным. 3) В общем случае, когда параметричность дуг комплекса различна, разрываемые дуги выбираются так, чтобы их суммарная параметричность была минимальной. Для определения наиболее выгодных мест разрыва в этом случае необходимо найти всевозможные варианты разрываемых дуг (с учетом правила 1), определить суммарные параметричности различных вариантов и найти среди этих параметричностей минимальную. Множество разрываемых дуг с минимальной суммарной параметричностью и будет оптимальным. Для рассматриваемого примера в таблице 2.2 представлены различные варианты множеств разрываемых дуг. Как видно из таблицы, минимальную суммарную параметричность имеет множество дуг (2-3, 8-1, 9-10). Именно эти дуги следует разрывать для превращения комплекса в разомкнутую ХТС в рассматриваемом примере. Таблица 2. 2 - Варианты множеств разрываемых дуг комплекса (1,2,3,8,9,10)
ОПРЕДЕЛЕНИЕ ОКОНЧАТЕЛЬНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ РАСЧЕТА ХТС После разрыва дуг, входящих в оптимальное множество разрываемых дуг, каждый комплекс превращается в разомкнутую подсистему, а вся ХТС в целом - в разомкнутую систему. Для каждого разомкнутого комплекса с помощью алгоритмов определения вычислительной последовательности разомкнутых систем легко определить порядок расчета входящих в него элементов. Так, для комплекса (1, 2, 3, 8, 9, 10) вычислительная последовательность расчета имеет вид (1,3, 10, 9, 8, 2). Для решения дополнительных уравнений на местах разрыва в программах расчета ХТС используются так называемые фиктивные итерационные блоки. Предполагается, что в этих блоках задаются начальные приближения значении параметров разорванных потоков и сводятся к минимуму рассогласования значений параметров разорванных потоков. Способ включения итерационного блока (ИБ) в информационную схему расчета ХТС показан на рисунке 2.6. Последовательность расчета комплекса (1,2,3,8,9, 10) такова: в итерационном блоке 1 (на выходе) задаются начальные приближения для параметров разорванных потоков 2-3, 8-1, 9-10. После этого, по известным математическим описаниям элементов в определенной последовательности вычисляются выходные параметры аппаратов 1, 3, 10. 9, 8, 2. В результате расчета на входе итерационного блока получаются последующие приближения для параметров соответствующих разорванных потоков. Если разность значений параметров потоков на входе и выходе итерационного блока больше заданной точности, то задается новое приближение и поиск решения продолжается. Таким образом, последовательность расчета рассматриваемого комплекса имеет вид: (ИБ1 ,1,3,10,9,8,2). Последовательность расчета комплекса (5, 11) не нуждается в пояснении. Полученные последовательности расчета отдельных комплексов подставляют в предварительную последовательность и получают окончательную последовательность расчета Х'ТС. В нашем примере окончательная последовательность расчета ХТС (рисунок 2.2) имеет вид [ 7, (ИБ1, 1, 3, 10, 9, 8, 2), 4, (ИБ2, 5, 11), 6] 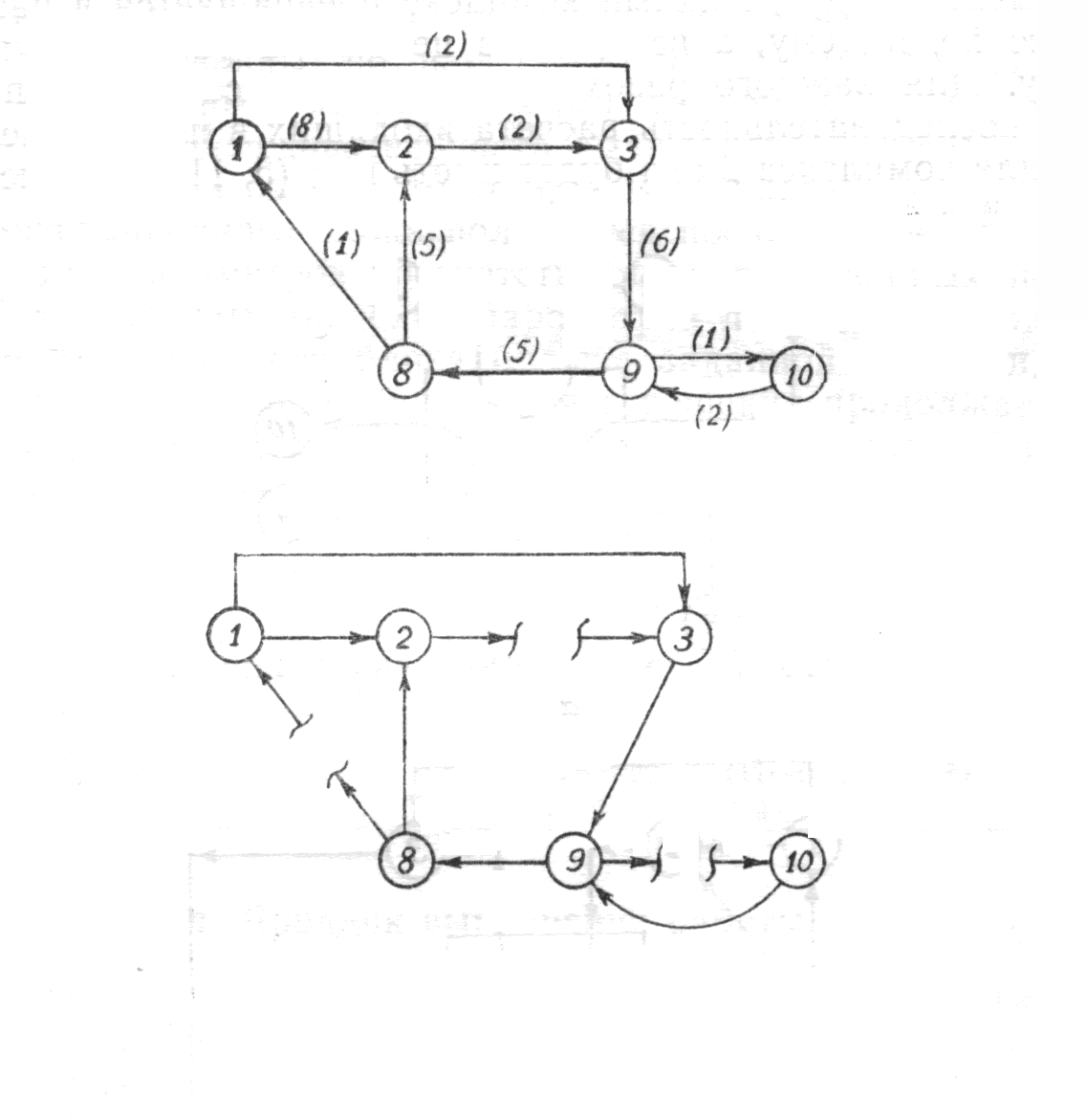 Рисунок 2.5 - Комплекс с дугами разной параметричности и соответствующая ему разомкнутая ХТС 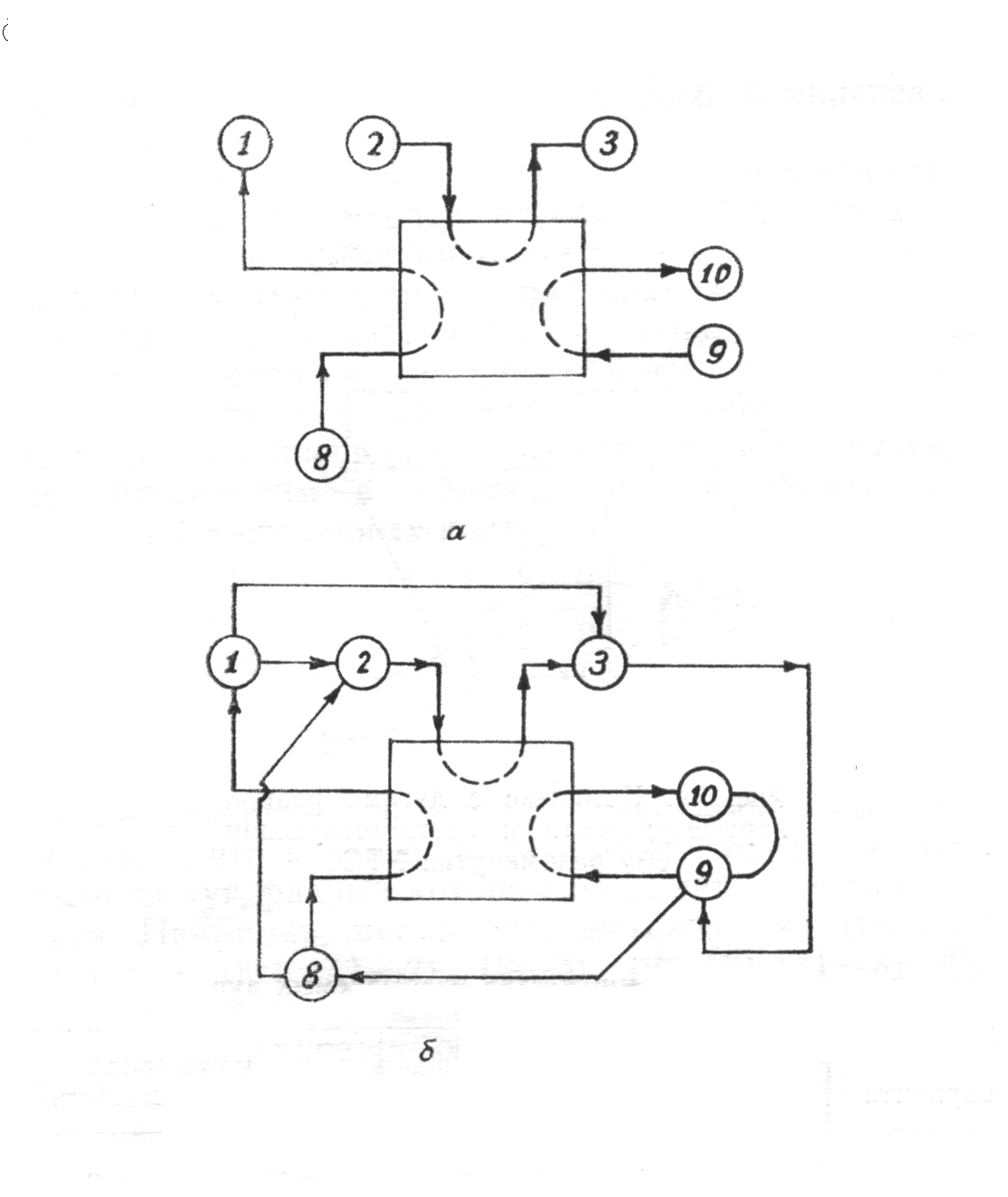 Рисунок 2.6- Информационная блок-схема расчета комплекса 1: на 1-ом (а) и 2-ом (б) этапах 3 ЛАБОРАТОРНАЯ РАБОТА №2. СТРУКТУРНЫЙ АНАЛИЗ ЗАМКНУТЫХ ХТС Для приведенных ниже вариантов индивидуальных заданий выполнить структурный анализ. В заданиях принято, что параметричность потоков равна 1.Для тех потоков, для которых она отлична от 1 ,сверху над потоком указана его параметричность. Порядок выполнения работы В соответствии с индивидуальным заданием необходимо выполнить следующее: 1. Провести структурный анализ заданной ХТС. 2. Составить информационную блок-схему расчета ХТС. Содержание отчета Отчет по лабораторной работе должен содержать: 1. Постановку задачи. 2. Результаты структурного анализа ХТС. 3. Информационную блок-схему расчета ХТС. 4. Анализ полученных результатов. Контрольные вопросы 1. Назовите способы представления структуры ХТС. 2. Сформулируйте и поясните постановку задачи расчета замкнутых ХТС. 3. Поясните метод расчета замкнутых ХТС. 4. Назовите основные задачи структурного анализа замкнутых ХТС. 5. Дайте определение пути комплекса, контура на графе ХТС. 6. Назовите виды графов ХТС. 7. Поясните алгоритмы выделения комплексов. 8. Как определяются контуры на графе ХТС? 9. Как определяется множество разрываемых дуг? 10. Поясните смысл информационной блок-схемы расчета ХТС. 3.1 ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ К ЛАБОРАТОРНОЙ РАБОТЕ №2 Задание 1 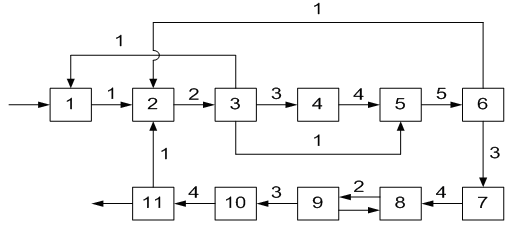 Задание 2 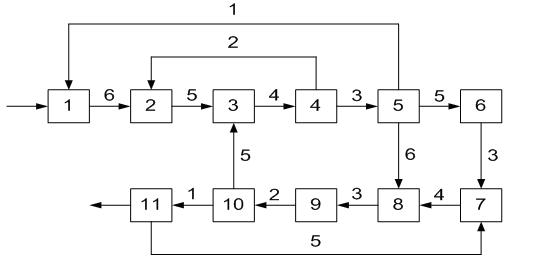 Задание 3 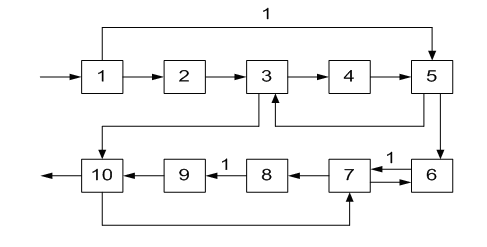 Задание 4 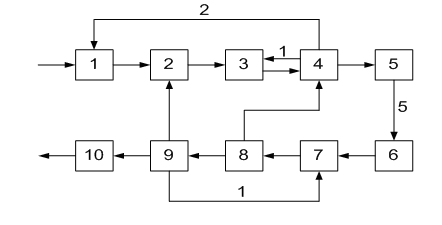 Задание 5 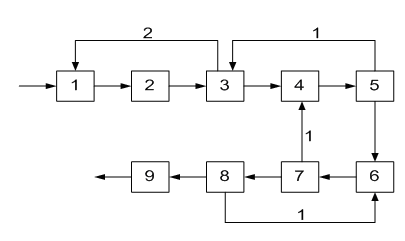 Задание 6 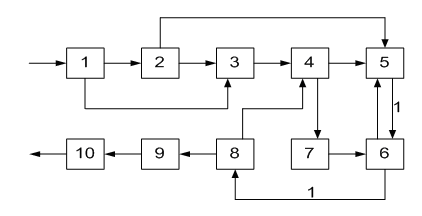 Задание 7 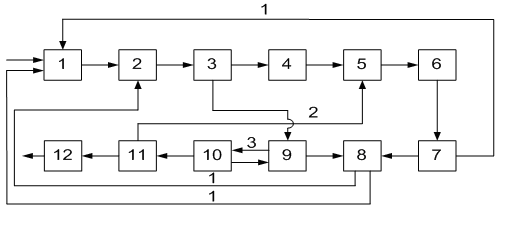 Задание 8 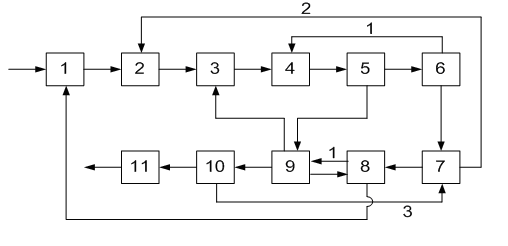 Задание 9 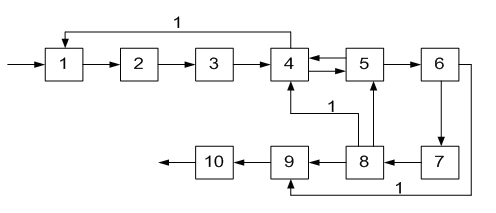 Задание 10 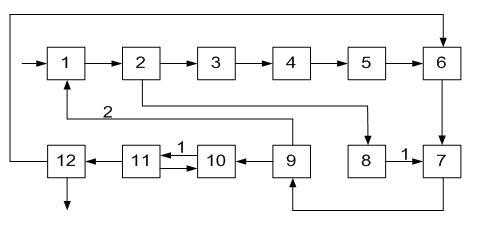 Задание 11 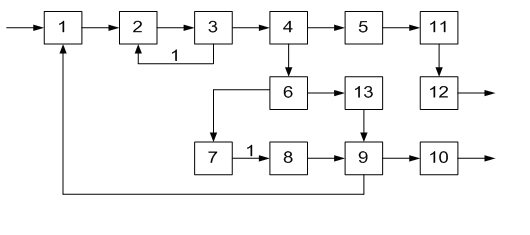 Задание 12 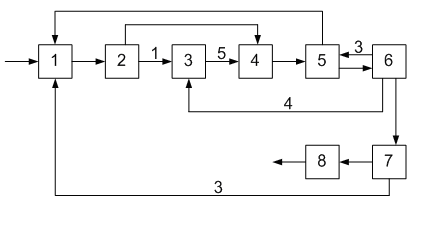 Задание 13 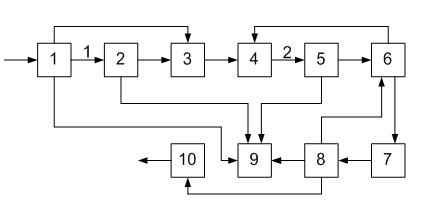 Задание 14 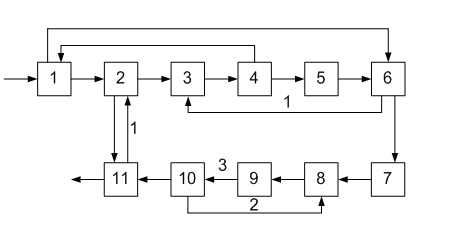 Задание 15 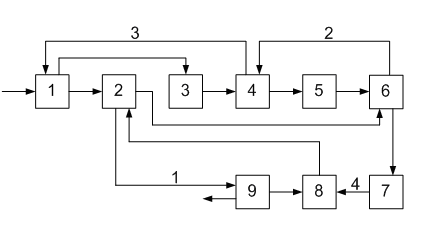 Задание 16 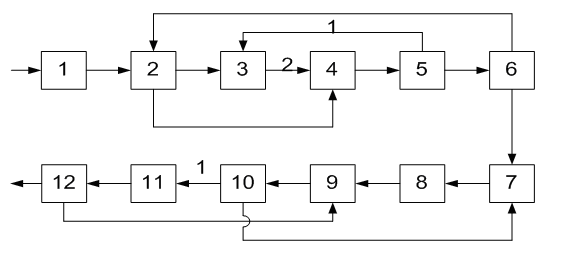 Задание 17 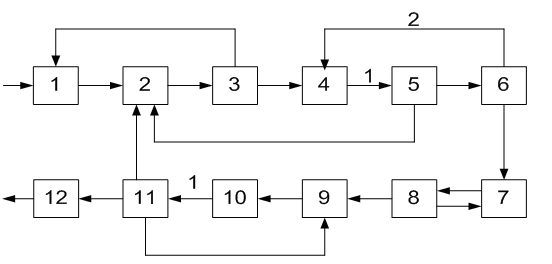 Задание 18 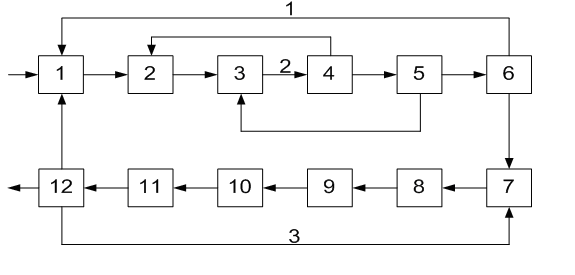 Л 13. 14. 8. 9. 10. ИТЕРАТУРА Холоднов В.А., Хартманн К, Чепикова В.Н., Андреева В.П. Системный анализ и принятие решений. Компьютерные технологии моделирования химико-технологических систем. СПб.: СПГТИ (ТУ), 2008.-160 с. Холоднов В.А, Решетиловский В.П., Лебедева М.Ю., Боровинская Е.С. Системный анализ и принятие решений. Математическое моделирование и оптимизация объектов химической технологии в Mathcad и Excel . СПб.: СПГТИ (ТУ), 2007.-433 с. СОДЕРЖАНИЕ
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
