|
|
Проэкт история. Проэкт Т.М.. Пространственная система сил
Пространственная система сил
Силы, сходящиеся в точке. Силы, линии действия которых НС лежат в одной плоскости, образуют пространственную систему сил. Если линии действия сил пересекаются в одной точке, но не лежат в одной плоскости (рис. 1.59), то они образуют пространственную систему сходящихся сил. Главный момент такой системы сил относительно точки О, в которой пересекаются линии действия сил, всегда равен нулю, т.е. такая система сил в общем случае эквивалентна равнодействующей, линия действия которой проходит через точку О.

Рис. 1.59. Пространственная система сходящихся сил
При использовании ОЗС (1.5) условия равновесия такой системы сил в рассматриваемом случае сводятся к выражению /? = (), и их можно записать в виде трех уравнений равновесия:
(1.25)
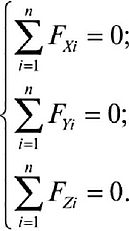
Если пространственная система сходящихся сил находится в равновесии, то суммы проекций всех сил на три декартовых оси координат равны нулю.
В случае пространственной системы сил может получиться так, что линия действия силы и ось являются скрещивающимися прямыми. В этом случае при составлении уравнений равновесия используется прием двойного проектирования (рис. 1.60).

Рис. 1.Б0. К приему двойного проектирования сил
Суть этого приема состоит в том, что для нахождения проекции силы на ось сначала проектируем ее на плоскость, содержащую эту ось, а затем уже непосредственно на саму ось: ЁХУ = Я^пу; Ех = |Т^гк|с05ф = /г5туС08ф.
Произвольная пространственная система сил. Силы, линии действия которых не лежат в одной плоскости и не пересекаются в одной точке, образуют произвольную пространственную систему сил (рис. 1.61). Для такой системы отсутствует какая-либо предварительная информация о величинах, или направлениях главного вектора и главного момента. Поэтому необходимые условия равновесия, вытекающие из ОЗС, Я = 0; М0 = 0, приводят к шести скалярным уравнениям:
с
о
II
|
Мох = 0;
|
|
II
о
|
М0У = 0;
|
(1.26)
|
Я7 —0,
|
Мо? = 0.
|
|
Из ОЗС следует, что при равновесии произвольной пространственной системы сил три проекции главного вектора и три проекции главного момента внешних сил равны нулю.
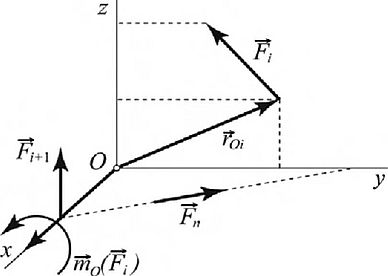
Рис. 1.61. Произвольная пространственная система сил
Практическое использование этих соотношений не вызывает труда в случае нахождения проекций сил, требуемых для вычисления проекции главного вектора, тогда как вычисление проекций векторов моментов может оказаться весьма затруднительным, так как ни величины, ни направления этих векторов заранее не известны. Решение задач значительно упрощается, если использовать понятие «момент силы относительно оси».
Момент силы относительно оси — это проекция на эту ось вектора-момента силы относительно любой точки, лежащей на этой оси (рис. 1.62):
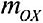
созос.
(1.27)
где /л0(/7) = г0 х Т7 — вектор-момент силы относительно точки О.
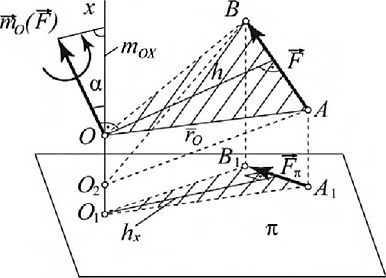
Рис. 1.Б2. К определению момента силы относительно оси
Модуль этого вектора равен |ал0(/;)| = 25ДО/1й = /7?, где — площадь треугольника ОЛВ.
минуя определение вектора-момента т0(Р). Построим плоскость л, перпендикулярную оси, относительно которой определяется момент, и спроектируем силу на эту плоскость. По определению момент силы относительно оси:
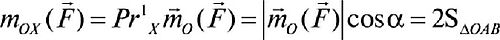
с об ос — 28ДО/)й АО, А1 В] — РКИХ.
Таким образом, модуль момента силы относительно оси можно определить как произведение модуля проекции силы на плоскость л, перпендикулярную рассматриваемой оси, на расстояние от точки пересечения оси с плоскостью л до линии действия силы Рк, т.е. для определения момента силы относительно оси нет необходимости предварительно определять вектор та(Р), а затем проектировать его на ось Ох.
Примечание. Заметим, что модуль момента относительно оси не зависит от выбора точки на оси, относительно которой вычисляют вектор момента, так как проекция площади АОАВ на плоскасть л не зависит от выбора точки О.
Из изложенного вытекает последовательность действий при определении момента силы относительно оси (см. рис. 1.61):
• строим плоскость л, перпендикулярную Ох, и отмечаем точку О;
• проектируем силу на эту плоскость;
• вычисляем модуль момента относительно оси и присваиваем полученному результату знак «+» или «—»:
(1.28)
тох(Р) = ±РЬх.
Правило знаков следует из знака проекции вектора тох(Р): если смотреть с «положительного конца» оси «поворот отрезка Их » силой Рп виден происходящим против хода часовой стрелки, то момент силы относительно оси считают положительным, в противном случае — отрицательным (рис. 1.63).
х
Р
 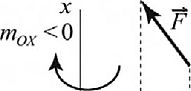 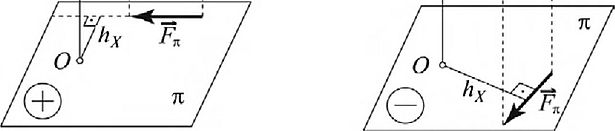
Рис. 1.63. К определению знака момента силы относительно оси
1 Рг — от фр. ргсуесйоп — проекция.
Примечание. Момент силы относительно оси равен нулю, когда сила параллельна оси или пересекает эту ось, т.е. момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости (рис. 1.64).
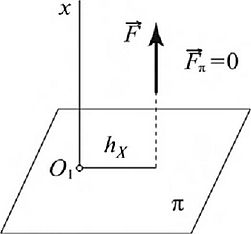 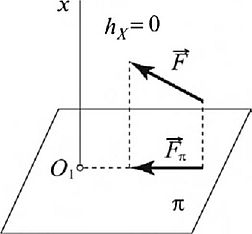
Рис. 1.В4. Случаи равенства нулю момента силы
относительно оси
С физической точки зрения момент силы относительно оси характеризует вращательный эффект силы по отношению к оси.
Уравнения равновесия произвольной пространственной системы сил. Учитывая, что согласно ОЗС для пространственной системы сил, находящейся в равновесии, Я = 0; Ма = 0. Выражая проекции главного вектора через суммы проекций сил системы, а проекции главного момента — через суммы моментов отдельных сил относительно осей, получаем шесть уравнений равновесия произвольной пространственной системы сил:
1 г» = 0.
|
п
^ тОХ
|
|
1=1
|
/=1
|
|
X Ру, = 0.
|
п
= 0;
|
(1.29)
|
/=1
|
/=1
|
|
N1
II
о
чД
|
О
II
1
"И“
|
|
Таким образом, если произвольная пространственная система сил находится в равновесии, то сумма проекции всех сил на три оси декартовых координат и суммы моментов всех сил относительно этих осей равны нулю.
Пары сил в пространстве. В пространственной системе сил могут встречаться пары сил, расположенные в разных плоскостях, и при вычислении главного момента возникает необходимость нахождения моментов этих пар сил относительно разных точек пространства, не лежащих в плоскости пар.
Пусть силы пары расположены в точках/! и В (рис. 1.65). Тогда имеем: РА = —Рв, а по модулю РА = Рв = Р. Из рис. 1.65 следует, что гв = гл + Л В.

Рис. 1.В5. К определению вектора-момента пары сил относительно точки,
не лежащей в плоскости пары
Найдем главный момент пары сил относительно точки О:
(1.30)
= Ра х К + рв х Рв = * л х + ?в х Л =
= (гв-?л)х Рв = х Рв = ВЛх РА = т.
Поскольку положение точки О не вошло в конечный результат, отметим, что вектор-момент пары сил т не зависит от выбора мо-ментной точки О и определяется как момент одной из сил пары относительно точки приложения другой силы. Вектор-момент пары сил перпендикулярен плоскости действия пары и направлен так, чтобы с конца его видеть возможное вращение против хода часовой стрелки. Модуль вектора-момента пары сил равен произведению величины силы пары на плечо, т.е. ранее определенному значению момента пары в плоской системе сил:
т0(Р,-Р) = Рк = т. (1.31)
Вектор-момент пары сил является «свободным» вектором; его можно прикладывать в любой точке пространства, не изменяя модуля и направления, что соответствует возможности переноса пары сил в любую параллельную плоскость.
Момент пары сил относительно оси. Поскольку момент пары сил — вектор «свободный», то всегда пару сил, заданную векгором-момента,
можно расположить так, чтобы одна из сил пары (-^) пересекала заданную ось в произвольной точке О (рис. 1.66). Тогда момент
пары сил будет равен моменту силы Р относительно точки О:
т0(Р,-Р) = ОЛх Р = т.

Рис. 1.ББ. К определению момента пары сил относительно оси
Момент пары сил относительно оси определяют как проекцию на эту ось вектора-момента силы F относительно точки О, или, что то же самое, как проекцию вектора-момента пары сил m0(F,-F) на эту ось:
т х (F,-F) = tn cos ос = Ргх т. (1-32)
Некоторые примеры пространственных связей:
? сферический шарнир (рис. 1.67) позволяет осуществлять поворот вокруг точки в любом направлении. Поэтому, отбрасывая такую связь, нужно приложить силу /V, которая проходит через центр шарнира и неизвестна по величине и направлению в пространстве. Разлагая эту силу по направлениям трех координатных осей, получим три неизвестные реакции: ХА, Ya, Za;
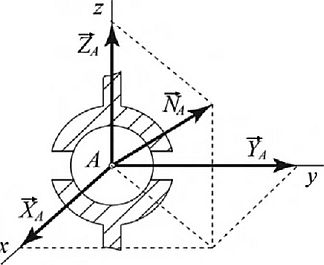  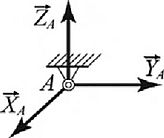
Рис. 1.Б7. Сферический шарнир и схематическое изображение его реакций
? подшипник скольжения позволяет реализовать поворот вокруг своей оси и допускает свободу перемещения вдоль этой оси. Предполагая, что размер 8 очень мал и реактивными моментами относительно осей х и у можно пренебречь, получим одну неизвестную по величине и направлению реактивную силу NА или две неизвестные реакции: ХА, УА (рис. 1.68);

Рис. 1.Б8. Реакции подшипника со свободной осью
? подпятник (рис. 1.69) в отличие от подшипника позволяет осуществлять поворот вокруг своей оси, нс допуская перемещения вдоль нее, и имеет три неизвестные реакции: XА, ?Л, Z/1;

? глухая пространственная заделка (рис. 1.70). Поскольку при отбрасывании такой связи возникает произвольная пространственная реактивная система сил, характеризуемая главным вектором /? неизвестной величины и направления и главным моментом, например, относительно центра заделки А, также неизвестным по величине и направлению, то представим каждый из этих векторов в виде компонентов по осям: Я = XА + УА + 2 А; МА = тАХ + тАУ + тАг.
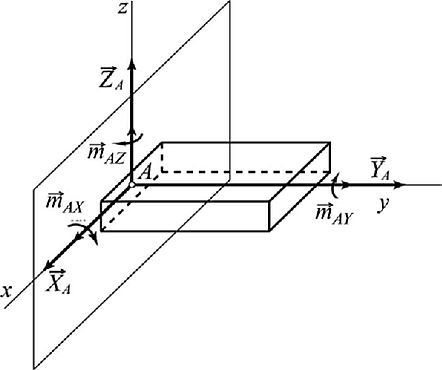
Рис. 1.70. Реакции глухой пространственной заделки
Делаем вывод, что глухая пространственная заделка имеет шесть неизвестных реакций — три составляющих силы и три момента относительно осей, величины которых равны соответствующим проекциям сил и моментов на координатные оси: XА, Ул 2А, тАХ; тАУтА/.
Решение задач. При решении задач на равновесие пространственной системы сил весьма существенным является составление уравнений, которые можно решить простым способом. Для этих целей оси, относительно которых составляют уравнения моментов, следует выбирать так, чтобы они пересекли как можно больше неизвестных сил или были им параллельны. Желательно направлять оси проекций так, чтобы отдельные неизвестные были им перпендикулярны.
При затруднениях, возникающих в процессе определения момента силы относительно осей, следует заменить отдельные силы эквивалентными совокупностями двух сил, для которых вычисления упрощаются. В ряде случаев полезно отображать проекции рассматриваемой системы на координатные плоскости.
Заметим, опуская доказательства, что подобно тому, как это было в плоской системе сил, составляя уравнения равновесия для пространственной системы сил, можно увеличивать число уравнений моментов относительно осей вплоть до шести, соблюдая некоторые ограничения, накладываемые на направление осей, такие, чтобы уравнения моментов были бы линейно независимы.
Задача 1.3. Прямоугольная плита, опертая в точке В на сферический
шарнир и закрепленная в точках А и С с помощью стержней, поддер-
живается в равновесии нитью, как показано на рис. 1.71. Определить реакции связей плиты ЛВС.

Рис. 1.71. Равновесие тела под действием пространственной системы сил
Д а н о: G, т, Za, Z(3 = л/4.
Выбирая начало координат в точке В, выразим составляющие пространственно ориентированной реактивной силы Т по оси z и плоскости Вху:
Т7 =Т cosa; TXY = Т sin a.
Условия равновесия для данной системы будут представлять систему последовательно решаемых уравнений, которые запишем, опуская пределы суммирования, в виде:
X mz = 0- -ХАа = 0;
=°’ Tza + Gm = 0;
X mxi = 0.
Х^ = о, X Fn = 0;
Tza + Zca = 0;
= 0;
cosP
YB - Txy sin (3 = 0;
Проект подготовил студент группы 22-с
Рыбаков Илья Семёнович
|
|
|
|
 Скачать 236.86 Kb.
Скачать 236.86 Kb.