Основы теории цифровых устройств. Проверил Борщинский М. Ю

• Название: Проверил Борщинский М. Ю
• Анкор: Основы теории цифровых устройств
• Дата: 06.01.2023
• Размер: 267 Kb.
• Имя файла: 7_mikroprots_pravilny.doc
• Тип: Документы; #874148

Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное

учреждение высшего профессионального образования
«Сибирский государственный индустриальный университет»

Институт информационных технологий и автоматизированных систем
Кафедра автоматизированного электропривода

и промышленной электроники

МИНИМИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
Вариант 7
Выполнил: Сердов В.А

Группа ЗЭТП-21

Проверил: Борщинский М.Ю.

г. Новокузнецк 2022

Разработать схемы на логических и релейно-контакторных элементах для реализации логических функций четырех аргументов

x	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
y	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
z	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
v	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
	1	0	1	1	1	0	0	0	1	1	0	0	1	0	1	0

Логическую функцию представить в виде ДНФ и в виде КНФ. Минимизацию логической функции проводить с помощью карт Карно и при помощи логических преобразований. Разработку провести на базе следующих типов элементов:

1) 2И, 2ИЛИ, НЕ.

2) 2И-НЕ.

3) 2ИЛИ-НЕ.
Таблица 1 – Таблица истинности логической функции

0	0	0	0	0	1		-
1	0	0	0	1	0	-
2	0	0	1	0	1		-
3	0	0	1	1	1		-
4	0	1	0	0	1		-
5	0	1	0	1	0	-
6	0	1	1	0	0	-
7	0	1	1	1	0	-
8	1	0	0	0	1		-
9	1	0	0	1	1		-
10	1	0	1	0	0	-
11	1	0	1	1	0	-
12	1	1	0	0	1		-
13	1	1	0	1	0	-
14	1	1	1	0	1		-
15	1	1	1	1	0	-

Логическое выражение заданной логической функции можно представить в виде ДНФ как логической суммы минтермов mi или в виде КНФ как логического произведения макстермов Mi:

ДНФ:



КНФ:



Логическая функция в ДНФ преимущественно реализуется на логических элементах И, И-НЕ. Логическая функция в КНФ преимущественно реализуется на элементах ИЛИ, ИЛИ-НЕ.

Карта Карно представляет собой таблицу, в которой представлены все минтермы. Каждый минтерм изображается на карте в виде клетки. Минтермы соседних клеток отличаются только значением одной переменной. Соседними также считаются крайние клетки каждого столбца или строки. Символ «1» обозначает прямое значение переменной, а «0» – инверсное значение переменной. Минтермы, входящие в функцию, отмечают единицами в соответствующих клетках карты. Для минтерма, не входящего в функцию, в клетках проставляется нуль или клетка остаётся пустой. Карта Карно логической функции приведена на рисунке 1.

На карте Карно отмечаются группы, состоящие из 2n ячеек, кратных 2 (2, 4, 8, …), и содержащие 1.

	00	01		11	10
00	1		1	1	1
01	0		0	0	1
11	1		0	0	0
10	1		0	1	0

Рисунок 1 – Карта Карно

Минимизированное выражение, описывающее логическую функцию, представляет собой дизъюнкцию полученных при помощи карт Карно логических выражений. В результате получаем выражение в дизъюнктивной нормальной форме (ДНФ):





Для реализации логической функции на элементах И-НЕ преобразуем полученное выражение в базис элементов И-НЕ:





Рисунок 2 – Принципиальная схема на элементах 2И-НЕ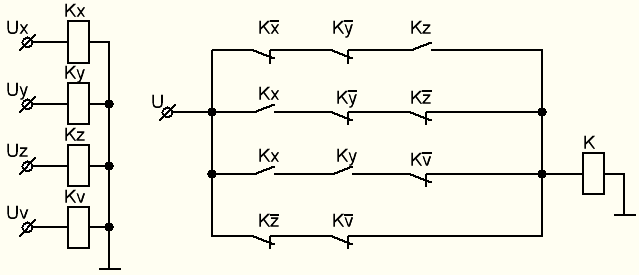



Рисунок 3 – Релейно-контактная схема устройства

	00	01		11	10
00	1		1	1	1
01	0		0	0	1
11	1		0	0	0
10	1		0	1	0

Рисунок 4 – Карта Карно





Для реализации логической функции на элементах ИЛИ-НЕ преобразуем полученное выражение в базис элементов ИЛИ-НЕ:





Рисунок 5 – Принципиальная схема на элементах 2ИЛИ-НЕ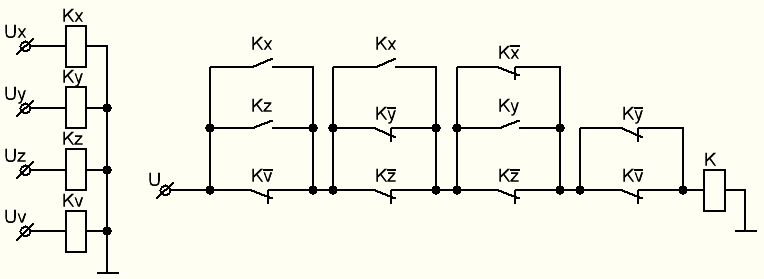



Рисунок 6 – Релейно-контактная схема устройства