Обработка результатов измерений. Прямыми называются измерения, сделанные при помощи приборов. Например, при помощи часов измеряется время, при помощи линейки измеряется расстояние, при помощи весов измеряется масса и так далее. Косвенные измерения
 Скачать 105.78 Kb. Скачать 105.78 Kb.
|
|
Для начала необходимо выучить несколько определений. Прямыми называются измерения, сделанные при помощи приборов. Например, при помощи часов измеряется время, при помощи линейки измеряется расстояние, при помощи весов измеряется масса и так далее. Косвенные измерения – это измерения, при которых значение измеряемой величины вычисляется при помощи значений, полученных посредством прямых измерений. Вот пример. Вы вольтметром измерили напряжение, амперметром измерили ток. Это прямые измерения. А сопротивление вы будете рассчитывать по закону Ома (R=U/I, если кто забыл). Результаты расчета сопротивления и будут косвенными измерениями. Выборка. Важно понимать, что в процессе эксперимента величина измеряется много раз. На самом деле, чем больше измерений, тем лучше (будет точнее результат), но в целях экономии времени ограничимся пятью измерениями. Здесь и далее в качестве примера я буду приводить лабораторную работу №1, в которой нужно взвешивать свинцовые шарики, бросать их в глицерин и засекать время, за которое они достигнут дна. Вы взяли весы и измерили массу шарика 5 раз. Полученный результат будет являться выборкой. То есть вы пять раз измерили одну и ту же величину. Если вы возьмете пять разных шариков и измерите их массы, то полученные результаты не будут выборкой, так как это разные шарики, у них разная масса. Запись результатов измерений выглядит обычно так:
Можно заметить, что значения очень близки. Это позволяет понять, выборка перед вами или нет. Все расчеты погрешностей можно проводить только с выборками. Переходим к обработке результатов прямых измерений 1. Устранить из выборки очевидные промахи (описки). Это делается просто исходя из логики и здравого смысла. Например, все тот же свинцовый шарик. Его масса 120 мг, все результаты измерений практически одинаковые и находятся в районе 120 мг. Но если вдруг в выборку попало какое-то резко выбивающееся значение (например, 130 мг), то его можно смело выкинуть. 2. Из результатов измерений исключить известные систематические погрешности. Систематические погрешности могут быть связаны с неисправностью или несовершенством приборов (неправильная шкала, калибровка и т. п.), неучтёнными экспериментатором. Например, если измерения проводятся аналоговым прибором и стрелка находится не напротив нуля, то это и есть систематическая погрешность. 3. Упорядочить выборку в порядке возрастания ее элементов. Без комментариев. 4. Провести проверку выборки на наличие грубых погрешностей. Достаточно проверить только первый и последний элементы упорядоченной выборки, ведь если они не являются грубыми погрешностями, то и остальные значения в порядке. Сначала рассчитаем размах выборки по формуле:  , где xmax – это максимальное значение элемента в выборке, а xmin – минимальное. Необходимо отметить, что с буквами x, y, z в формулах вы будете встречаться очень часто. Они просто обозначают какие-то абстрактные величины или переменные. У вас в заданиях и лабораторных будут даны конкретные величины. В случае со шариком нам дана конкретная величина m – масса шарика, поэтому вместо x подставляем m и формула приобретает вид: , где xmax – это максимальное значение элемента в выборке, а xmin – минимальное. Необходимо отметить, что с буквами x, y, z в формулах вы будете встречаться очень часто. Они просто обозначают какие-то абстрактные величины или переменные. У вас в заданиях и лабораторных будут даны конкретные величины. В случае со шариком нам дана конкретная величина m – масса шарика, поэтому вместо x подставляем m и формула приобретает вид: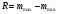 (1) (1)Дальше нужно рассчитать параметр u по формуле:  (2) (2)и сравнить его с коэффициентом uP, N. Так как вы проверяете крайние элементы выборки, то берем всего два значения: i = 1 и i = N-1 (N – число элементов в выборке, в нашем случае N = 5) Коэффициент uP, N зависит от размеров выборки и таблицу с его значениями можно найти в конце методички. Для удобства приведу эту таблицу и здесь.
В нашем случае размер выборки равен 5, а коэффициент uP,N= 0.64. Если ui > uP, Nпри i = 1, то xmin представляет собой элемент выборки, содержащий грубую погрешность. Аналогично, если ui > uP, N при i = N-1, то xmax представляет собой элемент выборки, содержащий грубую погрешность. Подставляем в формулу (2) значение i = 1 и получаем: 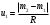 (3) (3)Сравниваем значение u1, полученное по формуле (3) с uP,N= 0.64. Если u1 > 0.64, то mmin является промахом, если u1 ≤ 0.64, то mmin промахом не является. Также поступаем в случае i = N-1. Получаем: 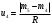 (4) (4)Сравниваем значение u4, полученное по формуле (3) с uP, N= 0.64. Если u4 > 0.64, то mmax является промахом, если u4 ≤ 0.64, то mmax промахом не является. В случае, если какое-либо значение оказалось грубой погрешностью, оно удаляется из выборки и размер выборки уменьшается. Соответственно меняется размах и коэффициент uP,N. После этого проверка на грубые промахи продолжается. 5. Вычислить выборочное среднее. После того, как из выборки исключены промахи и грубые погрешности вычисляется среднее арифметическое 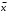 (в нашем случае (в нашем случае 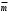 ). ).6. Вычислить среднеквадратическое отклонение (СКО). Нужно просто воспользоваться формулой: 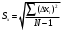 (5) (5)N – это размер выборки. Вот эта формула с раскрытой суммой в числителе:  (6) (6)Вместо x подставляем m. 7. Вычислить СКО среднего: 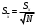 (7) (7)Подставляем, считаем. 8. Определить случайную погрешность: 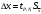 (8) (8)где 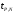 – это коэффициент Стьюдента. Как и uP, N, его тоже нужно брать из таблицы в конце методички. Приведу эту таблицу здесь: – это коэффициент Стьюдента. Как и uP, N, его тоже нужно брать из таблицы в конце методички. Приведу эту таблицу здесь:
9. Определить верхнюю границу погрешности прибора θx.Погрешность измерительного прибора со шкалой – половина цены деления. Погрешность цифрового измерительного прибора – последний разряд. 10. Рассчитать полную погрешность результата измерения: 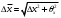 (9) (9)Тут тоже все просто, не забываем вместо x писать m. 11. Округлить числовые значения полной погрешности и результата измерения. Результат нужно записывать в виде  , в нашем случае , в нашем случае 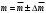 . Ничего не надо складывать и вычитать, так и пишите ±. Среднее было рассчитано в пункте 5, полная погрешность в пункте 10. . Ничего не надо складывать и вычитать, так и пишите ±. Среднее было рассчитано в пункте 5, полная погрешность в пункте 10.Предварительно результат и погрешность записывают в нормализованном экспоненциальном виде: общий показатель степени выносят за скобку или заменяют соответствующей приставкой: микро, мили, кило, мега и др. Небольшая справочка. Любое число может быть записано в виде M·10p многими путями; например, 350 может быть записано как 3.5·102 или 35·101. Это экспоненциальная запись числа. В нормализованной записи порядок p выбирается такой, чтобы абсолютная величина M оставалась не меньше единицы, но строго меньше десяти (1 ≤ M <10). Например, 350 записывается как 3.5·102. Вот пример записи результата измерения с погрешностью: x = 0.022 ± 0.003 м = (2.2 ± 0.3)·10–3 м = 2.2 ± 0.3 см. Запрещены записи вида x = 22·10–3± 30·10–4 м или x = 0.022 ± 3·10–3 м. Показатель 101 не выносится. После этого можно переходить к округлению. СНАЧАЛА ОКРУГЛЯЕТСЯ ПОГРЕШНОСТЬ! Первый пример: 7.854 ± 0.0476 Работаем с погрешностью, ищем первую значащую цифру. Значащая цифра – это любая цифра, кроме нуля. Просто слева направо начинаете перебирать все цифры. Смотрим на погрешность. Первая цифра 0, не подходит. Вторая 0, не подходит. Третья цифра 4, отлично, это первая значащая цифра. Если она больше 2, то до нее и округляем погрешность. В нашем случае получается 0.05. Если первая значащая цифра 2 и меньше, то округляем до соседней цифры, то есть до двух значащих цифр. Второй пример: 83.2637 ± 0.0126. Первая значащая цифра 1, поэтому округляем до соседней и получаем 0.013. Если погрешность округляется до двух значащих цифр, но вторая из них равна нулю, то этот нуль сохраняется, а в соответствующем ему разряде результата записывается получающаяся там значащая цифра: x = 3.48 ± 0.10. После того, как вы округлили погрешность, можно работать со средним. Тут все просто, среднее значение округляют до того разряда, которым оканчивается округленная погрешность. В первом примере правильно записанный ответ выглядит как 7.85 ± 0.05, а во втором 83.264 ± 0.013 12. Записать окончательный результат в виде  Записываем то, что получилось после округления и на этом обработка результатов прямых измерений окончена. Переходим к обработке косвенных измерений. Первый способ – это метод переноса погрешности или метод полного дифференциала. Его можно использовать только в том случае, если измеренные величины не зависят друг от друга. Если вы несколько раз взвесили шарик, а потом несколько раз засекли время, за которое он достигает дна, то вы получите две выборки (масса и время), так как были проведены независимые серии опытов. Количество элементов в выборках не обязательно может быть одинаковым, мы может 100 раз взвесить шарик и 50 раз засечь время, на конечный результат это никак не повлияет. Переходим к алгоритму обработки. Формула для расчета вязкости выглядит следующим образом: 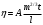 (10) (10)где A – это константа, зависящая от свойств исследуемой жидкости, l – расстояние, которое проходит шарик в жидкости, m – масса шарика, t – время, за которое он проходит расстояние l. Видно, что искомая величина вязкости зависит от двух переменных: m и t. Это записывается следующим образом:  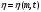 . В общем виде это выглядит так: . В общем виде это выглядит так: 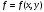 . Функция не обязательно зависит от двух переменных, их может любое количество. . Функция не обязательно зависит от двух переменных, их может любое количество.1. По формулам прямых измерений определить величины 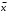 , , 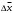 , , 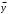 , , 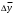 . .При помощи алгоритма обработки прямых измерений необходимо рассчитать средние значения и полные погрешности данных величин, в нашем случае массы и времени ( 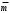 , , 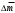 , , 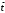 , , 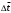 ) )2. Рассчитать среднее значение функции 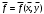 Чтобы это сделать, вам просто нужно подставить средние значения, рассчитанные в пункте 1, в формулу 10 и получить 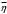 3. Вычислить в точке 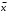 , , 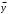 частные производные от функции. частные производные от функции. , , 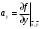 Главный вопрос здесь – это что такое частные производные и как их вычислять. На самом деле все очень просто. Так как функция зависит сразу от нескольких переменных, то и производные надо брать по каждой переменной в отдельности. Немного преобразуем формулу: 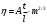 (11) (11)Я просто переставил местами буквы для наглядности. Рассчитаем производную по m. В этом случае всё, кроме m, будем считать константами. То есть 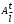 – это просто некая константа. Получаем: – это просто некая константа. Получаем:  (12) (12)Аналогично поступим с другой переменной. Преобразуем формулу: 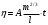 (13) (13)Рассчитаем производную по t: 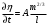 (14) (14)Теперь подставляем значения 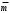 и и 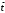 в формулы (12) и (14) и рассчитываем am и at. в формулы (12) и (14) и рассчитываем am и at. 4. Вычислить полную погрешность по формуле 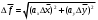 В нашем случае формула записывается как  . Подставляем, считаем. . Подставляем, считаем.5. Записать окончательный результат в виде 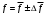 В нашем случае 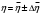 . Правила округления те же самые. . Правила округления те же самые.Второй способ обработки результатов косвенных измерений – это выборочный метод. Он применяется в том случае, если значения каждой из совместно измеренных величин не образуют выборок. Например, вы берете 5 разных шариков, взвешиваете их, бросаете в жидкость и засекаете время, за которое они достигнут дна. Каждому шарику с определенной массой будет соответствовать свое определённое время. Это совместное измерение величин. Выборок такие измерения не образуют, поэтому для дальнейшей обработки выборку нужно создать. 1. По каждому набору совместно измеренных значений аргументов рассчитать значения функции 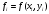 . .Берем первую пару значений m1 и t1, поставляем их в формулу (10), получаем η1. Потом пару m2 и t2, получаем η2 и так далее. В результате получается выборка значений {ηi}. 2. Обработать полученную выборку {fi} согласно алгоритму обработки данных прямых измерений, находя среднее значение 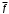 и случайную погрешность и случайную погрешность 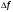 функции. функции.Обратите внимание, что в отличие от метода переноса погрешности, нужно найти только случайную погрешность, так как для искомой функции нет приборной погрешности. 3. Вывести выражения для частных производных функции ax и ay. Вывод формул ничем не отличается от описанного в пункте 3 для метода переноса погрешности. В результате получаем формулы (12) и (14). 4. Рассчитать средние значения 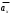 и и 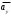 по формулам: по формулам: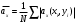 , , 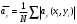 В формулы (12) и (14) нужно подставить пары измеренных значений (xi, yi), по аналогии с первым пунктом. В результате получается набор значений axiиayi, а потом просто вычисляется среднее. 5. Вычислить приборную погрешность функции 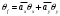 Берем данные из пункта 4, приборную погрешность и считаем. 6. Вычислить полную погрешность функции 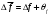 Случайную погрешность берем из пункта 2, приборную из пункта 5. 7. Записать окончательный результат в виде 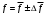 В нашем случае 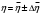 . Правила округления те же самые. . Правила округления те же самые. |
