Рабочая тетрадь № 4
Высказывание – это утверждение, которое может принимать два значения: истина, либо ложь.
Если высказывание A ложно, то будем записывать A = 0, иначе A = 1.
Математическая логика не касается вопросов ложности или истинности конкретных высказываний [1]. Здесь высказывания X, Y, Z –переменные, которые могут быть ложными или истинными.
Операции с переменными, принимающими такие значения, называются булевой алгеброй (алгеброй логики).
|
1. Теоретический материал
|
Пусть A и B – высказывания. С этими высказываниями можно выполнять следующие основные логические операции:
отрицание «НЕ»: ¬A
конъюнкция «И»: A&B
дизъюнкция «ИЛИ»: A˅B
импликация «следует»: A → B
эквивалентность: A B.
Элементарные логические операции
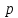
|
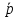
|
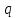
|
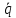
|
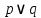
|
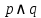
|
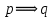
|
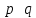
|
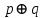
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
Приоритет выполнения операций:
Сначала выполняются действия в скобках. Затем выполняется операция отрицания (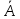 ), далее – конъюнкция ( ), далее – конъюнкция (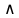 ), дизъюнкция ( ), дизъюнкция (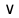 ), импликация ( ), импликация (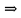 ) и в последнюю очередь – эквивалентность ( ) и в последнюю очередь – эквивалентность ( ). Однотипные операции выполняются в порядке следования. ). Однотипные операции выполняются в порядке следования.
Таблица истинности – это набор всевозможных комбинаций переменных с указанием значения логической формулы. Такая таблица, описывает логическую функцию.
|
2. Пример
|
Задача:
|
|
Приведите таблицу истинности для следующего выражения
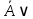 B B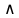 A A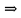 B B
|
Решение:
|
|
A
|
B
|
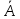
|
B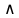 A A
|
(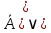 B B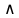 A) A)
|
(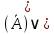 B B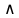 A A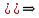 B B
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
|
|
0
|
1
|
1
|
1
|
|
Задача:
|
|
Для какого из представленных вариантов символьных строк следующее высказывание является ложным:
(Первая буква гласная) → ¬(Третья буква согласная) ?
1) abedc; 2) babas; 3) becde; 4) abcab.
|
Решение:
|
|
Логическое выражение является импликацией. Данная логическая функция ложна только в том случае, когда из истинной левой части высказывания следует ложная правая часть. Левая часть будет истинной для вариантов один и четыре. Правая часть является отрицанием высказывания «третья буква согласная» (что эквивалентно высказыванию«третья буква гласная»). При этом правая часть ложна для вариантов два, три и четыре. Следовательно, правильный вариант расположен под номером 4.
|
Ответ:
|
|
4
|
Задача:
|
|
Какое из представленных выражений равносильно следующему:
A ∨ ¬(¬B ∧ ¬C) ?
1) ¬A∨¬B∨¬C; 2) A ∧ ¬(B ∧ C);
3) A∨¬B∨¬C; 4) A ∨ B ∨ C.
|
Решение:
|
|
Задействуем законы де Моргана. Раскрыв скобки запишем:
A ∨ ¬(¬B ∧ ¬C) = A ∨ (¬¬B ∨ ¬¬C).
Теперь применим закон двойного отрицания:
A ∨ (¬¬B ∨ ¬¬C) = A ∨ B ∨ C.
Следовательно, правильный вариант четвертый.
|
Ответ:
|
|
4
|
Задача:
|
|
По заданному фрагменту таблицы истинности для выражения F определить, какое из перечисленных ниже логических выражений ему соответствует [5].
X
|
Y
|
Z
|
F
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
1) ¬X ∧ ¬Y ∧ Z; 2) X ∨ ¬Y ∨ ¬Z;
3) ¬X ∧ ¬Y ∧ Z; 4) ¬X ∨ ¬Y ∨ Z.
|
Решение:
|
|
Подставим представленные значения X, Y и Z из таблицы во все варианты логических функций.
Для первого выражения получим:
¬1 ∧ ¬0 ∧ 0 = 0 ∧ 1 ∧ 0 = 0;
¬0 ∧ ¬0 ∧ 1 = 1 ∧ 1 ∧ 1 = 1;
¬0 ∧ ¬1 ∧ 0 = 1 ∧ 0 ∧ 0 = 0.
Для второго выражения получим:
1 ∧ 0 ∧ ¬0 = 1 ∧ 0 ∧ 1 = 0;
0 ∧ 0 ∧ ¬1 = 0 ∧ 0 ∧ 0 = 0;
0 ∧ 1 ∧ ¬0 = 0 ∧ 1 ∧ 0 = 0.
Для третьего выражения получим:
1 ∨ ¬0 ∨ ¬0 = 1 ∨ 1 ∨ 1 = 1;
0 ∨ ¬0 ∨ ¬1 = 0 ∨ 1 ∨ 0 = 1;
0 ∨ ¬1 ∨ ¬0 = 0 ∨ 0 ∨ 1 = 1.
Для четвертого выражения получим:
¬1 ∨ ¬0 ∨ 0 = 0 ∨ 1 ∨ 0 = 1;
¬0 ∨ ¬0 ∨ 1 = 1 ∨ 1 ∨ 1 = 1;
¬0 ∨ ¬1 ∨ 0 = 1 ∨ 0 ∨ 0 = 0.
Таким образом, сопоставив приходим к выводу, что правильный вариант под номером один.
|
Ответ:
|
|
1
|
Задача:
|
|
Найдите наименьшее целое число x> 0, при котором логическое выражение (4 > –(4 + x) x) → (30 > x ⋅ x) является ложным?
|
Решение:
|
|
Импликация ложна только в случае, если левая часть выражения истинна, а правая ложна.
Рассмотрим левую часть. После преобразований можно записать квадратное неравенство x2 + 4x + 4 > 0 или (x + 2)2> 0. Поскольку x> 0, левая часть импликации истинна всегда. Выражение (30 > x⋅x) будет ложным для x > 5. ( 30 > 52, но 30 < 62). Следовательно наименьшее целое число x большее нуля, для которого высказывание ложно равно 6.
|
Ответ:
|
|
6
|
Задача:
|
|
Перед началом соревнований три зрителя высказали предположения по поводу победителей:
Коля победит, Петя будет вторым;
Петя– третий, Ваня– первый;
Коля будет последним, а первым будет Женя.
Когда турнир окончился, оказалось, что каждый из зрителей был прав только в одном прогнозе из двух. Какое место на соревнованиях заняли Женя, Ваня, Петя и Коля? В ответе перечислите места участников в указанном порядке имен.
|
Решение:
|
|
Обозначим буквами предсказания каждого зрителя [5].
Первый: A — Коля победит; B — Петя второй.
Второй: C — Петя третий; D — Ваня первый.
Третий: E — Коля последний; F — Женя первый.
Нетрудно заметить, что истинными одновременно не могут быть выражения B и C; A и E; A и D; A и F; D и F.
Поскольку из условия известно, что в каждом из прогнозов одно высказывание ложно, а другое истинно, то получаем следующее:
A¬B ∨ ¬AB = 1;
C¬D ∨ ¬CD = 1;
E¬F ∨ ¬EF = 1.
Так как все условия должны быть истинными одновременно справедливо следующее выражение:
(A¬B ∨ ¬AB)(C¬D ∨ ¬CD)(E¬F ∨ ¬EF) = 1.
Раскроем скобки. Используя логические законы, рассмотренные ранее, получим:
A¬BC¬DE¬F ∨ ¬ABC¬DE¬F ∨ A¬B¬CDE¬F ∨
∨ ¬AB¬CDE¬F ∨ A¬BC¬D¬EF ∨ ¬ABC¬D¬EF ∨
∨ A¬B¬CD¬EF ∨ ¬AB¬CD¬EF = 1.
Учитывая, что BC = 0, AE = 0, AD = 0, AF = 0, DF = 0, получаем следующее:
¬AB¬CDE¬F = 1.
Представленная конъюнкция равна единице, если все сомножители равны единице, следовательно:
A = 0; B = 1; C = 0; D = 1; E = 1; F = 0.
Вспоминая высказывания каждого из зрителей, получаем, что Петя — второй, Ваня — первый, Коля — последний, т. е. четвертый. Таким образом, Женя на третьем месте. Следовательно, правильный ответ — 3124.
|
3. Задания
|
1.
|
Задача:
|
|
Составить таблицу истинности для выражений
1) AvB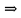 AB AB
2) 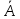 v( v(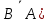 ⊕B (⊕ – исключающее ИЛИ, сумма по модулю 2) ⊕B (⊕ – исключающее ИЛИ, сумма по модулю 2)
3) AvB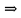 C C
|
Решение:
|
|
A-0011, B-0101, AvB-0111, AvB->A-1011, AvB->AB-0001
A-0011, B-0101, -A-1100, -(BA)-0111, -Av-(BA)-1111,
-Av-(BA) ⊕B-1010
A-00001111, B-00110011, C-01010101, AvB-00111111,
AvB->C-11010101
|
2.
|
Задача:
|
|
Для какого слова истинно высказывание:
(Первая буква гласная ∨ Пятая буква согласная) → Вторая буква гласная?
1) арбуз; 3) кресло; 2) ответ; 4) привет.
|
Решение:
|
|
0 или 0 -> 0 = 1
|
Ответ:
|
|
4
|
3.
|
Задача:
|
|
Выберете логическое выражение эквивалентное следующему:
¬(¬A ∧ B) ∨ ¬C?
1) ¬A ∨ B ∨ ¬C; 2) A ∨ ¬B ∨ ¬C;
3) ¬A ∨ ¬B ∨ ¬C; 4) A ∨ B ∨ ¬C.
|
Решение:
|
|
A ∨ ¬B ∨ ¬C
|
Ответ:
|
|
2
|
4.
|
Задача:
|
|
По заданному фрагменту таблицы истинности для выражения F определить какое из перечисленных ниже логических выражений ему соответствует.
X
|
Y
|
Z
|
F
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
1) X ∧ Y ∧ Z; 2) X ∧ Y ∨ Z;
3) ¬X ∨ Y ∨ ¬Z; 4) X ∨ Y ∧ ¬Z.
|
Решение:
|
|
X ∨ Y ∧ ¬Z.
|
Ответ:
|
|
4
|
5.
|
Задача:
|
|
Найдите наибольшее целое число x> 0, для которого ложно выражение:
((x + 6) ⋅ x + 9 > 0) → (x ⋅ x > 20) .
|
Решение:
|
|
((x2+6x+9>0)->(x2>20)
((x+3)2>0)->(x2>20)
Импликация ложна только в случае, если левая часть выражения истинна, а правая ложна
Поскольку x> 0, левая часть импликации истинна всегда. Выражение (x2>20) будет ложным для x > 5. ( 42 >20 , но 20 < 52).
x=4
|
Ответ:
|
|
4
|
6.
|
Задача:
|
|
Найдите значения логических переменных A, B, C, D, при которых логическое выражение (¬(C∨B) ∧A) → ((¬A∧ ¬C) ∨D) = 0.
|
Решение:
|
|
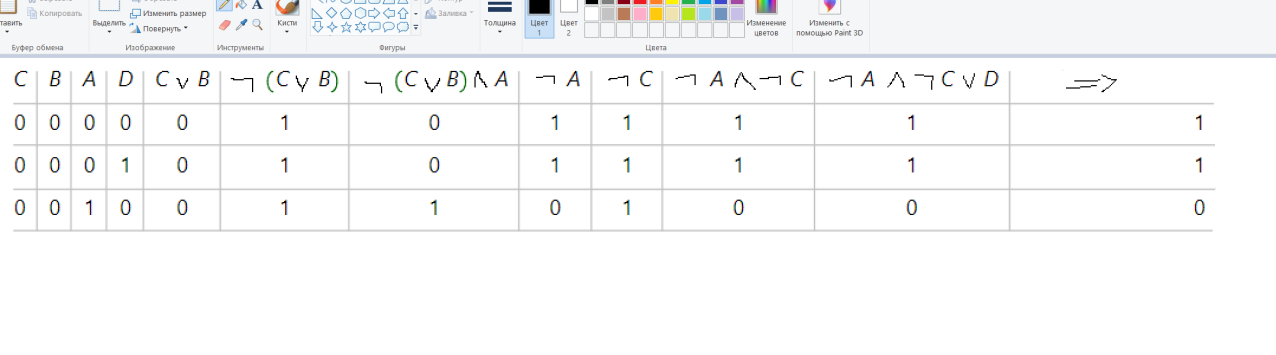
|
Ответ:
|
|
A=1, B=0, C=0, D=0
|
7.
|
Задача:
|
|
В соревновании участвовало пять человек: Аня, Надя, Вера, Рита, Саша. Об итогах турнира есть пять высказываний:
1. Первое место заняла Аня, а Рита – третья.
2. Пятая Вера, а вот Надя первая.
3. Первая Саша, а Вера– вторая.
4. Рита пятая, а Надя была четвертой.
5. Надя была четвертой, а первой — Аня.
Известно, что в каждом утверждении только одно утверждение из двух истинно. Требуется найти, кто занял первое место, и на каком месте была Аня? Ответ следует записать в виде первой буквы имени победительницы, и, через запятую, места, занятого Анной.
|
Решение:
|
|
P-3,B-5,C-1,H-4, A-2
|
Ответ:
|
|
C, 2
|
Тест 4
|
1.
|
Задание:
|
|
Таблица, включающая всевозможные значения логической функции, называется:
|
Ответ:2
|
|
1) таблица ложности; 2) таблица истинности;
3) таблица значений; 4) таблица ответов.
|
2.
|
Задание:
|
|
Значение логического выражения ¬(А٧В) по закону Моргана равно:
|
Ответ:1
|
|
1) ¬А&¬В; 2) ¬А&В; 3) А&¬В; 4) ¬А٧¬В.
|
3.
|
Задание:
|
|
Какое из перечисленных имен удовлетворяет истинности высказывания:
¬ (Первая буква согласная → Третья буква гласная) ?
|
Ответ:2
|
|
1) Ирина; 2) Сергей; 3) Григорий; 4) Ольга.
|
4.
|
Задание:
|
|
Выберете выражение эквивалентное следующему:
¬A ∨ ¬(B ∧ C)?
|
Ответ:1
|
|
1) ¬A ∨ ¬B ∨ ¬C; 2) ¬A ∧ B ∧ C;
3) A ∧ ¬B ∧ C; 4) (¬A ∨ B) ∧ C.
|
5.
|
Задание:
|
|
По заданному фрагменту таблицы истинности для выражения F определить какое из перечисленных ниже логических выражений ему соответствует.
X
|
Y
|
Z
|
F
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
1
|
|
Ответ:4
|
|
1) ¬X ∨ ¬Y ∨ ¬Z; 2) X ∧ Y ∧ Z;
3) X ∧ ¬Y ∧ ¬Z; 4) X ∨ Y ∨ Z.
|
6.
|
Задание:
|
|
Для какого из приведенных значений x выражение (x > 2)∨(x > 5)→(x < 3) истинно.
|
Ответ:3
|
|
1) 5; 2) 3; 3) 4; 4) 2.
|
7.
|
Задание:
|
|
Для какого из приведенных значений x выражение
¬((x > 2) → (x > 3)) = 1 .
|
Ответ:3
|
|
1) 1; 2) 2; 3) 3; 4) 4.
|
8.
|
Задание:
|
|
Сколько разнообразных решений имеет выражение
A∧ ¬B∧C∧ ¬D∧ (E∨ ¬E) = 0 ,
A, B, C, D, T — логические переменные?
В качестве ответа требуется написать количество таких наборов.
|
Ответ:
|
|
30
|
9.
|
Задание:
|
|
Каково наибольшее целое число X, при котором истинно высказывание
(100 < X ⋅ X) → (100 > (X + 1)(X + 1)) ?
|
Ответ:
|
|
10
|
10.
|
Задание:
|
|
Четыре друга — Антон, Михаил, Николай и Виктор пришли в автосалон. Продавец сказал, что осталось только четыре машины: красная, черная, белая и синяя. Каждый из друзей купил по машине. Имеется три утверждения:
Красную машину купил Антон, а черную– Михаил;
Антон взял черный автомобиль, а Виктор – белый;
Николай забрал черное авто, а Виктор — синее.
Кто купил синюю машину, и какой автомобиль выбрал Виктор? Известно, что половина каждого утверждения ложна, а половина истинна.
Ответ требуется записать в виде первой буквы имени, взявшего синий автомобиль, и, через запятую, первую букву цвета машины Виктора.
|
Ответ:
|
|
М, Б
|
Реализация задач на языке программирования Python
1. Теоретический материал
|
В Python существует возможность работы с двоичными разрядами (битами) целых величин. При этом каждый бит числа рассматривается отдельно. Для этого в Python задействованы битовые (поразрядные) операторы, которые реализуют битовые операции.
В побитовых операторах (операциях) операнды рассматриваются как последовательность бит (нулей или единиц). Над разрядами существует возможность выполнять известные логические операции (логическое «ИЛИ», логическое «И», и т.д.).
Битовые операции в Python в порядке убывания приоритета представлены ниже:
Операции
|
Назначение
|
|
побитовое НЕ (инверсия);
|
<<,>>
|
битовые сдвиги влево и вправо;
|
&
|
побитовое И;
|
^
|
побитовое исключающее ИЛИ (XOR);
|
|
|
побитовое ИЛИ (OR).
|
В битовой инверсии значение любого бита числа меняется на противоположное. У числа при этом меняется знак со смещением на -1.
Операторы сдвига влево << и сдвига вправо >> сдвигают биты на одну или несколько позиций влево или вправо соответственно.
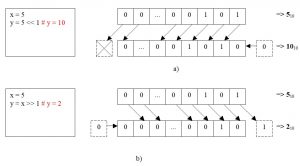
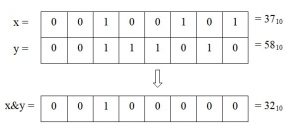
Битовый оператор И (AND) есть бинарным и выполняет побитовое «И» для каждой пары битов операндов, которые размещаются слева и справа от знака оператора &.
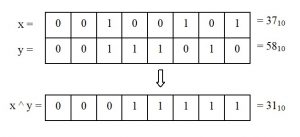
Битовый оператор «исключительное ИЛИ» обозначается ^ и выполняет операцию сложения по модулю 2 для любого бита операндов.
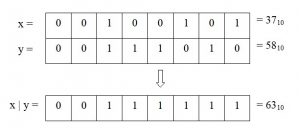
Битовый оператор ИЛИ (OR) символом |. Оператор реализует побитовое логическое сложение.
|
2. Пример
|
Задача:
|
|
Дано число x = 37, y = 58.
Найти x, x>>3, x<<2, x&y, x^y, x|y
|
Решение (код программы):
|
|
x, y = 37, 58
#x в десятичной и двоичной системе
print('x = ', x, ' x_bin = ', bin(x))
#y в десятичной и двоичной системе
print('y = ', y, ' y_bin = ', bin(y))
#x в десятичной и двоичной системе
a = x
print('x =', a, ' x_bin = ', bin(a))
#x>>3 в десятичной и двоичной системе
b = x >> 3
print('x>>3 =', b, ' (x>>3)_bin = ', bin(b))
#x<<2 в десятичной и двоичной системе
c = x << 2
print('x<<2 =', c, ' (x<<2)_bin = ', bin(c))
#x&y в десятичной и двоичной системе
d = x & y
print('x&y =', d, ' (x&y)_bin = ', bin(d))
#x^y в десятичной и двоичной системе
e = x ^ y
print('x^y =', e, ' (x^y)_bin = ', bin(e))
#x|y в десятичной и двоичной системе
f = x | y
print('x|y =', f, ' (x|y)_bin = ', bin(f))
|
Задача:
|
|
Вытянуть из числа 4,5,6 биты и определить их целочисленное значение.
|
Решение (код программы):
|
|
number = int(input('Input number: '))
# фильтр на 4,5,6 биты
number &= 0b1110000
# сдвинуть на 4 разряда вправо
number >>= 4
print('number = ', number)
|
Задача:
|
|
Умножить значения двух чисел. В первом числе взять биты, которые размещенные в позициях 0-5. Во втором числе взять биты, которые размещены в позициях 0-7.
|
Решение (код программы):
|
|
x = int(input('x = '))
y = int(input('y = '))
# фильтр на 0-5 биты
x &= 0b11111
# фильтр на 0-7 биты
y &= 0b1111111
# умножить
z = x*y
print('x = ', x)
print('y = ', y)
print('z = ', z)
|
3. Задания
|
Задача:
|
|
Даны два различных числа k и n. Выведите значение 2k+ 2n, используя только битовые операции.
|
Решение (код программы):
|
|
k=int(input())
n=int(input())
print(2**k+2**n)
|
Задача:
|
|
Ввести число n > 0 с клавиатуры. Если число n является точной степенью двойки, вывести “YES”, в противном случае “NO”.
|
Решение (код программы):
|
|
n = int(input())
i = 1
while i < n:
i = i * 2
if i == n:
print("YES")
else:
print("NO")
|
Задача:
|
|
Даны целые числа a и k. Выведите число, которое получается из а установкой значения k-го бита в 1.
|
Решение (код программы):
|
|
a=int(input())
k=int(input())
print(a|(1< |
Задача*:
|
|
Дано целые числа n и k. Обнулите в числе n его последние k бит и выведите результат. Рекомендуется сделать эту задачу без использования циклов.
|
Решение (код программы):
|
|
n=int(input())
k=int(input())
print((n>>k)< | |
 Скачать 157.81 Kb.
Скачать 157.81 Kb.