Лекция 4. Ранговая корреляция

• Название: Ранговая корреляция
• Дата: 15.03.2023
• Размер: 4.92 Mb.
• Имя файла: Лекция 4.docx
• Тип: Закон; #991482

Ранговая корреляция

До сих пор был анализ зависимости между количественными переменными с известным законом распределения, над которыми можно было совершать арифметические операции.

Рассмотрим корреляцию порядковых переменных.

Если по некоторой дисциплине два студента имеют оценки «отлично» и удовлетворительно, то можно лишь сказать, что уровень подготовки первого студента выше, чем второго. Но нельзя сказать во сколько раз. Объекты анализа упорядочиваем в порядке увеличения или порядке уменьшения степени выраженности исследуемого признака (ранжируем) и каждому объекту присваивается ранг.

Если объекты ранжированы по двум признакам, то имеется возможность оценить тесноту связи между признаками, основываясь на рангах, то есть тесноту ранговой корреляции.

Если будет высокая ранговая корреляция между признаками, то достаточно контролировать состояние объекта только по двум признакам.

Рассмотрим выборку объема n, объекты которого имеют два признака А и В.

В дальнейшем считаем, что n<=30

Критерий Спирмена

Случай 1. Все объекты имеют разное качество по каждому признаку (несвязанные ранги)

1. 
   Расположим объекты выборки в порядке улучшения качества по признаку А:
   

   А:	X1	X2	X3	…	Xn
   В:	Y1	Y2	Y3	…	Yn

2. 
   Присвоим объектам порядковые номера – ранги – по признаку А: a i i  .
   
3. 
   Ранжируем объекты по признаку В, присваивая порядковые номера – ранги i b , при этом индекс i равен рангу по признаку А.
   
4. 
   Составим две последовательности соответствующих друг другу рангов:
   

аi	1	2	3	…	n
А:	X1	X2	X3	…	Xn
В:	Y1	Y2	Y3	…	Yn
Bi	B1	B2	B3	…	Bn
Di	D1	D2	D3	….	Dn
Di^2

Коэффициентом ранговой корреляции Спирмана называется число: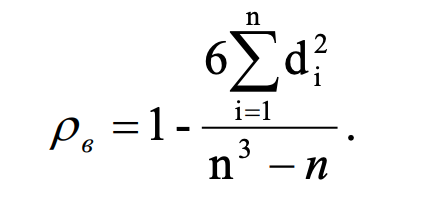



Значение rc является выборочной оценкой коэффициента ранговой корреляции генеральной совокупности.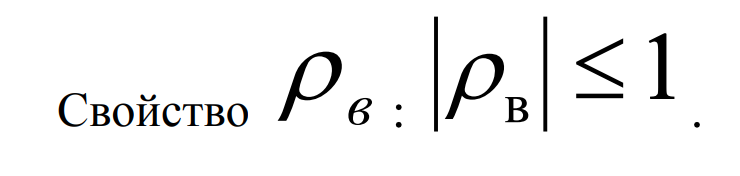



Рассматриваем при уровне значимости а проверку гипотезы:

H0 :  в  0 (связь между признаками нет)

H1 : в  0

Алгоритм проверки значимости коэффициента корреляции Спирмена

1. 
   Расчитать
   

2. 
   По таблице для распределения Стьюдента по уровню значимости а и числу степеней свободы k=n=2 найти tкритич
   
3. 
   Если |tв|  Tкрит , то принимаем гипотезу H0 и ранговая корреляция не значима;
   
4. 
   Если |в| = Tкрит , то принимаем гипотезу H1 и ранговая корреляция значима.
   

Зависимость tв объема выборки приводит к тому, что чем больше объем выборки, тем меньше величине коэффициента корреляции оказывается достаточно, чтобы корреляция была признана значимой. В результате при малом объеме выборки может оказаться так, что сильная корреляция окажется незначимой. В то же время при больших объемах выборки даже слабая корреляция может оказаться значимой.

Пример 1

Два эксперта на конкурсе красоты: мужчина и женщина оценивают моделей и для этого проставили места для каждой модели

Оценки эксперта-мужчины	4	2	5	1	3	6	7	8	9	10
Оценки эксперта-женщины	2	6	7	3	1	10	4	8	5	9

Расположим объекты выборки в порядке ухудшения качества по оценкам экспертов-мужчин и расставим ранги]6 которые равны самим экспертным оценкам:

аi	1	2	3	5	6	7	8	9	10	11
Оценки эксперта-мужчины	4	2	5	1	3	6	7	8	9	10
Оценки эксперта-женщины	3	6	1	2	7	10	4	8	5	9
bi	3	6	1	2	7	10	4	8	5	9
di	-2	-4	2	2	-2	-4	3	0	4	1
di^2	4	16	4	4	4	16	9	0	16	1

Сумма di^2= 74

Следовательно связь в выборке на среднем уровне, если она значима

Проверка значимости: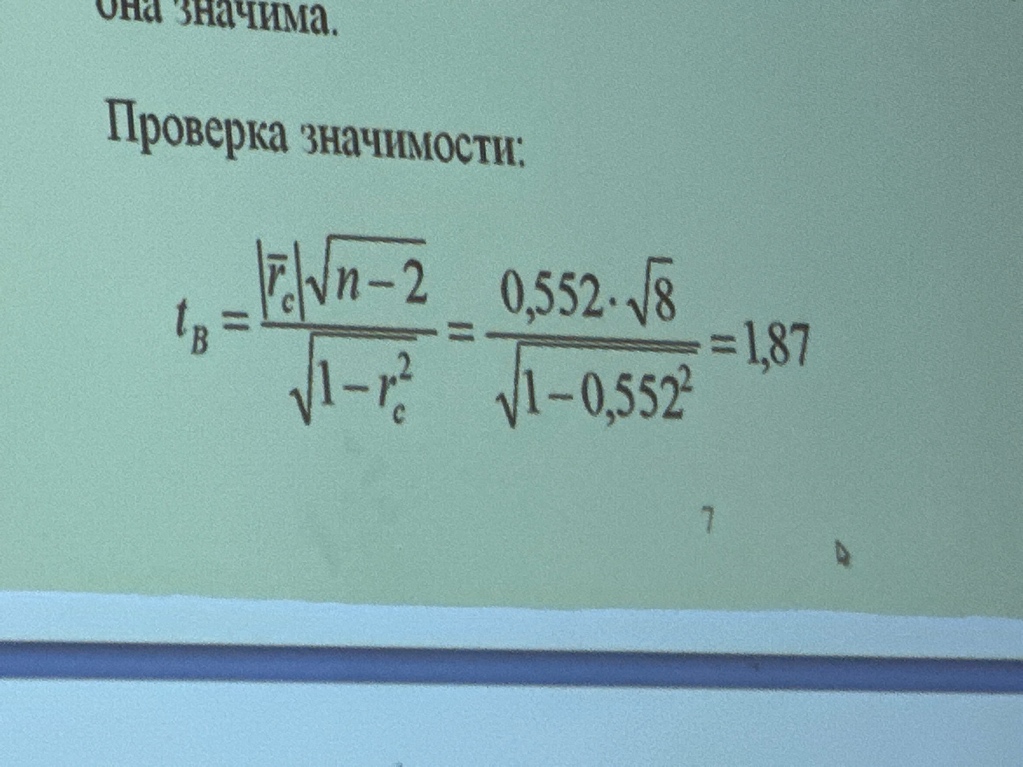

Открываем распределение Стьюдента

Пример 2
Анализирую связь между результатами экзаменов по статистике и по психологии (по 100 бальной системе). В выборке результаты экзаменов 8 студентов.

Оценки по психологии	22	49	44	50	57	10	25	17
Оценки по статистике	17	43	23	30	42	20	32	28

Расположим объекты выборки в порядке ухудшения качества оценки по психологии и расставим ранги.

аi	1	2	3	4	5	6	7	8
А	57	50	49	44	25	22	17	10
В	42	30	43	23	32	17	28	20
bi	2	4	1	6	3	8	5	7

Вычислим разность рангов

аi	1	2	3	4	5	6	7	8
А	57	50	49	44	25	22	17	10
В	42	30	43	23	32	17	28	20
bi	2	4	1	6	3	8	5	7
di	1	2	-2	2	-2	2	-2	-1
di2	1	4	4	4	4	4	4	1

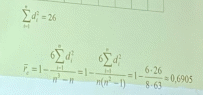Проверка значимости: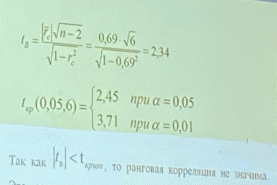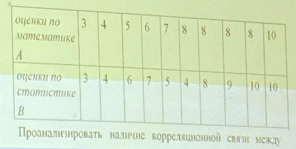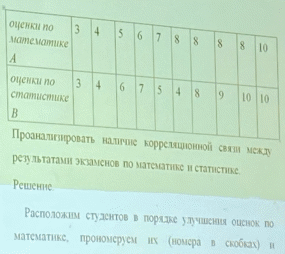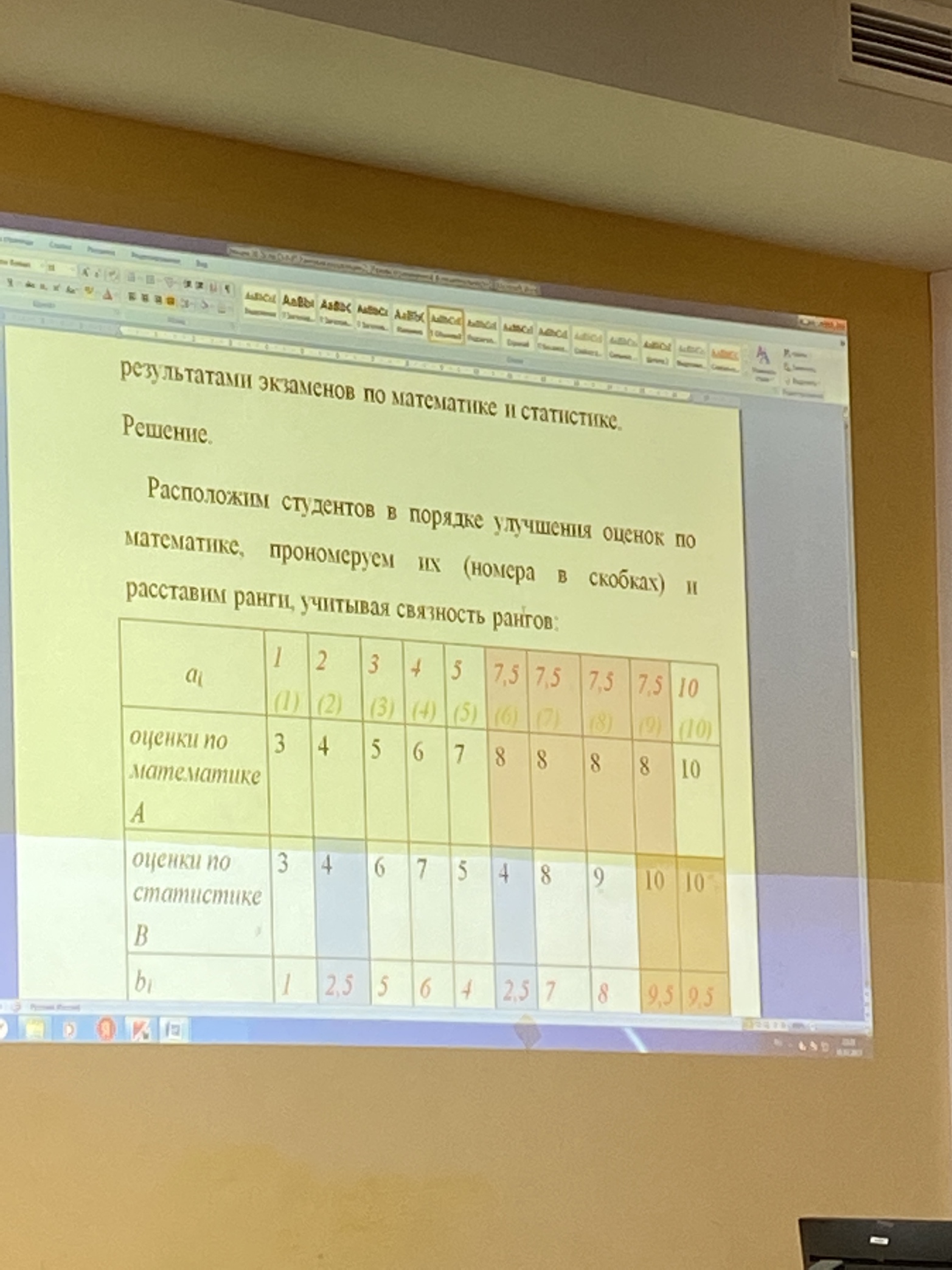






Если число встречается всего один раз, то ранг совпадает с числом, а если число встречается два раза, то мы должны сложить порядковые номера и поделить на 2