Расчет нестационарного температурного поля в двухслойной бесконечной пластине (изолированном стержне) с заданными начальными и граничными условиями
 Скачать 98.78 Kb. Скачать 98.78 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Волгоградский государственный технический университет Кафедра «Оборудование и технология сварочного производства» Семестровая работа по курсу: «Тепловые процессы в сварке» Расчет нестационарного температурного поля в двухслойной бесконечной пластине (изолированном стержне) с заданными начальными и граничными условиями Выполнил: Агеев Виктор Группа: МС-328 Проверил: Хаустов С. В. Волгоград 2022 ЗАДАНИЕ Вариант №1 Студент Агеев Виктор Группа МС-328 Тема: Расчет нестационарного температурного поля в двухслойной бесконечной пластине (изолированном стержне) с заданными начальными и граничными условиями Исходные данные для выполнения работы: Геометрия задачи, начальные и граничные условия:  Рассчитать: -температурное поле в двухслойной пластине через 1 сек. -термический цикл в сечении x= 0,02м Оглавление Введение 1. Дифференциальное уравнение теплопроводности и условия однозначности 2. Метод конечных разностей при решении дифференциального уравнения теплопроводности. 2.1 Метод Гаусса при решении системы линейных алгебраических уравнений 2.2 Конечно разностная аппроксимация граничных условий 3. Основная часть 3.1 Исходные данные для расчета 3.2 Математическая постановка задачи 3.3 Программный код, реализующий алгоритмы расчета 3.4 Результаты расчета Список использованных источников Введение Большинство существующих способов сварки основано на нагреве материала до пластического состояния или плавления. Теплоту, необходимую для этого получают из различных источников энергии, различающихся между собой по характеру выделения теплоты, мощности, продолжительности действия и прочим признакам. Существующие эмпирические и аналитические модели протекания тепловых процессов при сварке основаны на решении дифференциального уравнения теплопроводности при условии независимости теплофизических свойств от температуры, с учетом всевозможных допущений и упрощений как свариваемых тел так и тепловых источников, что вносит неточности в расчеты. Такие модели, как правило, справедливы только для конкретных диапазонов параметров сварки, изменение которых предполагает проведение большого комплекса исследований. Применение численных методов позволяет точно воспроизвести геометрические условия однозначности, задающие размеры и форму свариваемых деталей, граничные условия, разрешать нелинейные задачи теплопроводности с учётом фазовых переходов, температурной зависимости теплофизических свойств материала. Численное моделирование процессов теплообмена в настоящее время приобретает все более значительную роль в связи с необходимостью достоверного прогноза таких процессов, экспериментальное изучение которых в лабораторных или натурных условиях очень сложно и дорого, а в некоторых случаях просто невозможно. 1. Дифференциальное уравнение теплопроводности и условия однозначности В общем случае трехмерного тела при отсутствии теплообмена с окружающим пространством общее уравнение теплопроводности имеет вид: 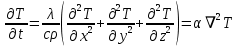 где 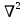 – оператор Лапласа; – оператор Лапласа; 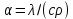 – коэффициент температуропроводности, см2/с, Т –температура или приращение температуры в точке равномерно нагретого тела. Если начальная температура тела равномерна и равна T0, то полное значение температуры Т равно T0+ΔT, где ΔT приращение температуры. – коэффициент температуропроводности, см2/с, Т –температура или приращение температуры в точке равномерно нагретого тела. Если начальная температура тела равномерна и равна T0, то полное значение температуры Т равно T0+ΔT, где ΔT приращение температуры.Решения дифференциального уравнения (1) дает разнообразные случаи распределения температуры в телах. При выводе указанных уравнений предполагалось, что коэффициенты λ, сρ и α постоянны. Для технических целей в ряде случаев точность решения оказывается достаточной, если выбирать средние значения коэффициентов диапазоне температур, характерном для рассматриваемого процесса. Уравнение (1) устанавливает связь между временным и пространственным изменением температуры в любой точке тела и описывает множество вариантов развития процессов теплопроводности. Чтобы из бесчисленного количества этих вариантов выбрать один и дать его полное математическое описание, необходимы условия однозначности, которые содержат геометрические, физические, начальные и граничные условия. Геометрические условия определяют форму и размеры тела, в котором протекает изучаемый процесс. Физические условия определяют теплофизические характеристики тела λ, ρ, с. Временные (начальные) условия содержат распределение температуры в теле в начальный момент времени:  , , 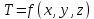 При равномерном распределении температуры в теле начальное условие упрощается: t = 0: Т = Т0= const. Граничные условия определяют особенности протекания процесса на поверхности тела и могут быть заданы несколькими способами. граничные условия первого рода – задается распределение температуры на поверхности (или границе) тела для каждого момента времени. T=Tw(x, y, z). В большинстве случаев Tw=const. граничные условия второго рода – задается значение теплового потока для каждой точки поверхности (или границы) тела в любой момент времени: 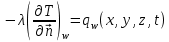 где 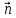 – нормаль к поверхности тела. Наиболее часто используется условие qw=const. – нормаль к поверхности тела. Наиболее часто используется условие qw=const.граничные условия третьего рода – задается взаимосвязь между потоком тепла за счет теплопроводности от твердой стенки и тепловым потоком из окружающей среды за счет температурного напора (закон Ньютона - Рихмана):  где а – коэффициент теплообмена. граничные условия четвертого рода – для определения теплового взаимодействия между элементами, имеющими различные теплофизические характеристики, задают условия равенства температур и тепловых потоков по обе стороны от границы раздела: 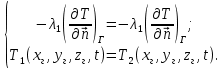 где  – координаты границы раздела сред; Т1, Т2– температуры соприкасающихся сред. – координаты границы раздела сред; Т1, Т2– температуры соприкасающихся сред. Дифференциальное уравнение вместе с условиями однозначности дает полную математическую формулировку краевой задачи теплопроводности. Для расчетов процесса распространений тепла наряду с аналитическим применяют численные методы. Твердое тело представляется в виде совокупности узлов, а дифференциальное уравнение заменяют приближенным выражением, связывающим не бесконечно малые, а небольшие конечные приращения температур времени и длины. То есть вместо производных в дифференциальном уравнении используются их конечноразностные аппроксимации. При этом получают систему линейных алгебраических уравнений для определения температуры, как локальной характеристики в каждом узле сетки. Полученная система является незамкнутой, для ее замыканию используют разностное представление граничных условий. В результате получают замкнутую систему линейных алгебраических уравнений, которую решают численными методами. 2. Метод конечных разностей при решении дифференциального уравнения теплопроводности В качестве примера рассмотрим краевую задачу на основе одномерного уравнения теплопроводности. Анализируется теплопередача через плоскую бесконечную пластину или изолированный стержень (рис. 4). На одном торце стержня поддерживается постоянная температура Тл, на другом – температура Тп. Начальная температура равна T0, источники тепловыделения внутри стержня отсутствуют. П  ри заданных условиях температура будет изменяться только в направлениях, перпендикулярных сечению стержня. Если ось Ох направить, как показано на рис. 1, то температура в направлении Оyи Оzможет считаться постоянной. Также предположим, что теплофизические характеристики не зависят от температуры. В связи с этим дифференциальное уравнение (1) преобразуется к виду: ри заданных условиях температура будет изменяться только в направлениях, перпендикулярных сечению стержня. Если ось Ох направить, как показано на рис. 1, то температура в направлении Оyи Оzможет считаться постоянной. Также предположим, что теплофизические характеристики не зависят от температуры. В связи с этим дифференциальное уравнение (1) преобразуется к виду: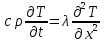 , 0 < x < L. (2) , 0 < x < L. (2)Начальные и граничные условия запишутся следующим образом: 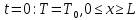 ; ;  ; (3) ; (3)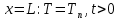 . . Для того чтобы дать полное математическое описание рассматриваемой задачи, необходимо еще задать физические условия однозначности. Эту задачу будем решать методом конечных разностей на равномерной сетке. Для этого разобьем пластину по толщине на N-1 равных промежутков, т.е. построим конечно-разностную сетку (рис. 2):  Определим значение температуры в i-м узле в момент времени t = tп=п·τ как Т(хi;, tп) = Тi". Здесь τ – шаг интегрирования по временной координат, п – номер шага по времени. Далее заменим дифференциальные операторы в (2) на их конечно-разностные аналоги. Будем пользоваться неявной схемой. 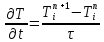 , , . .В результате аппроксимации частных производных соответствующими конечными разностями получаем следующую систему линейных алгебраических уравнений (СЛАУ): 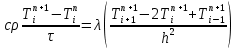 , , 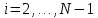 , , 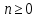 . (4) . (4)Выбранную схему аппроксимации частных производных можно графически представить следующим образом: На рис. 3 показано, что используется четырехточечная разностная схема – три точки берутся на новом временном слое и одна со старого временного слоя. С  формулированный выше способ аппроксимации производных называется неявным потому, что поле температуры на новом временном слое представлено неявно, т.е. для его определения необходимо решать систему уравнений (4). формулированный выше способ аппроксимации производных называется неявным потому, что поле температуры на новом временном слое представлено неявно, т.е. для его определения необходимо решать систему уравнений (4).2.1 Метод Гаусса при решении системы линейных алгебраических уравнений Полученную систему (4) можно свести к наиболее общему виду: 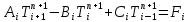 , (5) , (5)где  , ,  , , 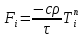 . .Такие уравнения называют трехточечными разностными уравнениями второго порядка. Система (5) имеет трехдиагональную структуру. В связи с тем, что рассматривается нестационарная задача, систему (5) необходимо решать на каждом шаге по времени. Предположим, что существуют такие наборы чисел αi и βi (i = 1,2 … N-1), при которых: 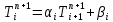 , (6) , (6)т.е. трехточечное уравнение второго порядка (5) преобразуется в двухточечное уравнение первого порядка (6). Уменьшим в связи с (6) индекс на единицу и полученное выражение 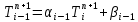 , подставим в данное уравнение (5): , подставим в данное уравнение (5): , ,откуда получаем: 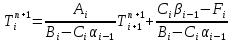 . .Последнее равенство имеет вид (6) и будет точно с ним совпадать, если при всех i = 2,3,...,N-1 выполняются соотношения:  , , 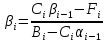 . (7) . (7)Для определения 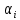 и и  необходимо знать необходимо знать  и и 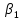 которые находятся из левого граничного условия. которые находятся из левого граничного условия.Далее по формулам (6) последовательно находятся  , при условии, что , при условии, что 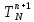 найдено из правого граничного условия. найдено из правого граничного условия.Таким образом, решение уравнений вида (5) описываемым способом, называемым методом прогонки, сводится к вычислениям по трем формулам: нахождение так называемых прогоночных коэффициентов 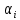 и и  по формулам (7) i = 2,3,...,N-1 (прямая прогонка) и затем получение неизвестных по формулам (7) i = 2,3,...,N-1 (прямая прогонка) и затем получение неизвестных 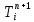 по формуле (6) при i = N-1, N-2,...,2 (обратная прогонка). по формуле (6) при i = N-1, N-2,...,2 (обратная прогонка).Для успешного применения метода прогонки нужно, чтобы в процессе вычислений не возникло ситуаций с делением на нуль, а при больших размерностях систем не должно быть быстрого роста погрешностей округлений. Будем называть прогонку корректной, если знаменатели прогоночных коэффициентов (7) не обращаются в нуль, и устойчивой, если  при всех при всех 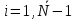 . .Возвращаясь к системе (4), определим прогоночные коэффициенты и воссоздадим полный алгоритм решения полученной системы. Поскольку при х = 0 Т = Тл, то 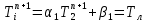 , , , , 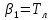 а при х = L Т = Тn 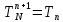 . .Прогоночные коэффициенты вычисляются по формулам (7). 2.2 Конечно разностная аппроксимация граничных условий Будем использовать неявную разностную схему, а граничные условия будут использоваться для нахождения первых прогоночных коэффициентов α1 и β1 (левое граничное условие), и температуры ТN (правое граничное условие). Граничное условие – 1-го рода:  , , 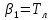 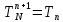 . .Граничное условие – 2-го рода:   . .Граничное условие – 3-го рода: 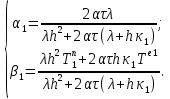  Граничное условие – 4-го рода, определяет прогоночные коэффициенты на границе раздела двух материалов: 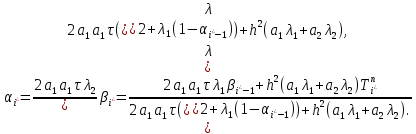 3. Основная часть 3.1 Исходные данные для расчета Рассмотрим краевую задачу на основе одномерного уравнения теплопроводности. Анализируется теплопередача через двухслоную бесконечную пластину (или изолированный стержень). Геометрия задачи показана на рис. 1. На одной стороне пластины (слева) поддерживается температураT=70°С. На другой стороне пластины (справа) задана q=0. При заданных условиях температура будет изменяться только в направлении оси Ox, теплофизические коэффициенты не зависят от температуры. 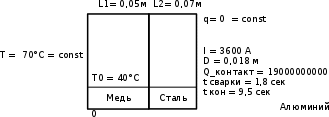 3.2 Математическая постановка задачи Запишем дифференциальные уравнения описывающие процесс теплопередачи в пластине: 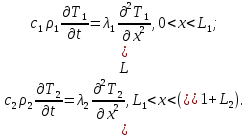 Начальные и граничные условия запишем следующим образом  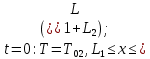 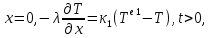  . .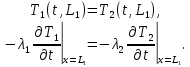 Код программы : Private Sub CommandButton1_Click() Const mf = 1000 Const pi = 3.141592 Dim T(1 To mf) As Double Dim Tt(1 To mf) As Double Dim alfa(1 To mf) As Double Dim beta(1 To mf) As Double Dim i, j, N As Double Dim ai, bi, ci, fi As Double Dim lamda1, ro1, c1, a1, h, tau, d, Isv, Sd, p_ud1, p_ud2, Q_contact As Double Dim lamda2, ro2, c2, a2 As Double Dim T0, Tr, L1, L2, t_end, time As Double Dim left, right, Ng As Integer Dim T1, q1, Te1, k1, Qintern1, Qintern As Double Dim T2, q2, Te2, k2, Qintern2 As Double N = CSng(TextBox1.Text) t_kon = CSng(TextBox2.Text) t_svar = CSng(TextBox29.Text) L1 = CSng(TextBox21.Text) L2 = CSng(TextBox22.Text) lamda1 = CSng(TextBox4.Text) ro1 = CSng(TextBox5.Text) c1 = CSng(TextBox6.Text) lamda2 = CSng(TextBox20.Text) ro2 = CSng(TextBox18.Text) c2 = CSng(TextBox19.Text) T0 = CSng(TextBox7.Text) T1 = CSng(TextBox10.Text) T2 = CSng(TextBox12.Text) Te1 = CSng(TextBox15.Text) Te2 = CSng(TextBox14.Text) q1 = CSng(TextBox11.Text) q2 = CSng(TextBox13.Text) k1 = CSng(TextBox16.Text) k2 = CSng(TextBox17.Text) d = CSng(TextBox25.Text) Isv = CSng(TextBox24.Text) a1 = lamda1 / (c1 * ro1) a2 = lamda2 / (c2 * ro2) Sd = pi * d ^ 2 / 4 j = Isv / Sd p_ud1 = CSng(TextBox27.Text) p_ud2 = CSng(TextBox26.Text) Qintern1 = p_ud1 * j ^ 2 Qintern2 = p_ud2 * j ^ 2 Q_contact = CSng(TextBox28.Text) 'шаг сетки по пространственной координате h = (L1 + L2) / (N - 1) Ng = L1 / h 'расчетный шаг сетки по времени tau = t_kon / 100 'Определяем поле температур в начальный момент времени For i = 1 To N T(i) = T0 Next i If OptionButton1.Value = True Then left = 1 End If If OptionButton2.Value = True Then left = 2 End If If OptionButton3.Value = True Then left = 3 End If If OptionButton4.Value = True Then right = 1 End If If OptionButton5.Value = True Then right = 2 End If If OptionButton6.Value = True Then right = 3 End If 'Интегрируем нестационарное уравнение теплопроводности time = 0 Dim time_i As Integer time_i = 0 While time < t_kon time = time + tau time_i = time_i + 1 If time > t_svar Then Q_contact = 0 Qintern = 0 Qintern1 = 0 Qintern2 = 0 End If 'Определяем начальные прогоночные коэффициенты на основе левого граничного условия Select Case left Case 1 alfa(1) = 0 beta(1) = T1 Case 2 alfa(1) = (2 * a1 * tau) / (h ^ 2 + 2 * a1 * tau) beta(1) = (h ^ 2 / (h ^ 2 + 2 * a1 * tau)) * T(1) + (2 * a1 * tau * h * q1) / lamda1 * (h ^ 2 + 2 * a1 * tau) Case 3 alfa(1) = (2 * a1 * tau * lamda1) / (lamda1 * h ^ 2 + 2 * a1 * tau * (lamda1 + h * k1)) beta(1) = (lamda1 * h ^ 2 * T(1) + 2 * a1 * tau * h * k1 * Te1) / (lamda1 * h ^ 2 + 2 * a1 * tau * (lamda1 + h * k1)) End Select 'Определяем прогоночные коэффициенты For i = 2 To Ng - 1 If i = Ng - 1 Then Qintern = Q_contact Else Qintern = Qintern1 End If ai = lamda1 / h ^ 2 bi = 2 * lamda1 / h ^ 2 + ro1 * c1 / tau ci = lamda1 / h ^ 2 fi = -ro1 * c1 * T(i) / tau - Qintern alfa(i) = ai / (bi - ci * alfa(i - 1)) beta(i) = (ci * beta(i - 1) - fi) / (bi - ci * alfa(i - 1)) Next i alfa(Ng) = 2 * a1 * a2 * tau * lamda2 / (2 * a1 * a2 * tau * (lamda2 + lamda1 * (1 - alfa(Ng - 1))) + h ^ 2 * (-a1 * lamda1 + a2 * lamda2)) beta(Ng) = (2 * a1 * a2 * tau * lamda1 * beta(Ng - 1) + h ^ 2 * (-a1 * lamda1 + a2 * lamda2) * T(Ng)) / (2 * a1 * a2 * tau * (lamda2 + lamda1 * (1 - alfa(Ng - 1))) + h ^ 2 * (-a1 * lamda1 + a2 * lamda2)) For i = Ng + 1 To N - 1 ai = lamda2 / h ^ 2 bi = 2 * lamda2 / h ^ 2 + ro2 * c2 / tau ci = lamda2 / h ^ 2 fi = -ro2 * c2 * T(i) / tau - Qintern2 alfa(i) = ai / (bi - ci * alfa(i - 1)) beta(i) = (ci * beta(i - 1) - fi) / (bi - ci * alfa(i - 1)) Next i 'Определяем значение температуры на правой границе Select Case right Case 1 T(N) = T2 Case 2 T(N) = (2 * a2 * tau * lamda2 * beta(N - 1) - 2 * a2 * tau * h * q2 + h ^ 2 * lamda2 * T(N)) / (lamda2 * h ^ 2 + 2 * a2 * tau * lamda2 * (1 - alfa(N - 1))) Case 3 T(N) = (lamda2 * h ^ 2 * T(N) + 2 * a2 * tau * (lamda2 * beta(N - 1) + h * k2 * Te2)) / (lamda2 * h ^ 2 + 2 * a2 * tau * (h * k2 + lamda2 * (1 - alfa(N - 1)))) End Select 'Определяем поле температур For i = (N - 1) To 1 Step -1 T(i) = alfa(i) * T(i + 1) + beta(i) Next i Tt(time_i) = T(Ng - 1) Wend 'Записываем результаты T(i) в таблицу Dim S As String 'пользовательская переменная Dim v_Excel As Excel.Application 'область памяти приложения Excel Dim v_Wb1 As Excel.Workbook 'область рабочей книги Dim sh As Excel.Worksheet 'область рабочего листа Set v_Excel = New Excel.Application 'Открываем новое приложение Excel 'Загружаем рабочую книгу Set v_Wb1 = v_Excel.Workbooks.Open("I:temp.xlsx") Set sh = v_Excel.Sheets(1) 'Загружаем рабочий лист 1 v_Wb1.Activate 'Получаем доступ к рабочей книге For i = 1 To N sh.Cells(i, 1).Value = (i - 1) * h sh.Cells(i, 2).Value = T(i) Next i For i = 1 To 100 sh.Cells(i, 3).Value = (i - 1) * tau sh.Cells(i, 4).Value = Tt(i) Next i v_Excel.Quit 'Закрытие приложения Excel Set v_Excel = Nothing End Sub   Список используемых источниковСамарский А. А., Вабищевич П. Н. Вычислительная теплопередача. - М.: Едиториал УРСС, 2003. – 782 с. Самарский А. А. Теория разностных схем. – М.: Наука, 1977. – 656 с. Волков Е. А. Численные методы. – М.: Наука, 1987. – 248 с. Вержбицкий В. М. Основы численных методов. – М.: Высшая школа, Лыков А. В. Теория теплопроводности. – М.: Высшая школа, 1967. – 600 с. |
