Лекция-9. IX. движение границы раздела двух жидкостей в пористой среде кинематические условия на подвижной границе раздела при взаимном вытеснении жидкостей
 Скачать 0.78 Mb. Скачать 0.78 Mb.
|
|
IX. ДВИЖЕНИЕ ГРАНИЦЫ РАЗДЕЛА ДВУХ ЖИДКОСТЕЙ В ПОРИСТОЙ СРЕДЕ 1. Кинематические условия на подвижной границе раздела при взаимном вытеснении жидкостей Задачи о движении границы раздела двух жидкостей в пористой среде представляют большой теоретический и практический интерес. Так при разработке нефтяных месторождений в условиях водонапорного режима наблюдается стягивание контура нефтеносности под напором грунтовых вод. Аналогичная задача о движении границы раздела двух жидкостей с различными физическими свойствами (вязкостью и плотностью) возникает в некоторых случаях и при разработке газовых месторождений c активной краевой или подошвенной водой. Строгое гидродинамическое решение задачи о движении границы раздела двух жидкостей, пригодное для практических расчетов, отсутствует. Исследованы лишь отдельные, частные случаи; разработаны некоторые приближенные методы. Основная трудность точного решения задачи о движении границы раздела двух жидкостей в пористой среде заключается в том, что на границе раздела двух жидкостей происходит преломление линий тока. Пусть кривая I-I (рис. 56) является границей раздела двух жидкостей с вязкостями 1 и 2 и пусть 2>1 (нефть-2 вытесняется водой-1). 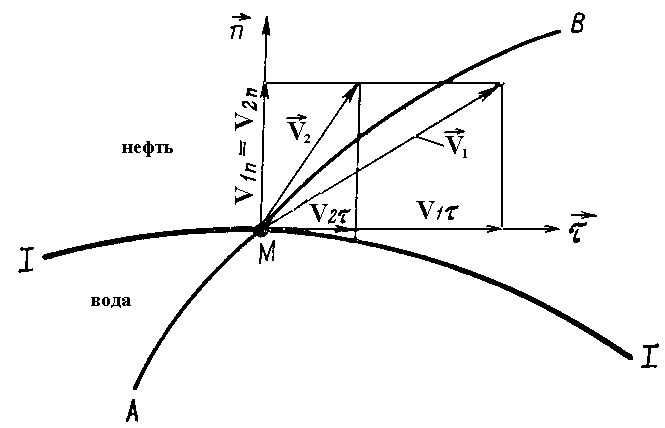 Рис. 56 Рассмотрим произвольную точку М границы I-I и проведем через нее касательную Так как 2>1, то из (9.1) следует, что Следовательно, линии тока АМ и МВ, проходящие через точку М, будут иметь излом в точке М. Учет этого преломления линий тока на границе раздела жидкостей и составляет главную трудность в точном решении задачи продвижения границы раздела. Линии тока не будут преломляться только в двух случаях: при прямолинейно-параллельном и плоскорадиальном движениях границы раздела, когда 2. Прямолинейно-параллельное вытеснение нефти водой. При поршневом вытеснении нефти водой в пористой среде плотность нефти и воды будем считать одинаковыми. Это позволит рассматривать плоскость контакта нефти и воды вертикальной; при этом вязкости нефти 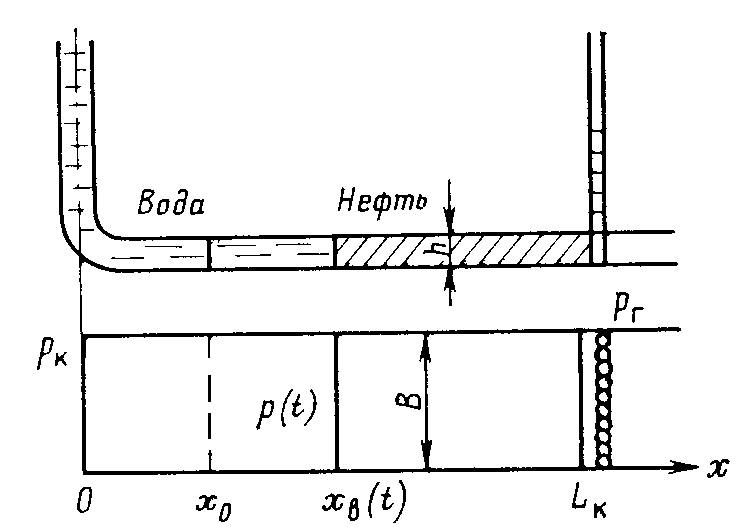 Рис. 57 Принимаем: на контуре питания и на галерее поддерживаются собственно постоянные давления РК и РГ ; начальное положение контура нефтеносности Х0 параллельно галерее и контуру питания; коэффициент пористости m = const; площадь сечения пласта РВ, РН - соответственно давление в любой точке водоносной и нефтеносной части пласта; Р(t) - давление на границе вытеснения ХВ(t); LK - расстояние от контура питания до галереи. Ранее отмечалось, что в случае прямолинейно-параллельного потока одной жидкости распределение давления Р(х) и скорость фильтрации описывались уравнениями (3.12) и (3.15): При этом изобарами являются линии, параллельные галерее и каждую изобару можно рассматривать как контур питания или как галерею. На основании формул (9.2) и (9.3) для водоносной области можно записать : Принимая за контур питания изобару, совпадающую с границей раздела жидкостей, для нефтеносной области можно записать : Найдем давление Р(t) на границе раздела. Вследствие несжимаемости жидкостей и неразрывности потока линии тока будут параллельны оси Х и не имеют преломления, а скорость фильтрации во всех точках пласта одинакова; поэтому приравниваем (9.5) и (9.7) , т.е. имеем 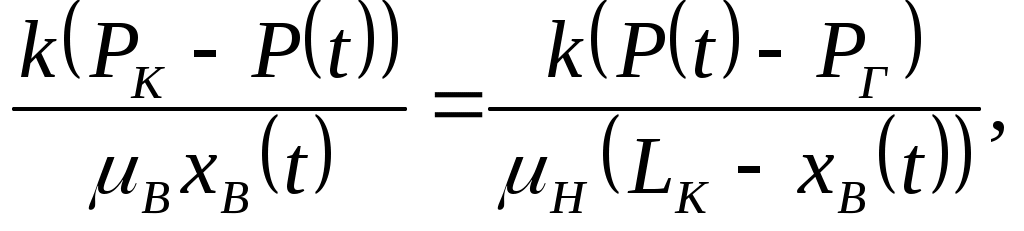 откуда давление на границе раздела будет 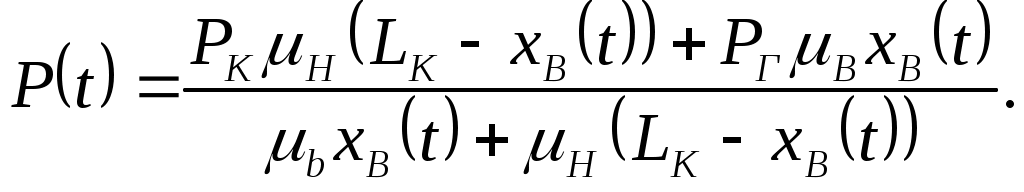 (9.8) (9.8)Далее определим основные характеристики фильтрационного потока нефти и воды. 1) Распределение давления в водоносной и нефтеносной областях. Для этого подставим (9.8) в (9.4) и (9.6): 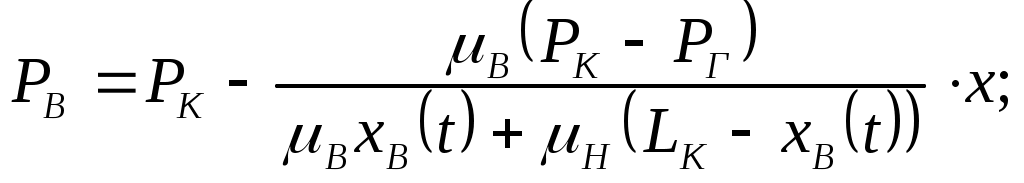 (9.9) (9.9)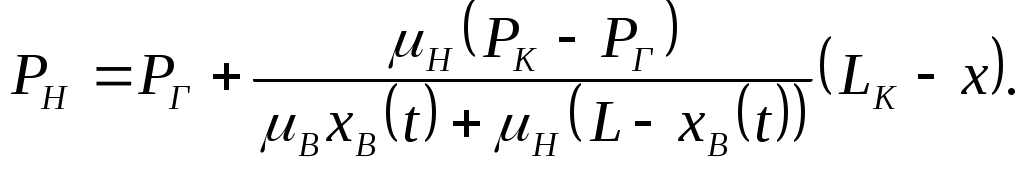 (9.10) (9.10)Из уравнений (9.9) и (9.10) видно, что давление в пласте зависит не только от координаты Х, но и от положения границы раздела ХВ, которая перемещается , т.е. ХВ(t) растет; поэтому давление в водоносной области РВ(t) падает, а в нефтеносной РН (t) растет (рис.58). Пьезометрическая линия на границе раздела имеет излом. 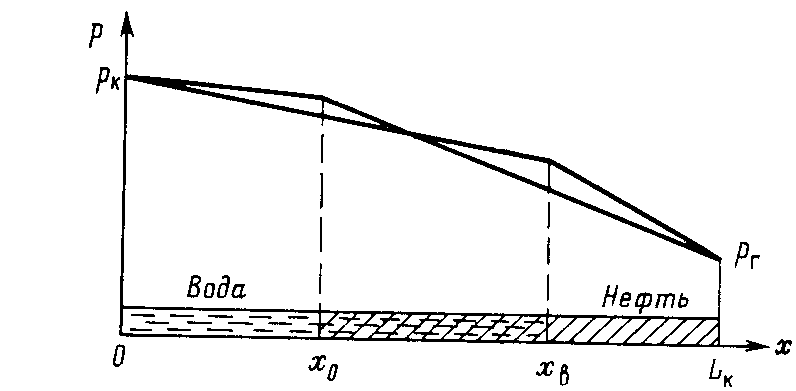 Рис. 58 2) Найдем выражение скорости фильтрации. Подставим (9.8) в (9.5) и в (9.7); получим: 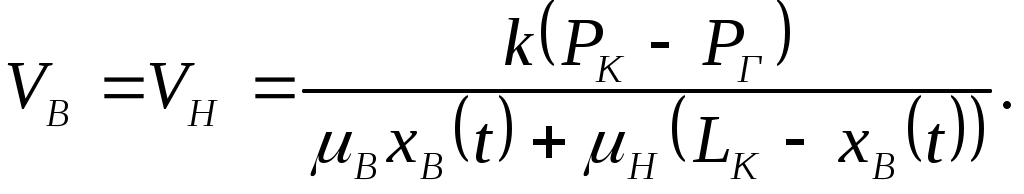 (9.11) (9.11)3) Расход жидкости (дебит галереи) Q. 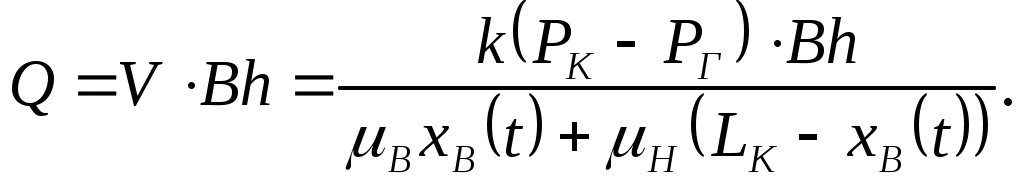 (9.12) (9.12)Как видно из (9.11) и (9.12) скорость фильтрации и расход Q жидкости также изменяются со временем. Следовательно, несмотря на постоянство депрессии 4) Градиент давления. Продифференцируем выражения (9.9) и (9.10) по координате х: 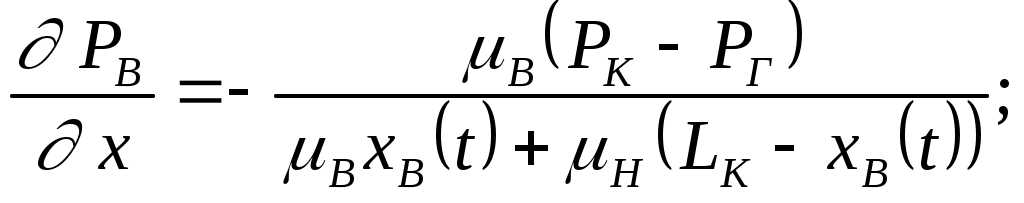 (9.13) (9.13)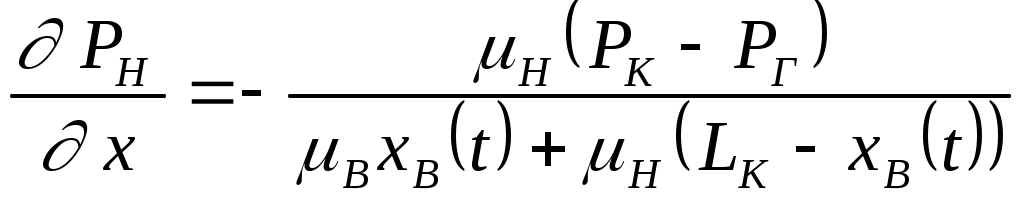 . (9.14) . (9.14)Как видно из (9.13) и (9.14), градиенты давлений в водоносной и нефтеносной областях со временем ( ХВ(t) растет) увеличиваются (линии на графике становятся более крутыми); при этом легко видеть из (9.13) и (9.14), что в нефтеносной области градиент давления больше, чем в водоносной во столько раз, во сколько Н больше В. 5) Закон движения границы раздела ХВ(t) находим из соотношения скорости фильтрации и средней скорости движения: откуда 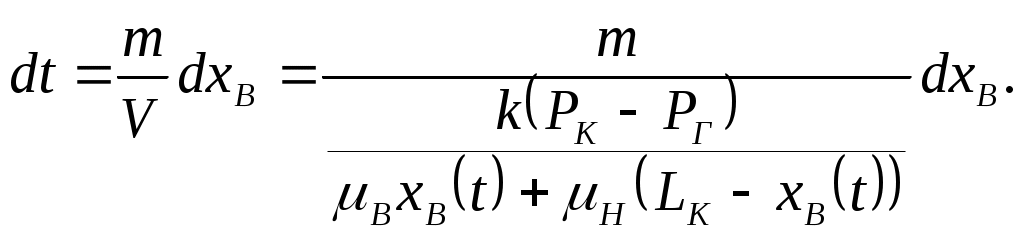 Проинтегрировав в пределах: от 0 до t и от Х0 до ХВ, получим Найдем время Т полного вытеснения нефти, полагая в (9.15) Решая квадратное уравнение (9.15), находим закон движения границы раздела: 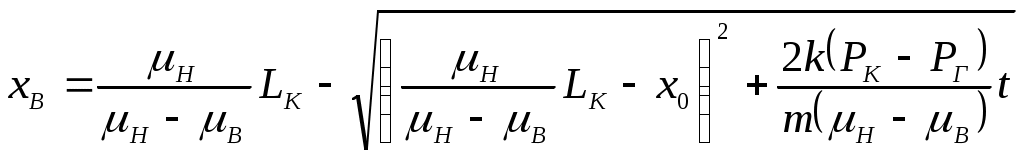 . (9.17) . (9.17)Если подставить 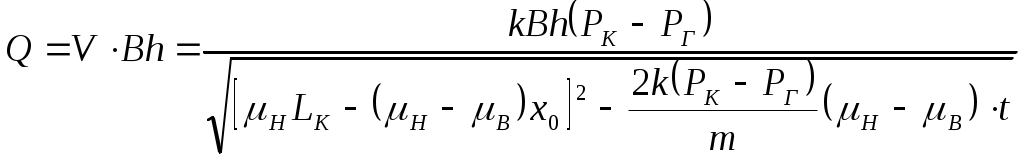 (9.18) (9.18)3. Плоскорадиальное вытеснение нефти водой Рассмотрим задачу о вытеснении нефти водой в условиях плоскорадиального движения по закону Дарси (рис.59). На контуре питания радиуса RK давление РК = const; на забое скважины радиуса rС давление РС = const; коэффициент проницаемости k = const; толщина пласта h = const. Обозначим: R0 и rH - соответственно начальное и текущее положение контура нефтеносности; PB и PH - давление в любой точке водоносной и нефтеносной области соответственно; P(t) - давление на границе раздела. 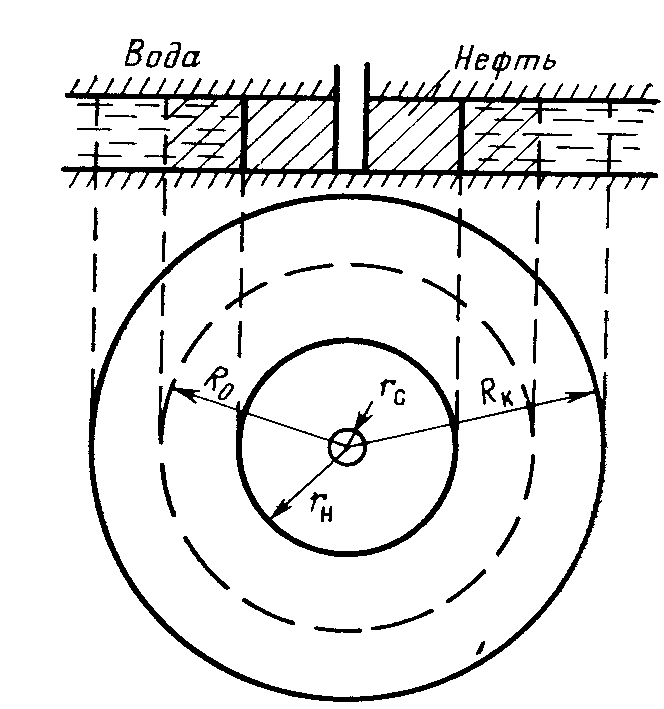 Рис. 59 В случае установившегося плоскорадиального движения однородной жидкости распределение давления в потоке и скорость фильтрации описываются следующими уравнениями (3.25) и (3.27): 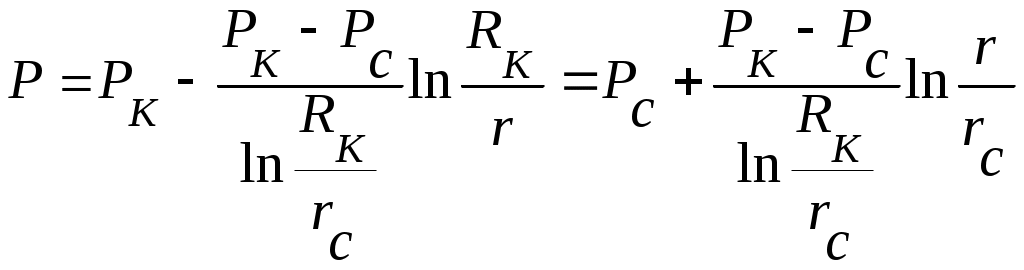 ; (9.19) ; (9.19)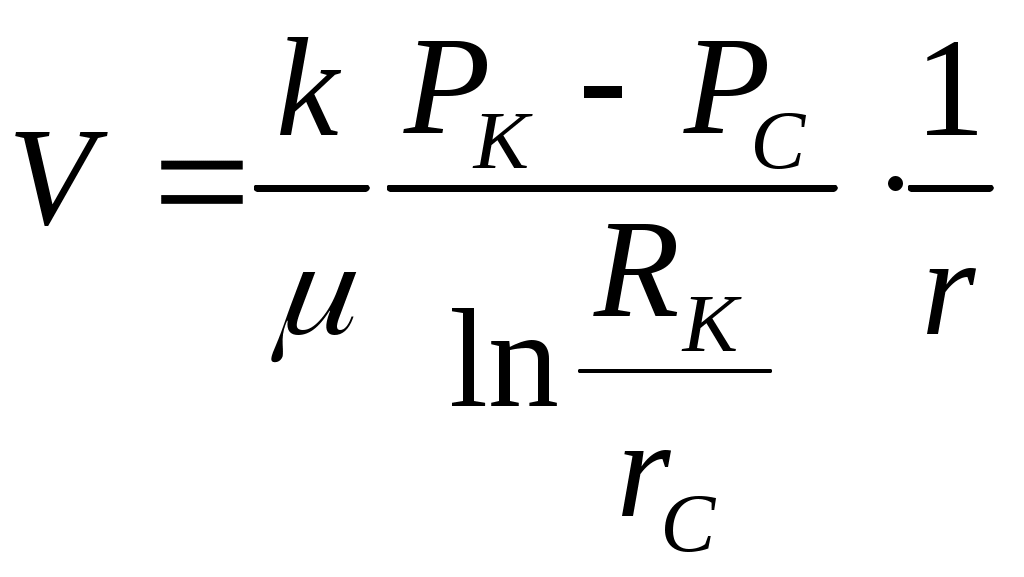 . (9.20) . (9.20)Если изобару, совпадающую в данный момент с контуром нефтеносности, принять за скважину, то распределение давления и скорость фильтрации в водоносной области можно выразить так: 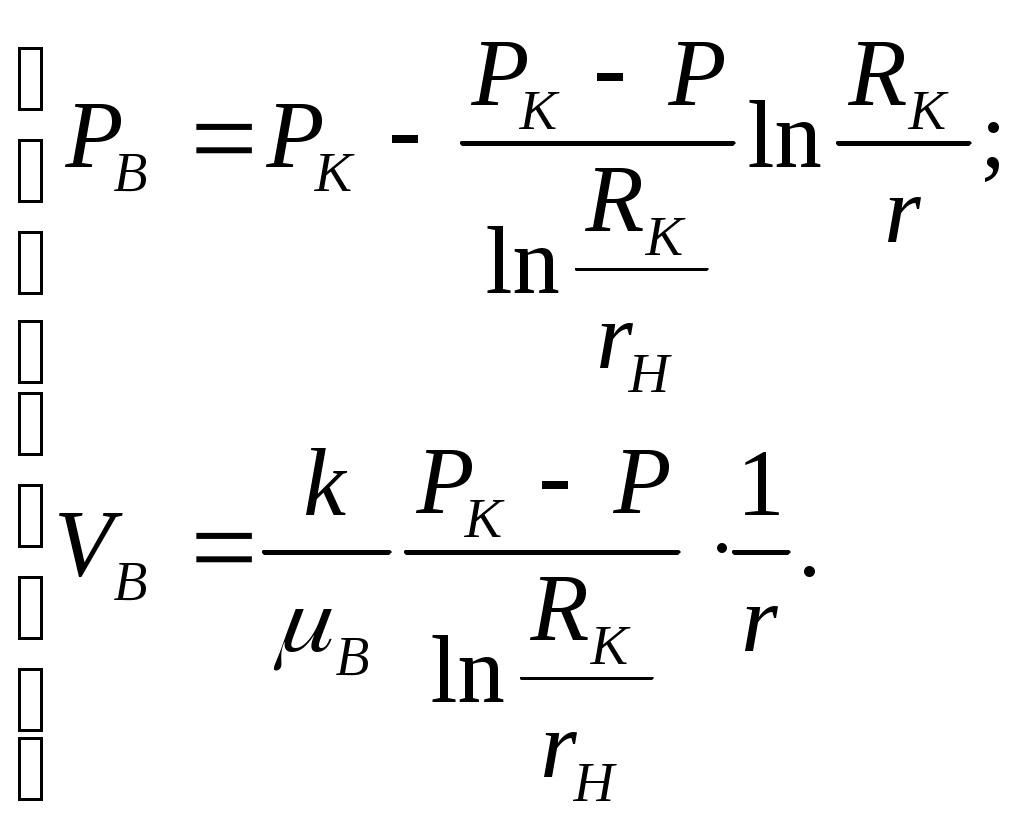 (9.21) (9.22) Теперь принимаем изобару, совпадающую с rH, за контур питания, тогда PH и VH можно записать так: 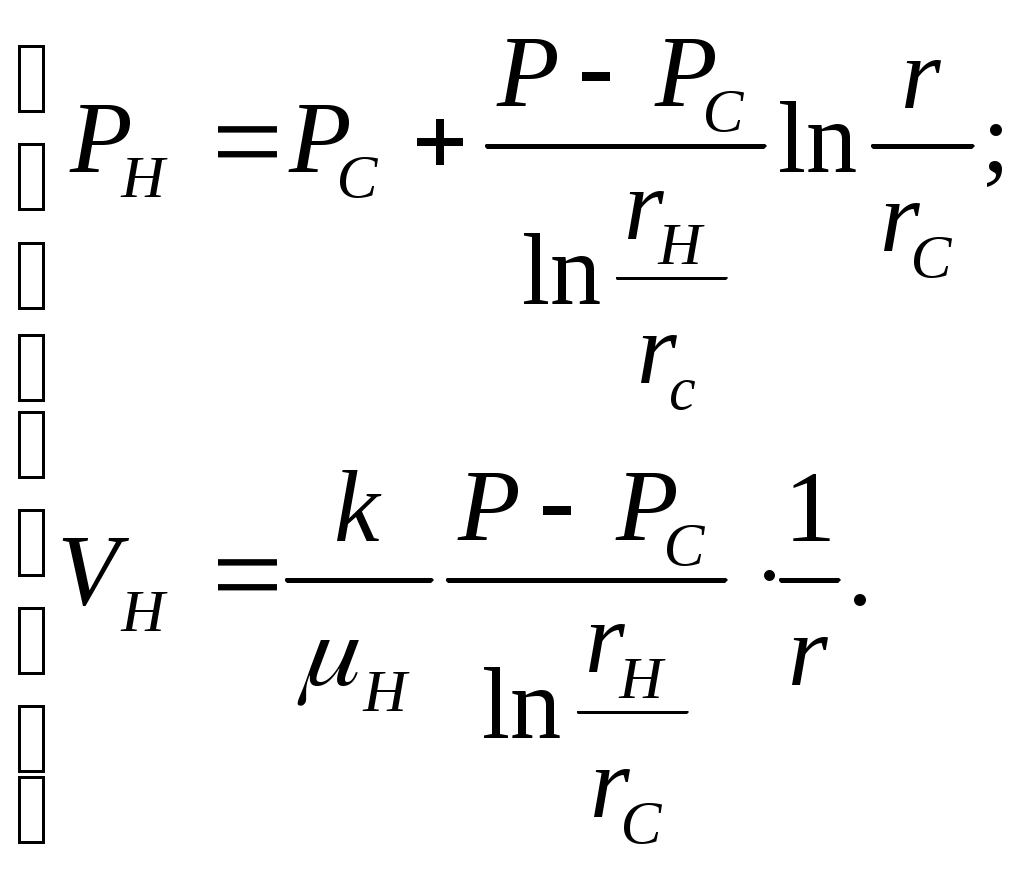 (9.23) (9.24) Давление на границе раздела двух жидкостей Р найдем из условия равенства VB=VH (при этом r = rH ).Получим: 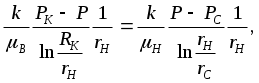 откуда 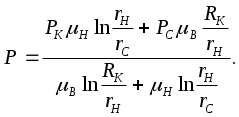 (9.25) (9.25)Рассмотрим характеристики рассматриваемого плоскорадиального фильтрационного потока нефти и воды. Распределение давления в водоносной и нефтеносной областях находим из (9.21) и (9.23), используя (9.25). Имеем: 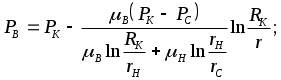 (9.26) (9.26)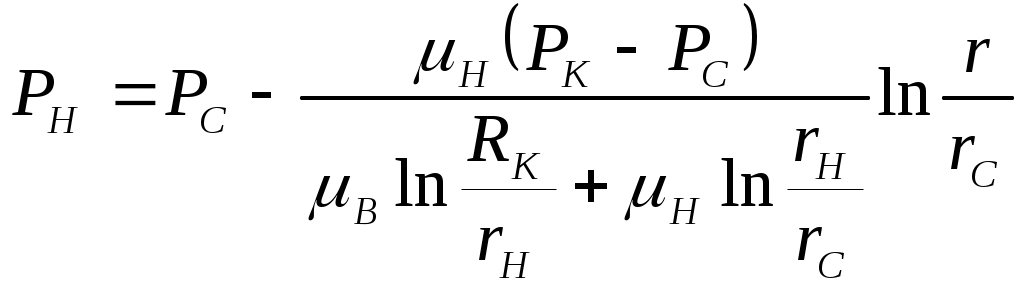 . (9.27) . (9.27)Из формул (9.26) и (9.27) видно, что закон распределения давления в обеих зонах логарифмический. Если знаменатель в (9.26) и (9.27) представить в виде 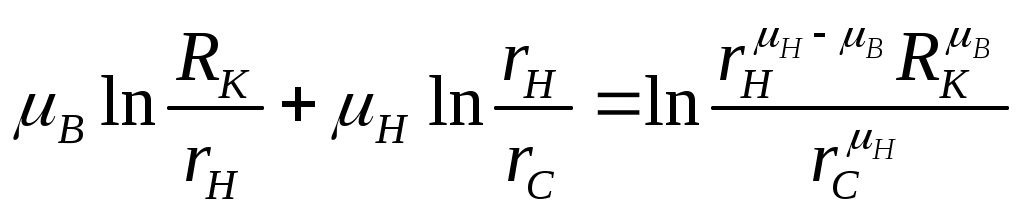 , , то можно заметить, что при rН , уменьшающемся во времени (при стягивании контура нефтеносности), этот знаменатель также уменьшается. Тогда из (9.26) и (9.27) следует, что давление в водоносной части пласта со временем уменьшается, а в нефтеносной - растет. Градиент давления в обеих частях потока найдем, продифференцировав выражения (9.26) и (9.27): 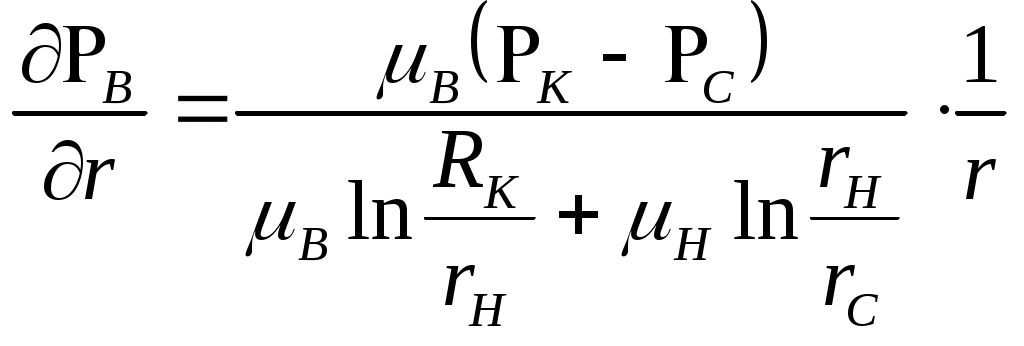 ; (9.28) ; (9.28)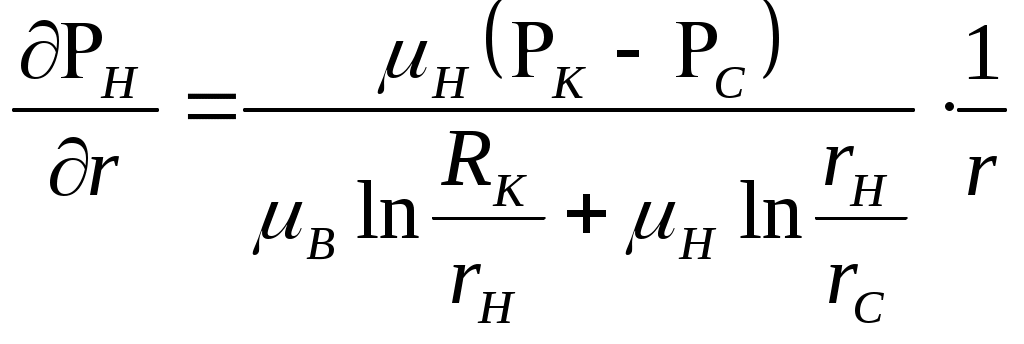 . (9.29) . (9.29)Из (9.28) и (9.29) видно, что градиенты давлений как в водоносной, так и в нефтеносной зонах растут во времени (т.к. знаменатель в этих формулах во времени уменьшается). На границе раздела жидкостей ( r = rН) градиент давления в водоносной области меньше, чем в нефтеносной во столько раз, во сколько Скорости фильтрации жидкостей определим из закона Дарси: Подставив в (9.30) значения градиентов из (9.28) и (9.29), получим: 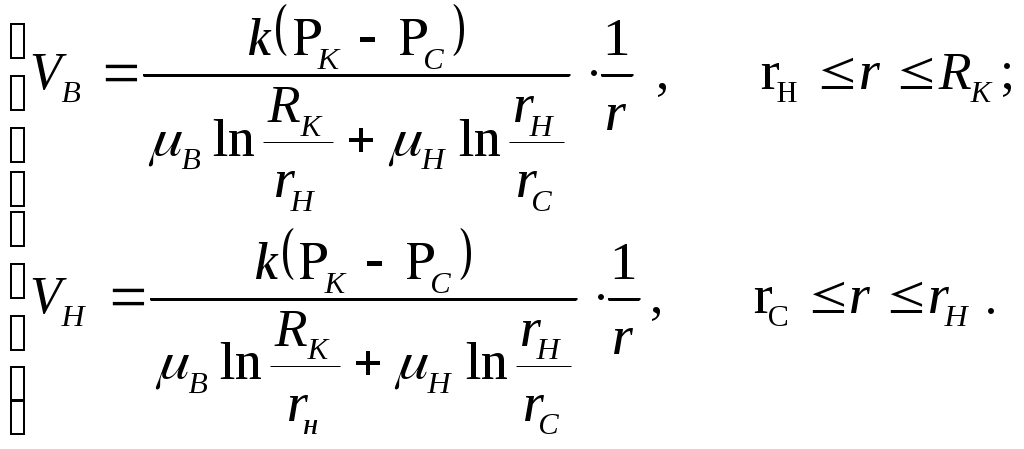 (9.31) (9.31)Из выражений (9.31) видно, что скорости фильтрации как воды, так и нефти растут со временем (знаменатель во времени уменьшается). Дебит скважины Q найдем через скорость фильтрации и площадь сечения пласта 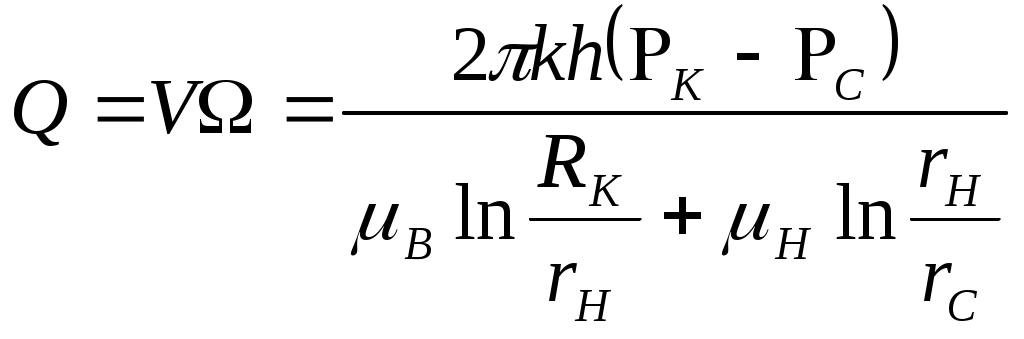 . (9.32) . (9.32)При постоянной депрессии Закон движения границы раздела жидкостей найдем из соотношения откуда Интегрируя последнее выражение в пределах от 0 до t и от 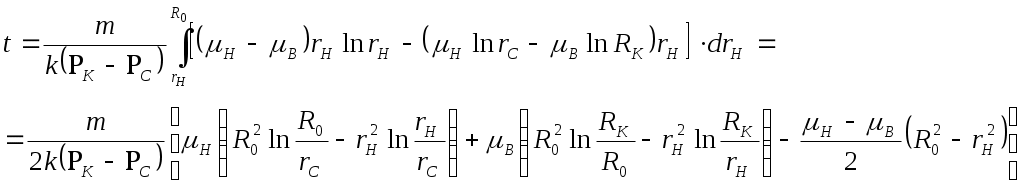 (9.33) Время вытеснения всей нефти водой Т найдем, подставив в (9.33) 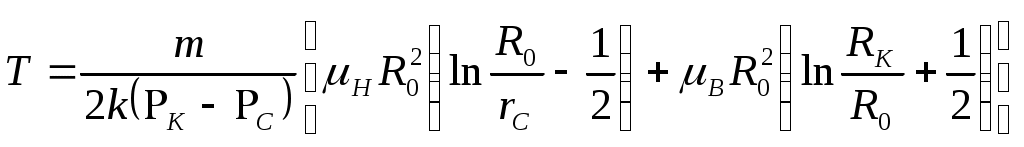 . (9.34) . (9.34)4. Устойчивость границы раздела двух жидкостей В реальных условиях движение границы раздела жидкостей значительно сложнее принятой выше модели. Обычно продуктивные пласты наклонны и граница раздела жидкостей, имеющая горизонтальное начальное положение, в процессе разработки месторождения деформируется (рис.60); перемещаясь, занимает последовательно положения A1B1, A2B2 и т.д. 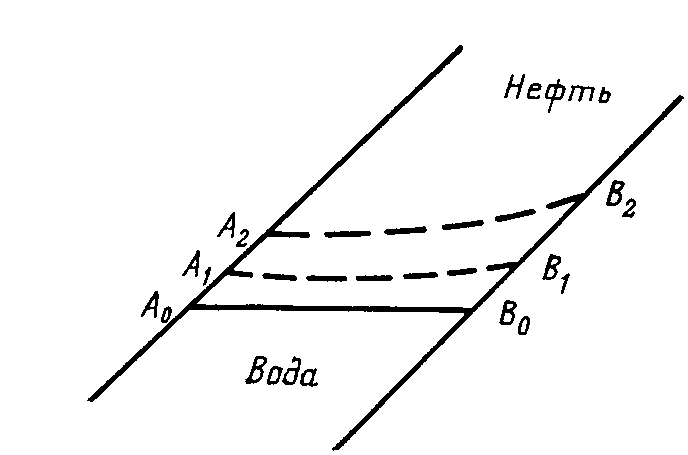 Рис. 60 Рассмотрим вопрос об устойчивости движения границы раздела. Если частица вытесняющей жидкости (вода), попавшая в область, занятую вытесняемой жидкостью (нефтью), замедляет свое движение, такое движение границы называется устойчивым, при ускорении последующего движения - процесс движения границы является неустойчивым. Условие устойчивости движения границы раздела можно установить следующим образом. Запишем выражения скоростей фильтрации для каждой жидкости согласно закону Дарси с учетом силы тяжести Запишем выражение скорости фильтрации воды, попавшей в поток нефти - В свою очередь скорость фильтрации основных частиц нефти, соприкасающихся с проникшими туда частицами воды, согласно второму уравнению из (9.35) будет Из выражений (9.36) и (9.37) можно найти связь между скоростями фильтрации откуда Об устойчивости же движения границы раздела можно судить по разности скоростей фильтрации 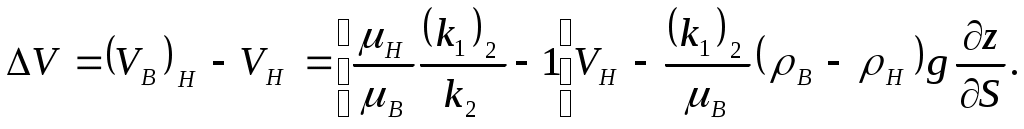 (9.38) (9.38)При при Если угол наклона пласта к горизонту обозначить через 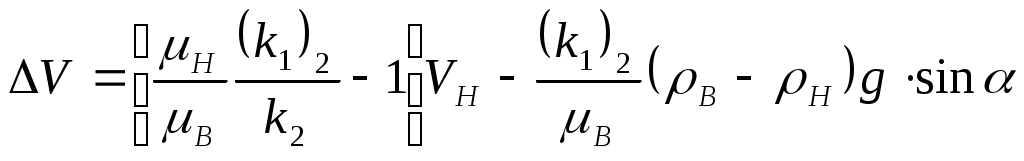 . (9.39) . (9.39)Обычно Так как при устойчивом движении границы раздела Движение всегда устойчиво при малых скоростях Когда 5. Основы теории конусообразования; предельный безводный и безгазовый дебит скважины В пологозалегающих пластах с очень малым углом наклона к горизонту площадь водонефтяного контакта очень велика, а поэтому с самого начала эксплуатации скважины оказываются в нефтяном пласте с подошвенной водой. При отборе нефти поверхность водонефтяного контакта деформируется и принимает вид холма. Такой водонефтяной холм называется конусом подошвенной воды. Если повысить депрессию и отбор нефти, то вода прорвется в скважину и скважина будет давать нефть вместе с водой. Точной теории конусообразования не существует ввиду сложности решения самой математической задачи в ее строгой постановке. Приближенная теория этого явления, выдвинутая Маскетом-Чарным, позволяющая рассчитать предельный безводный дебит и депрессию, исходит из допущения, что отклонение поверхности раздела двух фаз от первоначальной плоской формы не влияет на распределение потенциала скоростей фильтрации в нефтяной части пласта. Р 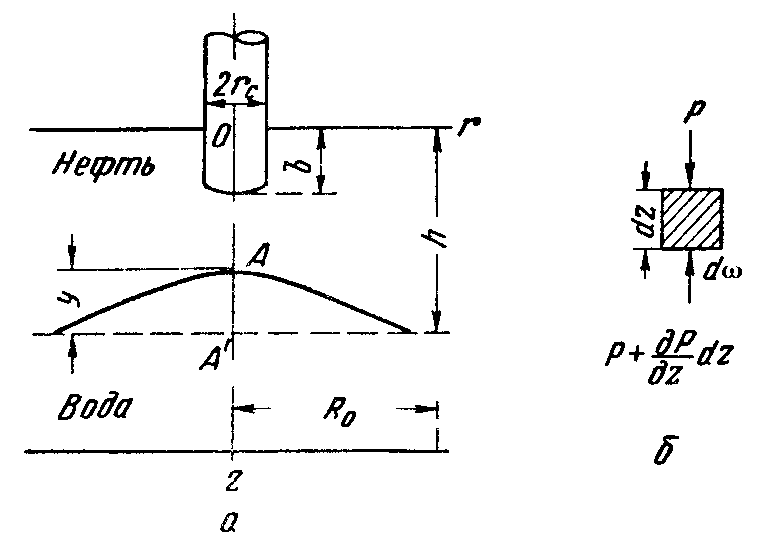 ассмотрим задачу о притоке нефти к скважине, несовершенной по степени вскрытия, но совершенной по характеру вскрытия в изотропном пласте при устойчивом неподвижном конусе подошвенной воды. Движение считаем следующим закону Дарси; кровля, подошва и первоначальная поверхность раздела принимаются горизонтальными. Режим пласта водонапорный; действием капиллярных сил пренебрегаем. (рис. 61). Рис.61 Прежде всего выясним условия, при которых частицы воды на поверхности конуса будут неподвижными. Предположим, что распределение давления в любой точке пласта известно, т.е. известна функция Р=Р(r,z). (давление как таковое, а не приведенное). Выделим на вершине конуса (r=0) элементарный объем жидкости (цилиндрик) площадью сечения d, высотой dz и рассмотрим действующие на него силы (полагая, что этот объем попал в нефтяную часть). Давление на верхнюю грань Р=Р(0;z); давление на нижнюю грань Р/=Р(0;z+dz)=P+dP=P+ Составим уравнение равновесия сил, действующих на нашу частицу (элементарный объем) воды. Сила, действующая на частицу вверх, будет равна: Сила, действующая на частицу вниз (сила тяжести): Условие устойчивости элементарного объема воды будет иметь вид или Переходя от давления к потенциалу получаем условие устойчивости (9.42) в виде Выясним как распределяется потенциал вдоль границы раздела. Согласно формуле (9.43) потенциал вдоль границы раздела равен Условие статического равновесия границы раздела (т. А) выражается формулой где Подставляя значения из (9.46) в (9.45) и замечая, что есть потенциал на контуре питания R0 при z=h, получаем окончательно т.е. вдоль границы раздела текущей нефти и неподвижной воды потенциал изменяется линейно. Распределение потенциала вдоль границы раздела текущей нефти - неподвижной воды, вдоль оси скважины и цилиндрической поверхности R0 , представлен на рис. 62. 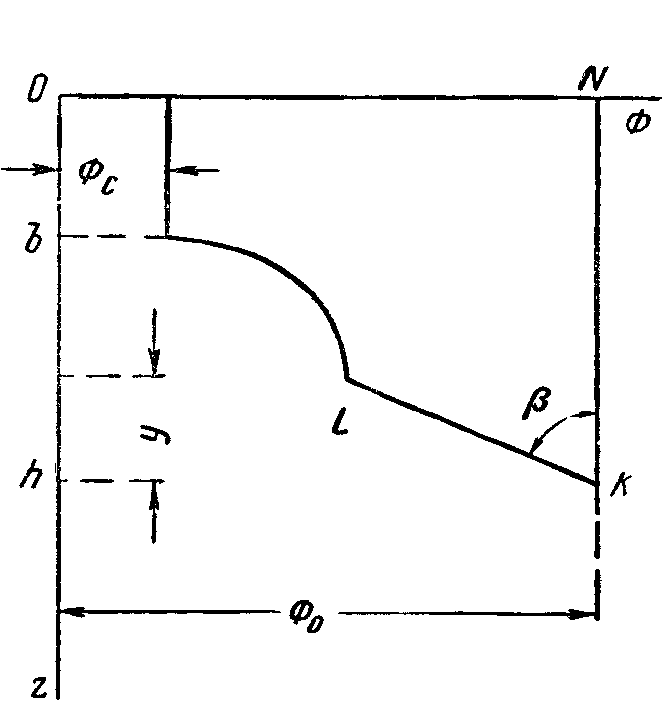 Рис.62Анализируя распределение потенциала вдоль стенки несовершенной скважины и вдоль оси z невскрытой части пласта при невозмущенном и возмущенном (при наличии конуса воды) движение нефти, И.А. Чарный установил точное соотношение, в пределах которого находится истинный предельный безводный дебит: Вычисляя дебиты Q1 и Q2 по формулам для известного решения задачи о напорном притоке к несовершенной скважине в пласте постоянной толщины, можно количественно оценить значения Q1 и Q2. Расчеты показывают, что верхние и нижние значения предельного дебита (Q1 и Q2) различаются в среднем на 25-30%. Все сказанное выше полностью распространяется на случай прорыва верхнего газа при наличии газовой шапки; при этом под Для практических расчетов используются универсальные графики зависимости безразмерного дебита 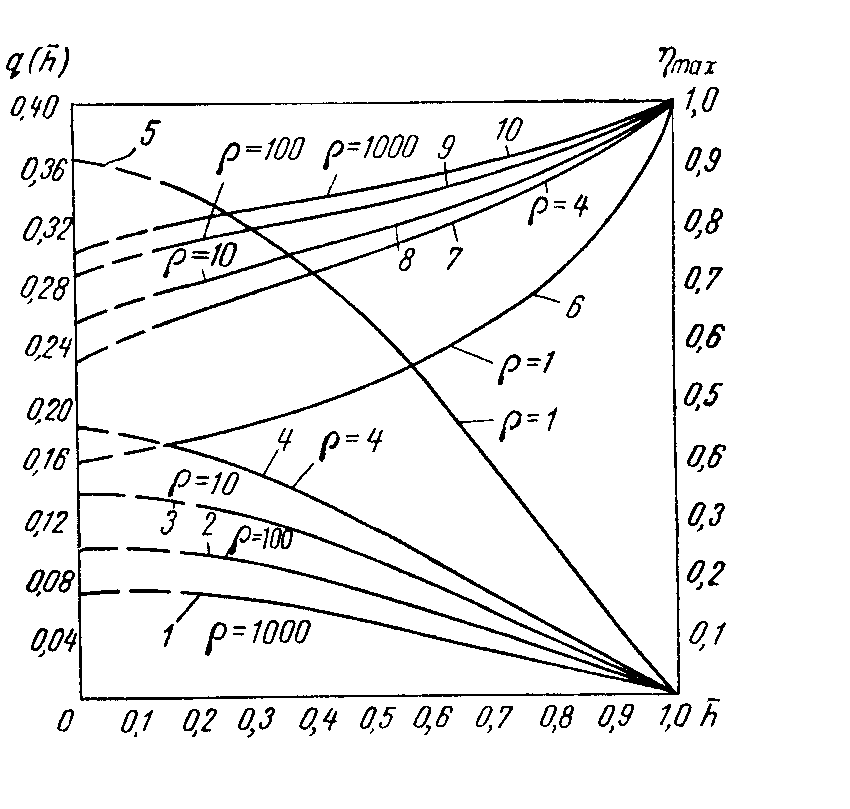 Рис.63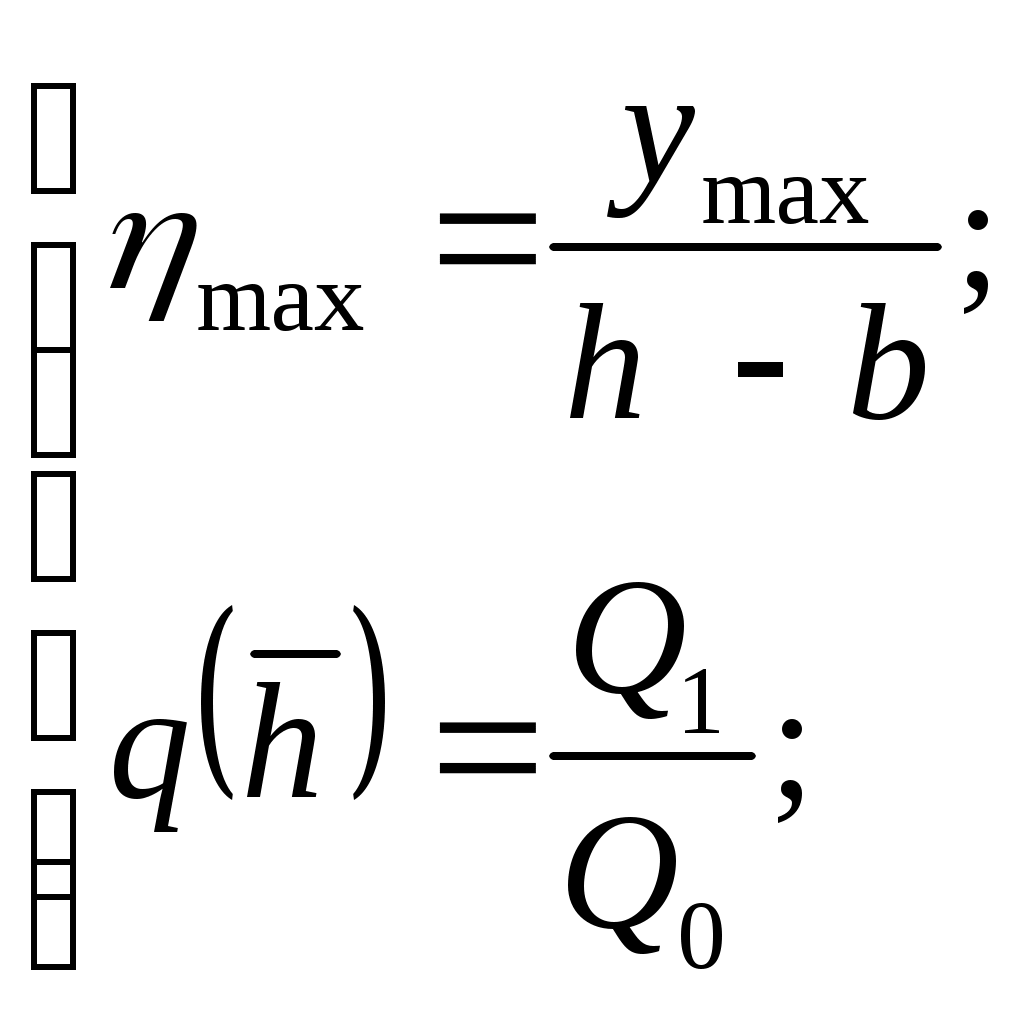 Из графиков видно, что при малых Заметим, что величина предельного дебита практически не зависит от конструкции скважины; предельная же депрессия зависит существенно от конструкции скважины и характера вскрытия пласта. Приведенные выше графики практически также можно использовать для расчетов в пластовых условиях предельных безводных дебитов несовершенных газовых скважин с подошвенной водой. |
