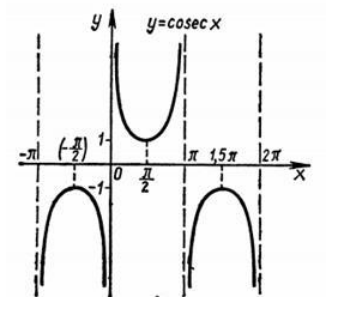
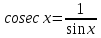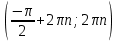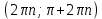Реферат, элементарные функции. Федеральное государственное автономное. Реферат по дисциплине Высшая математика На тему Функции Студент первого курса дневного отделения
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
|
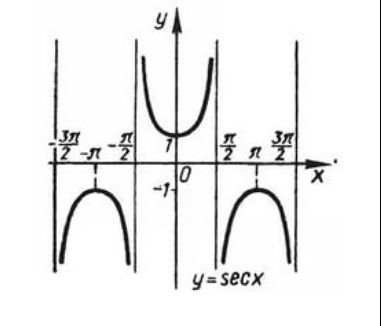
Федеральное государственное автономное образовательное учреждение высшего образования «CАНКТ - ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Институт Электроники и Телекоммуникаций Кафедра высшей математики РЕФЕРАТ По дисциплине: «Высшая математика» На тему: «Функции» Выполнил: Студент первого курса дневного отделения группы №4931601/20002 Трубинов Д.Е. Проверила: Доцент Единова Е.С. Санкт-Петербург 2022 Содержание Введение Основные понятия Понятие числовой функции Аргумент функции Область определения функции Область значений функций Способы задания функций Аналитический Табличный Графический Классификация функций Чётность Периодичность Промежутки монотонности Ограниченность Точные верхние и нижние грани Наибольшее и наименьшее значение функции Суперпозиция Обратная функция Элементарные функции Введение Основные понятия Множества – совокупность объектов произвольной природы, каждый из которых называется элементом множества. Переменной называется величина, принимающая множество различных значений. Множества обозначаются заглавными буквами A, B, C и т.д. Переменные – буквами латинского алфавита a, b, c и т.д. Понятие числовой функции Пусть x, y – переменные x∈X, y∈Y, тогда: Переменная yназываетсяфункцией f(x) от переменнойx в области её изменения X, если по некоторому правилу или закону каждому значению x соответствует только одно значение y (из Y). Независимая переменная x называется аргументом функции. Областью определения функции называется множество значений x∈X, для которых функция определена. Областью значений функции называется множество Y всех значений y, которые функция принимает на области определения Способы задания функций Аналитический Аналитический способ задания функции – это правило или закон соответствия между значениями переменных, выражающий функциональную зависимость при помощи формулы, представляющей функцию в виде аналитического выражения, указывающего на действия над значением x, чтобы получить соответствующее значение y. Пример: f(x)=2x²+4x+6 Табличный В табличном способе задания функции соответствие между x и y задаётся при помощи таблицы. Пример: Таблица зависимости относительной влажности от температуры В 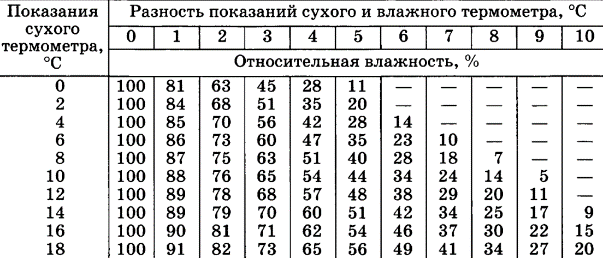 приведённой таблице аргументом функции можно считать показания термометра, а самой функцией относительную влажность. приведённой таблице аргументом функции можно считать показания термометра, а самой функцией относительную влажность.Графический В графическом способе задания функции используется график в координатах Oxy, где абсциссой точки является значение x, а ординатой значение y. График функции – множество точек плоскости с координатами (x, y). Для определения значения функции нужно спроецировать координату x на график, а полученную точку на графике спроецировать на ось Oy. 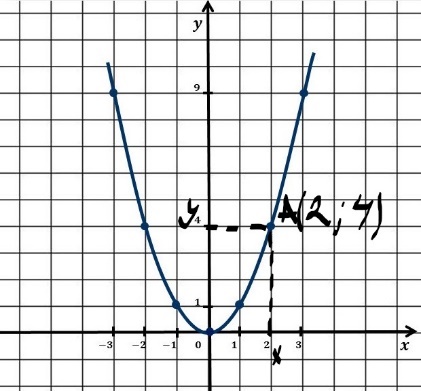 Классификация функций Чётность и нечётность Чётной функцией называется функция значение, которой не меняется при изменении знака переменной. 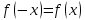 (1) (1)Нечётной функцией называется функция значение, которой меняется при изменении знака аргумента на противоположное. 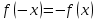 (2) (2)Ни чётной, ни нечётной функцией (или же функцией общего вида) называется функция, не являющаяся чётной или нечётной. Для определения чётности или нечётности функции нужно проверить условия (1) и (2), если ни одно из них не выполняется, то функция является функцией общего вида. Периодичность Периодическая функция – функция, повторяющая своё значение с некоторым интервалом аргумента, то есть не меняющая своего значения, при добавлении к аргументу периода 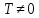 , на всей области её определения. , на всей области её определения.То есть выполняется условие 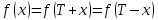 Исходя из этого определения 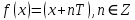 Функции, не имеющие периода – называются апериодическими. Стоит отметить, что все тригонометрические функции являются периодическими. Промежутки монотонности Промежутками монотонности функции называются интервалы, на которых функция возрастает или убывает. Возрастающая функция – функция, в которой большему значению аргумента соответствует большее значение функции. 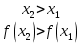 Убывающая функция – функция, в которой большему значению аргумента соответствует меньшее значение функции. 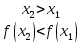 Если функция только убывает или только возрастает на заданном промежутке, то она называется монотонной. Ограниченность Функция называется ограниченной, если её область значений ограничена, т.е. все её значения лежат на ограниченном промежутке, в обратном случае функцию можно назвать неограниченной. Можно дать следующее определение ограниченности функции: функция у = f(x) называется ограниченной на всей области определения D(f), если существует такое число С>0, что |f(x)|≤C для каждой точки x∈D(f). Функция, ограниченная на некотором множестве X⊂D(f), может быть неограниченной на всей области определения. Например, функция у = 1/х ограничена при х є [1/10;10], но на всей области определения она является неограниченной. Точные верхние и нижние грани Функция 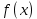 называется ограниченной сверху (снизу), если называется ограниченной сверху (снизу), если существует такое число A, что для всех 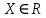 выполняется неравенство выполняется неравенство 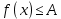 , ( , (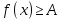 ). ). Точной верхней гранью 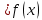 , ограниченной сверху функции называют наименьшее число, ограничивающее область значений функции. , ограниченной сверху функции называют наименьшее число, ограничивающее область значений функции.Т.е. это такое число а, для которого: 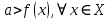 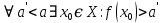 ъ ъВерхней гранью неограниченной сверху функции является 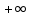 Точной нижней гранью 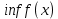 , ограниченной снизу функции называют наибольшее число, ограничивающее область значений функции. , ограниченной снизу функции называют наибольшее число, ограничивающее область значений функции.Т.е. это такое число b, для которого: 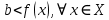 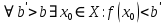 Нижней гранью неограниченной снизу функции является 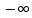 Наибольшее и наименьшее значение функции Наибольшее значение функции 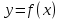 на некотором промежутке – это значение, которое при любом значении на некотором промежутке – это значение, которое при любом значении 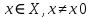 делает справедливым неравенство делает справедливым неравенство 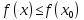 Наименьшее значение функции 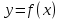 на некотором промежутке – это значение, которое при любом значении на некотором промежутке – это значение, которое при любом значении 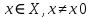 делает справедливым неравенство делает справедливым неравенство 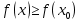 Суперпозиция функций Суперпозиция функций— это функция, полученная из некоторого множества функций путем подстановки одной функции в другую или отождествления переменных\ Множество всех возможных не эквивалентных друг другу суперпозиций данного множества функций образует замыкание данного множества функций. 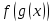 , где , где 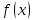 и и 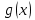 – некоторые функции – некоторые функцииСложная функция обозначается как  Обратная функция Пусть функция 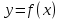 имеющая область определения X и множество значений Y. И пусть она обладает свойством: имеющая область определения X и множество значений Y. И пусть она обладает свойством: 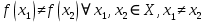 . .Тогда для любого 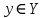 в соответствии можно сопоставить только один элемент в соответствии можно сопоставить только один элемент 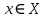 , для которого , для которого 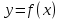 . Такое соответствие определяет функцию, которая называется обратной функцией. Обратная функция обозначается как . Такое соответствие определяет функцию, которая называется обратной функцией. Обратная функция обозначается как 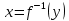 Элементарные функции Функции вида 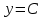 Данная функция называется постоянной, т.е. каждому значению аргумента икс соответствует одно и тоже значение функции равное C. Графиком данной функции является прямая параллельная оси абсцисс. Свойства: 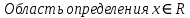 Область значений 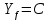 Ни чётная, ни нечётная Не имеет периода Функция монотонна на всей области определения Ограничена сверху и снизу Н 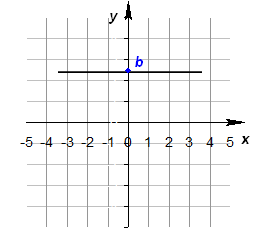 ет обратной функции ет обратной функцииФункции вида 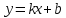 Свойства: Область определения функции - множество всех действительных чисел Множеством значений функции является множество всех действительных чисел Функция не имеет ни наибольшего, ни наименьшего значений Функция не является ни четной, ни нечетной (кроме особых случаев) Функция непериодическая Функция монотонно возрастает на области определения при k>0, монотонно убывает при k<0 Не ограничена ни сверху ни снизу Коэффициент k характеризует угол, который образует прямая с положительным направлением Ох. k называют угловым коэффициентом. Если k>0, то этот угол острый, если k<0 - тупой, если k=0, то прямая совпадает с осью Ох. При K>0 функция принимает отрицательные значения на промежутке 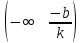 , положительные , положительные 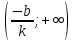 При K<0 функция принимает положительные значения на промежутке 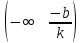 , отрицательные , отрицательные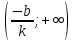 Обратная функция: 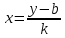 Графики: 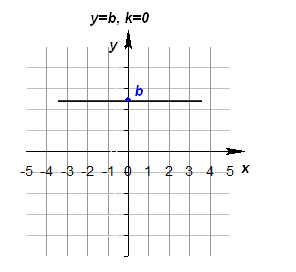 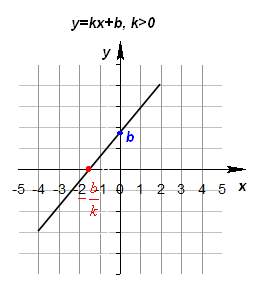 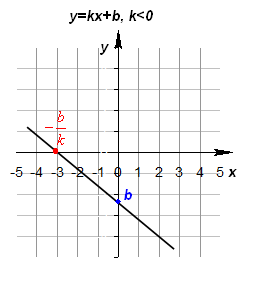 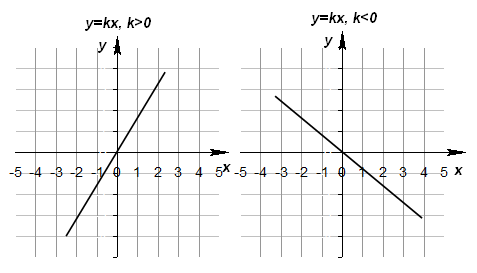 Функции вида 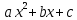 Парабола имеет вершину, ось, проведенная через вершину и параллельная оси Оу, делит параболу на две симметричные части. Вершиной параболы называется точка 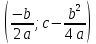 Свойства: Областью определения функции является множество всех действительных чисел. Множеством значений функции является промежуток 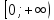 Значение функции в точке вершины является наименьшим, а наибольшего значения функция не имеет. Если b=0, то функция чётная, если b!=0, то ни чётная ни нечётная Не является периодической При а>0 ограничена снизу, при a<0 ограничена сверху Не является монотонной функцией на всей области определения. При а>0 убывает на промежутке 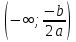 , возрастает , возрастает 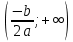 , при а<0 возрастает на промежутке , при а<0 возрастает на промежутке 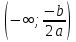 , убывает , убывает 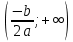 Графики 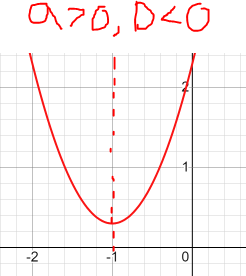 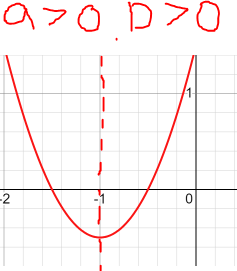 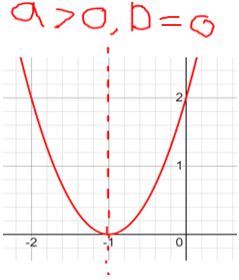 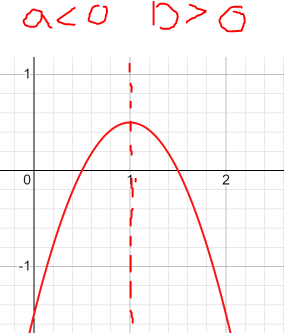 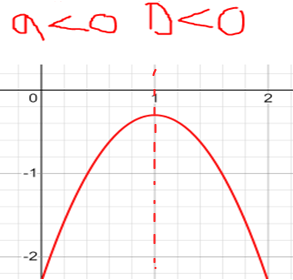 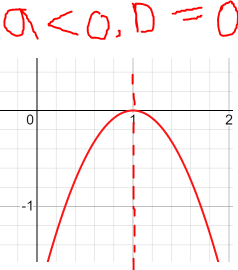 Функция вида 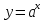 Функция, заданная формулой y=ax (где a>0,a≠1), называется показательной функцией с основанием a. Свойства: Область определения — множество R действительных чисел. Область значений — множество R всех положительных действительных чисел начиная от 0 его не включая При a>1 функция возрастает на всей числовой прямой; при 0 Ни чётная ни нечётная Не имеет ни наибольшего ни наименьшего значения Ограничена снизу, не ограничена сверху Не является периодической 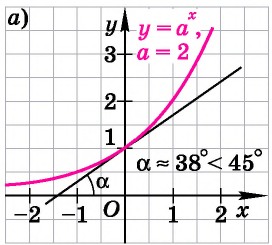 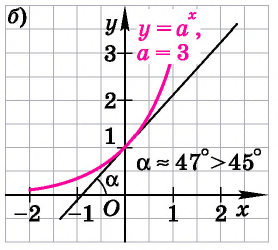 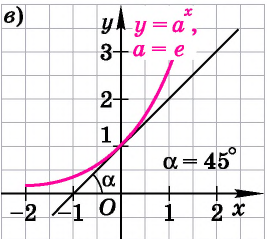 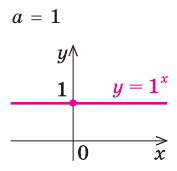 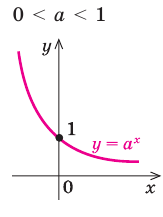 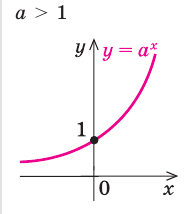 Функция вида 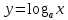 Свойства: Областью определения функции является множество всех действительных положительных чисел Областью значений является множество всех действительных чисел . Не имеет ни наибольшего ни наименьшего значений Ни чётна ни нечётна При а>0 монотонно возрастает, при а<0 монотонно убывает Не является периодической 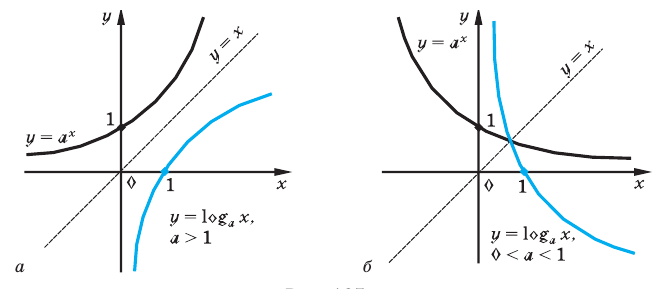 Показательная функция П Свойства: Область определения все действительные числа Область значений все действительные числа от нуля его не включая Ни чётная ни нечётная При а>1, возрастает на всей области определения, при а<1 убывает y>0 при всех значениях аргумента не ограничена не имеет ни наибольшего ни наименьшего значений 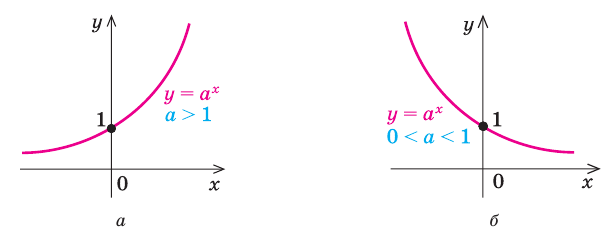 не является периодической не является периодическойТригонометрические функции Зависимость, при которой каждому действительному числу Свойства: Областью определения функции Множеством значений функции Периодичность функции Функция нечётная Наибольшее значение 1 Наименьшее -1 Ограничена сверху и снизу 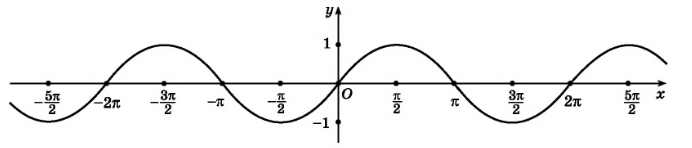 Функция косинуса Свойства: Область определения все действительные числа Область значений [-1;1] Период Т=2п Чётная Ограниченасверху и снизу Наибольшее значение 1 Наименьшее -1 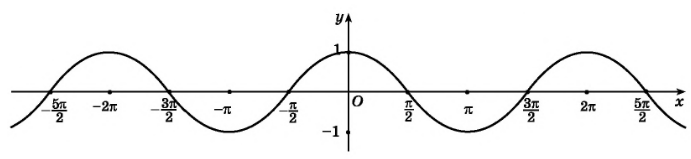 Функция тангенса котангенса З Зависимость, при которой каждому действительному числу Свойства тангенса: 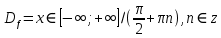 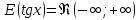 Наименьший период Т=2п Нечётная функция Не имеет ни наибольшего ни наименьшего значений Возрастает 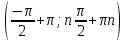  Свойства котангенса   Наименьший период Т=п Нечётная фнукция Убывает на  Не имеет ни наибольшего ни наименьшего значений 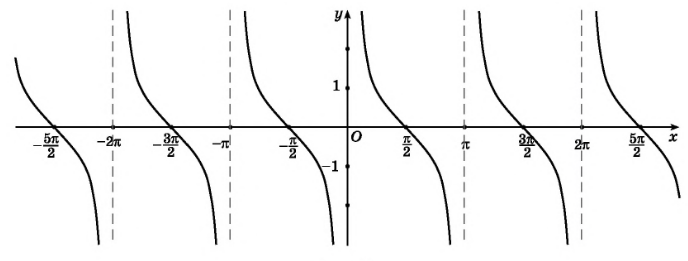 Обратные тригонометрические функции Арксинусом числа а называется число Арккосинусом числа а называется число Арктангенсом числа а называется число Арккотангенсом числа а называется число Свойства функции 1. Область определения 2. Область значений 3. 4 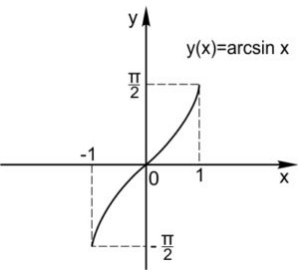 . Функция . Функция 5 6.обратаня функции Свойства функции 1. Область определения 2. Область значений 3. 4.Эта функция общего вида — она не является ни четной, ни нечетной. 5 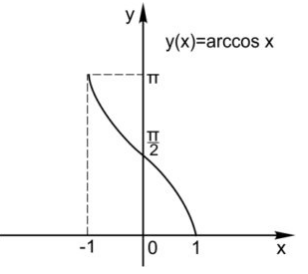 . Функция является строго убывающей. Наибольшее значение, равное . Функция является строго убывающей. Наибольшее значение, равное 6. Функции Свойства функции 1. Область определения 2. Область значений 3. Функция 4. Функция 5 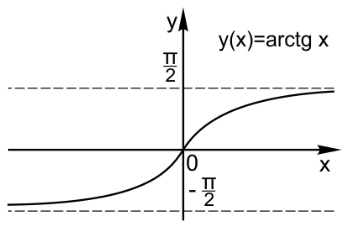 . Прямые . Прямые 6. Функции Свойства функции 1. Область определения 2. Область значений 3. Функция 4. Функция 5. Прямые 6 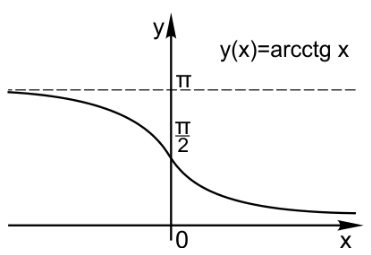 . Функции . Функции Функции 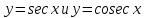 Пусть х – произвольный угол или число. Величина, обратная косинусу этого угла (числа) – называется секансом х и обозначается через sec x. Таким образом, функция секанс (y = sec x) определяется формулой: 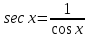 Свойства Область определения секанса: x∈(-∞;π/2+ πn)∪(π/2+ πn, +∞), n∈Z Область значений секанса: y∈(-∞;-1]∪ [1, +∞) Секанс – периодическая функция (период секанса равен 2π) Секанс – четная функция, так как косинус – четная функция Убывает на 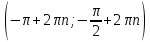 и и 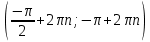 Возрастает на 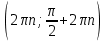 и и 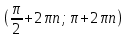 |