олимпиадные задания 4 класс. Математика и русский олимпиада. Решение (1 способ)
 Скачать 28.51 Kb. Скачать 28.51 Kb.
|
|
Математика В ПОИСКАХ ЧИСЛА На какое наименьшее натуральное число нужно умножить 126 984, чтобы получилось число, которое записывается одними восьмёрками? Решение (1 способ): Чтобы найти наименьшее число, воспользуемся методом полного перебора. Будем умножать на все числа в порядке возрастания, начиная с единицы: 126 984 1 = . . . . . 4 4 ≠ 8 ⇒ 1 не подходит (даже последняя цифра произведения – не восьмёрка); 126 984 2 = . . . . 68 6 ≠ 8 ⇒ 2 не подходит; 126 984 3 = . . . . . 2 2 ≠ 8 ⇒ 3 не подходит; 126 984 4 = . . . . . 6 6 ≠ 8 ⇒ 4 не подходит; 126 984 5 = . . . . . 0 0 ≠ 8 ⇒ 5 не подходит; 126 984 6 = . . . . . 4 4 ≠ 8 ⇒ 6 не подходит; 126 984 7 = 888 888 произведение записано восьмёрками ⇒ 7 подходит. № 4.4. ХУДОЖНИКИ Ася, Маша и Галя нарисовали круг, квадрат и треугольник (каждая девочка нарисовала только одну фигуру). Ася сказала, что Галя нарисовала круг. Маша сказала, что Ася нарисовала квадрат. Галя сказала: «Я нарисовала квадрат». Кто что нарисовал, если только одна из девочек солгала? Решение (способ 1): Предположим, что солгала Ася, тогда Галя и Маша сказали правду. По их высказываниям, Галя и Ася нарисовали квадрат. Но двое не могли нарисовать одну фигуру. Значит, Ася не солгала, а сказала правду. Предположим, что солгала Маша, тогда Галя и Ася сказали правду. По их высказываниям, Галя нарисовала и круг, и квадрат. Но Галя не могла нарисовать две разные фигуры. Значит, Маша не солгала, а сказала правду. Формулировка задания («кто что нарисовал…») подразумевает, что будут найдены все варианты и доказано, что других быть не может. Именно поэтому требуется словесное решение и недостаточно изобразить только таблицу, в которой плюсами и минусами указано, какую фигуру могла и не могла нарисовать каждая девочка. Доказательство можно провести с использованием метода (полного) перебора. Если Ася и Маша не солгали, значит, солгала Галя. Узнаем тогда, кто какую фигуру нарисовал. Из слов Аси, которая сказала правду, можно узнать, что Галя нарисовала круг, а из слов Маши – что Ася нарисовала квадрат. Оставшуюся фигуру – треугольник – нарисовала Маша. 1. Разминка: а) В двух залах 50 стульев. Когда из одного зала вынесли 10 стульев, то в залах осталось стульев поровну. Сколько стульев было в каждом зале первоначально? б) Найти сумму 1+2+3+4+…+98+99+100. в) Что больше половина половины 20 или четверть четверти 80? г) К трёхзначному числу слева приписали цифру 1. На сколько увеличилось число? д) Масса ящика с лимонами 25 кг. После продажи половины всех лимонов, ящик поставили на весы. Весы показали 15 кг. Найдите массу пустого ящика. е) 3 курицы за 3 дня снесли 3 яйца. Сколько яиц снесут 6 куриц за 6 дней? 9 куриц за 9 дней? ж) Длина забора 20 метров. Сколько в заборе столбов, если столб от столба стоит на расстоянии двух метров? 2. Нескольким обезьянам раздали 50 бананов так, чтобы каждая получила хотя бы по 1 банану и ни у каких двух обезьян не было поровну . Какое наибольшее количество обезьян могли получить бананы? 3. Запиши ответ цифрами и словами: а) назови 2 числа, у которых количество цифр равно количеству букв, составляющих название каждого из этих чисел. б) назови 2 числа, у которых количество букв, составляющих название каждого из этих чисел равно самому числу. 4. Прямоугольный лист бумаги со сторонами 8 см 4 см разрезали на 4 равных части, а затем из них составили квадрат. Как это сделали? Выполни рисунок. 5. В банку попал 1 микроб, и через 10 минут банка была наполнена микробами, причём известно, что количество микробов ежеминутно удваивалось. За сколько минут банка была наполнена микробами наполовину? Запиши ответ и свои рассуждения. 6. Два велосипедиста едут навстречу друг другу, расстояние между ними 240 км. В начальный момент движения взлетает муха и принимается летать вперёд и назад между велосипедистами, пока те не встретятся. Велосипедисты всё это ехали со скоростью 40 км/ч, а муха летала со скоростью 60 км/ч. Какое расстояние пролетела муха? 7. Представь, что ты с другом путешествуешь на суперпоезде. Вы едете в соседних вагонах. Друг едет в 17 вагоне с начала поезда, а ты в 134 с конца. Сколько вагонов в поезде? Запиши ответ и свои рассуждения. 8. Старые часы отстают на 20 секунд в час. Сколько времени они покажут через сутки после того, как стрелки установили на 12 часов? Запиши решение по действиям и свои рассуждения. 9. Маленький коала съедает листья с одного эвкалиптового дерева за 10 часов, а каждый из его родителей ест вдвое быстрее. За сколько времени это семейство объест все листья с одного эвкалиптового дерева? Запиши решение по действиям с пояснениями и ответ. Ответы: 1. Разминка: а) В 1 зале – 30 стульев, во 2 зале – 20 стульев. б) 5050 в) равно г) на 1000 д) 5 кг е) 1 курица за 3 дня снесёт 1 яйцо, значит за 6 дней она снесёт 2 яйца, за 9 дней – 3 яйца, тогда 6 куриц за 6 дней снесут 12 яиц, а 9 куриц – 27 яиц. ж) если 1 считается, то 11 столбов, если не считается, то 10 столбов. 2. 9 обезьян 3. а) 100 – сто, 1000000 – миллион; б) три, одиннадцать 4. 5. 1 мин. – 2, 2 мин. – 4, 3 мин. – 8, 4 мин. – 16, 5 мин. – 32, 6 мин. – 64, 7 мин. – 128, 8 мин. – 256, 9 мин. – 512, 10 мин. – 1024. 1024: 2=512 – 9 мин. 6. 40х2=80 (км\ч) – скорость сближения 240:80=3 (ч.) – были в пути 60х3=180(км) 7. 251 вагон 8. 1) 24х20=480(сек) – отстали 2) 480:60=8(мин) – отстали 3) 24х60=1440(мин) – в сутках. 4) 1440 – 8= 1432 (мин) = 11ч 52 мин – стали показывать. 9. Допустим, что на дереве 1000 листьев. 1) 1000:10=100(л.) – съедает за 1 час маленький коала. 2) 100х2=200(л.) – съедает за 1 час 1 родитель. 3) 200х2+100=500(л.) – съедает за 1 час вся семья. 4) 1000:500=2(ч.) – за это время семейство объест все листья с 1 дерева 2. Одни часы отстают на 25 минут, показывая 1 ч 50 мин. Какое время показывают другие часы, если они забегают на 15 мин? (2балла)_________ 3.Чему равны стороны прямоугольника, площадь которого равна 12 см, а периметр равен 26 см? (1 балл)__________________________________. 4. Сколько получится, если сложить наибольшее нечетное двузначное число и наименьшее четное трехзначное число? (1 балл) __________________________. 5. В каждой цепочке чисел найди закономерность и вставь пропущенные числа (1 цепочка – 1 балл): 1) 3, 6, __, 12, 15, 18. 2) 1, 8, 11, 18, ___, 28, 31. 3) 2, 2, 4, 4, ___, 6, 8, 8. 4) 24, 21, ___, 15, 12. 5) 65, 60, 55, ____, 45, 40, 35. 6. Напишите наименьшее четырехзначное число, в котором все цифры различные. (1 балл)____________________________. 7. Три подружки - Вера, Оля и Таня пошли в лес по ягоды. Для сбора ягод у них были корзина, лукошко и ведерко. Известно, что Оля была не с корзиной и не с лукошком, Вера - не с лукошком. Что с собой взяла каждая девочка для сбора ягод? (3 балла) Вера - ______________, Таня -__________, Оля - _______________. 8. Мотоциклист за три дня проехал 980 км. За первые два дня он проехал 725 км, при этом он во второй день проехал на 123 км больше, чем в третий день. Сколько километров он проехал в каждый из этих трех дней? (4 балла) I день _______, II день _______, III день ________. 9. Напишите цифрами число, состоящее из 22 миллионов 22 тысяч 22 сотен и 22 единиц. (2 балла)________________________________. 10. В туристический лагерь прибыло 240 учеников из г. Москвы и Орла. Мальчиков среди прибывших было 125 человек, из которых 65 - москвичи. В числе учеников, прибывших из Орла, девочек было 53. Сколько всего учеников прибыло из Москвы? (4 балла)_____________. 4 класс: 2. 1 час 50 мин+25 мин= 2 часа15 мин (2 балла) 2 часа 15 мин+15 мин=2 часа 30мин 3. Стороны прямоугольника 12 см и 1 см. (1 балл) 4.199 (1 балл) 5. 1) 9; 2)21; 3)6; 4)18; 5) 50; (1 цепочка - 1 балл) 6. 1023 (1 балл) 7. Вера была с корзинкой, Оля - с ведерком, Таня -с лукошком. ( 3 балла) 8. ( 4 балла) 1) 980 - 725 = 255 (км) - проехал в третий день; 2) 255 + 123 = 378 (км) - проехал во второй день; 3) 725 - 378 = 347 (км) - проехал в первый день. Ответ: в первый день мотоциклист проехал 347 км, во второй - 378, в третий - 255 км. 9. 22 024 222 ( 2 балла) 10. ( 4 балла) 1) 240-125=115 девочек из Москвы и Орла 2) 115-53=62 девочек из Москвы 3) 65+62=127 детей из Москвы 1 Задача 4.2 Петя взял из коробки половину конфет и засунул их в два кармана. Решив, что взял слишком много, Петя достал по 6 конфет из каждого кармана и положил обратно в коробку. На сколько в коробке стало больше конфет, чем в карманах у Пети? Ответ: 24. Решение. Пусть x конфет лежало в одном кармане Пети до того, как он вернул часть конфет обратно в коробку. В коробке в этот момент было 2x конфет. После того, как Петя из каждого кармана достал по 6 конфет, у него осталось (x − 6) + (x − 6) = 2x − 12 конфет, а в коробке стало 2x + 12 конфет. Таким образом, в коробке стало на (2x + 12) −(2x − 12) = 24 конфеты больше, чем у Пети. Задача 4.3 Денис вырезал из клетчатого квадратного листа бумаги корабль (см. рисунок). Из какого наименьшего количество клеточек мог состоять квадратный лист бумаги до вырезания из него корабля? 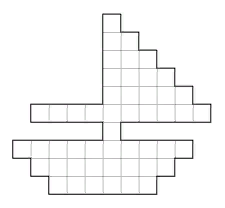 Ответ: 121 Решение. На рисунке ниже видно, что корабль можно вырезать из прямоугольника 10 × 11. Но по условию задачи корабль вырезали из квадратного листа бумаги. Получается, что минимальный квадрат, из которого могли вырезать такой корабль, — это квадрат 11×11. Он состоит из 121 клеточки. Задача 4.5 На лугу паслось 12 коров. Пастухи пригнали стадо овец. Овец оказалось больше, чем у коров ушей, но меньше, чем у коров ног. Сколько было овец, если их в 12 раз больше, чем пастухов? Ответ: 36 овец. Решение. Так как овец в 12 раз больше, чем пастухов, то количество овец делится на 12. Кроме этого, овец больше, чем 12⋅2 = 24 (количество ушей у коров) и меньше, чем 12⋅4 = 48 (количество ног у коров). Единственное число, делящееся на 12 и находящееся между 24 и 48, — это 36. Задача 4.6 За тремя двухместными партами, стоящими друг за другом, сидят Артём, Боря, Вова, Гриша, Дима и Женя. Других учеников в классе нет. Известно, что: Дима постоянно отвлекает сидящего перед ним ученика; Боря смотрит в затылок Жене; Артём и Гриша — близкие друзья и сидят за одной партой; учитель запретил Вове и Жене сидеть за одной партой. Кто сидит за второй партой? Ответ: Женя и Дима. Решение. Посмотрим, кто может сидеть с Женей за одной партой. Артём и Гриша сидят вместе, значит, никто из них не может сидеть с Женей за одной партой. По условию задачи Боря сидит за Женей, то есть не за одной партой с ним. Вове запрещено сидеть рядом с Женей. Получается, что единственный, кто может сидеть рядом с Женей — это Дима. Но Дима не может сидеть за первой партой, так как перед ним сидит ученик, которого он отвлекает; а Женя не может сидеть за последней, так как сзади него сидит Боря. Таким образом, Женя и Дима сидят за второй партой. Русский язык Задание № 1 (5 баллов) Составьте на основе данных словосочетаний сложные слова-существительные и запишите их: хранить овощи, косить сено, снимать фото, зоологический сад, электрический счётчик. Учтите, что каждое сложное слово, составленное Вами правильно, пишется слитно. Модель ответа и критерии оценивания Овощехранилище, сенокос (допустимо: сенокосилка – 0,5 балла), фотосъёмка, зоосад, электросчётчик. За каждое слово – 1 балл. За каждую орфографическую ошибку снимается 1 балл. Отрицательный балл не ставится. Итого 5 баллов. Задание № 5 (6 баллов) Даны русские слова и их переводы на белорусский язык: смеяться – смяяцца, снять – зняць, сварить – зварыць. Какая буква будет первой в белорусских переводах русских слов: соль – (бел.) ___оль, слушать – (бел.) __лухаць, свалить – (бел.) __валіць, сбежать – (бел.) __бегчы, смягчить – (бел.) __ мякчыць? Объясните Ваше решение. Модель ответа и критерии оценивания Соль – соль, слушать – слухаць, свалить – зваліць, сбежать – збегчы, смягчить – змякчыць. За каждый пример – 1 балл. Буква с не меняется на з в корне слова. – 1 балл. Допустимо: русской с в приставке соответствует белорусская з. Итого 6 баллов. Задание № 9 (7 баллов) Распределите глаголы по группам в зависимости от слова (укажите часть речи), от которого оно образовано: зеленеет, пестреет, беседует, вечереет, бороздит. Модель ответа и критерии От имени существительного (1 балл): беседует, бороздит, вечереет. От имени прилагательного (1 балл): зеленеет, пестреет. За каждый глагол – 1 балл. Всего 7 баллов. Задание № 10 (12 баллов) Восстановите искажённые фразеологизмы в их первоначальном виде: спустя манжеты, он в математике кошку съел, делать из букашки слона, ходить уткой, бежал сломя нос, сапоги супа просят. Модель ответа и критерии Восстановленный фразеологизм спустя манжеты- спустя рукава он в математике кошку съел- собаку съел делать из букашки слона- делать из мухи слона ходить уткой- ходить гоголем бежал сломя нос- бежал сломя голову сапоги супа просят -сапоги каши просят По 2 балла за каждый правильный ответ. Всего 12 баллов. |
