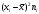высшая математика. Решение а Событие а номер наудачу выбранного билета четный
 Скачать 294.29 Kb. Скачать 294.29 Kb.
|
|
Вариант 1 Задание 1 В урне тысяча лотерейных билетов с номерами от 1 до 1000. Найти вероятность того, что номер наудачу вынутого билета: а) четный; б) нечетный; в) делится на 3; г) не делится на 4. Решение а) Событие А – номер наудачу выбранного билета – четный. Найдем вероятность данного события по классическому определению вероятности. Тогда вероятность события А равна  , где m – число элементарных событий, входящих в А (или число исходов, благоприятствующих появлению события А). , где m – число элементарных событий, входящих в А (или число исходов, благоприятствующих появлению события А). Число n – общее количество билетов. В данном случае n = 1000 Количество четных билетов: m = 500. Тогда искомая вероятность: 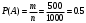 б) Событие В – номер наудачу выбранного билета – четный. События А и В составляют полную группу. Поэтому: Р(В) = 1 – Р(А) = 1 – 0.5 = 0.5 в) Событие С – номер наудачу выбранного билета делится на 3. Решаем аналогично пункту А. В данном случае n = 1000 m = 333. Отсюда искомая вероятность: 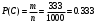 г) Событие D – номер наудачу выбранного билета не делится на 4. Найдем вероятность противоположного события. Событие D1 – номер наудачу выбранного билета делится на 4. В данном случае n = 1000 m = 250. Отсюда вероятность события D1: 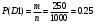 События D и D1 составляют полную группу. Поэтому: Р(D) = 1 – Р(D) = 1 – 0.25 = 0.75 Ответ: а) Р(А) = 0.5 б) Р(В) = 0.5 в) Р(С) = 0.333 г) P(D) = 0.75 Задание 2 Три фирмы выполняют один и тот же заказ. Вероятность того, что первая фирма выполнит заказ в срок 0.75, вторая — 0.8, третья — 0.9, по отдельности. Определить вероятность того, что: а) одновременно первая и вторая выполнят заказ, а третья не успеет; 6) все три одновременно не выполнят заказ в срок. Решение Обозначим событие Аi – i-ая фирма выполнила заказ в срок, событие 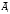 – i-ая фирма не выполнила заказ в срок. – i-ая фирма не выполнила заказ в срок.а) Пусть событие В – одновременно первая и вторая выполнят заказ, а третья не успеет. Событие В произойдет, если одновременно произойдут все из независимых событий: В1 – первая фирма выполнит заказ. В2 – вторая фирма выполнит заказ. В3 – третья фирма не выполнит заказ. Найдем вероятность события В по формуле умножения вероятностей независимых событий: 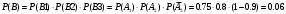 б) Пусть событие С – все три фирмы одновременно не выполнят заказ в срок. Событие С произойдет, если одновременно произойдут все из независимых событий: С1 – первая фирма не выполнит заказ. С2 – вторая фирма не выполнит заказ. С3 – третья фирма не выполнит заказ. Найдем вероятность события С по формуле умножения вероятностей независимых событий: 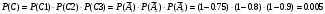 Ответ: а) Р(В) = 0.06 б) Р(С) = 0.005 Задание 3 В клетке 30 попугаев: 20 говорящих и 10 не говорящих. Наудачу выбирают 4 попугая. Какова вероятность того, что среди них трое будут говорящих? Решение Пусть событие А – из 4 наудачу выбранных попугаев трое будут говорящих. Найдем вероятность данного события по классическому определению вероятности. Тогда вероятность события А равна  , где m – число элементарных событий, входящих в А (или число исходов, благоприятствующих появлению события А). , где m – число элементарных событий, входящих в А (или число исходов, благоприятствующих появлению события А). Число n – количество способов выбрать 4 попугая из 30 без учета порядка. В данном случае 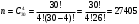 Чтобы произошло событие А необходимо выбрать 3 говорящих попугая из имеющихся 20 и 1 неговорящего из имеющихся 10.  Тогда искомая вероятность: 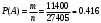 Ответ: Р(А) = 0.416 Задание 4 На экспертизу под скрытыми девизами поступают проекты от трех конкурирующих фирм. Вероятность того что проект первой фирмы пройдет экспертизу с положительной оценкой равна 0.8, второй — 0.6, третий — 0.9. Для экспертизы выбрали наудачу только один проект. Он ее прошел с хорошей оценкой. Какова вероятность того, что это был проект первой фирмы? Решение Пусть событие А – проект пройдет экспертизу с положительной оценкой. Введём три гипотезы: Н1 – проект от первой фирмы,  ; ;Н2 – проект от второй фирмы,  ; ;Н3 – проект от третьей фирмы,  ; ;Тогда условные вероятности события А по условию: 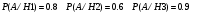 Если событие А уже произошло, то условную вероятность P(H1/A) найдем по формуле Байеса:  Ответ: а) Р(Н1/А) = 0.3478 Задание 5 Производится ряд выстрелов по мишени с вероятностью попадания 0.7 при каждом выстреле; стрельба ведется до первого попадания в мишень, но не свыше 5 выстрелов. Найти закон распределения, математическое ожидание и дисперсию числа произведенных выстрелов. Построить функцию распределения, определить вероятность того, что число выстрелов до первого попадания будет не меньше трех. Решение Пусть случайная величина Х – число произведенных выстрелов. При данных условиях случайная величина Х может принимать значения от 1 до 5. Найдем соответствующие вероятности.  Запишем закон распределения в виде таблицы:
Математическое ожидание: 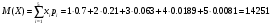 Найдем дисперсию: 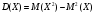 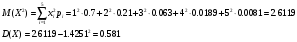 Составим функцию распределения. По определению 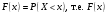 есть вероятность того, что случайная величина X примет значение меньше, чем x. есть вероятность того, что случайная величина X примет значение меньше, чем x. 1. При х ≤ 1 F(x) = P(X < 0) = 0 2. При 1 < х ≤ 2 F(x) = P(X < 2) = P(X = 1) = 0.7 3. При 2 < х ≤ 3 F(x) = P(X < 3) = P(X = 1) + Р(Х = 2) = 0.91 4. При 3 < х ≤ 4 F(x) = P(X < 4) = 0.973 5. При 4 < х ≤ 5 F(x) = P(X < 5) = 0.9919 6. При x > 5 F(x) = 1 Таким образом, функция распределения примет вид: 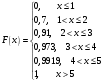 Вероятность того, что число выстрелов до первого попадания будет не меньше трех: Р(X ≥ 3) = P(X = 3) + P(X = 4) + P(X = 5) = 0.063 + 0.0189 + 0.0081 = 0.09 График функции распределения: 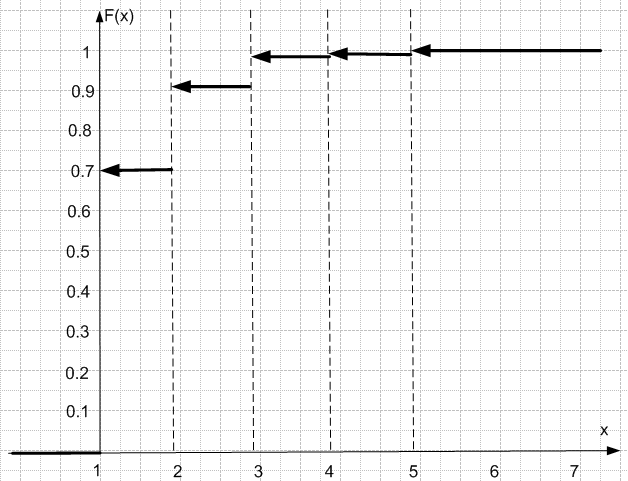 Ответ: M(X) = 1.4251 D(X) = 0.581 Р(X ≥ 3) = 0.09 Задание 6 Для непрерывной случайной величины задана плотность распределения 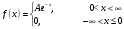 Требуется построить графики плотности распределения и функции распределения, определив предварительно параметр А. Найти математическое ожидание, дисперсию, среднеквадратическое отклонение. Найти вероятность того, что отклонение случайной величины от математического ожидания будет не более среднеквадратического отклонения. Решение Из условия нормировки:  Отсюда параметр А = 1 Найдем функцию распределения: На интервале 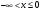 F(x) = 0 F(x) = 0На интервале 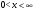  Функция распределения: 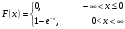 Графики: 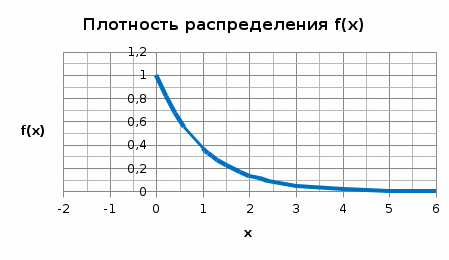 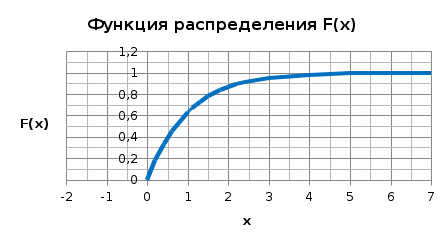 Найдем математическое ожидание: 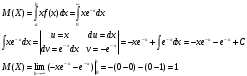 Чтобы найти дисперсию непрерывной случайной величины Х, найдём математическое ожидание случайной величины Х 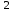 : :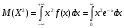 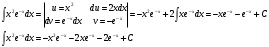 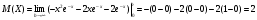 Дисперсию найдем по формуле: 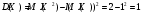 Среднее квадратическое отклонение:  Найдем вероятность того, что отклонение случайной величины от математического ожидания будет не более среднеквадратического отклонения. В данном случае это вероятность: Р(0 < x < 2). Lля вычисления вероятности попадания непрерывной случайной величины в интервал 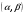 можно применить одну из формул: можно применить одну из формул: . .Применим вторую формулу:  Ответ: А = 1 М(Х) = 1 D(X) = 1 σ(X) = 1 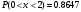 Задание 7 При обследовании 50 членов семей рабочих и служащих установлено следующее количество членов семьи: 5; 3; 2; 1; 4; 6; 3; 7; 9; 1; 3; 2; 5; 6; 8; 2; 5; 2; 3; 6; 8; 3; 4; 4; 5; 6; 5; 4; 7; 5; 6; 4; 8; 7; 4; 5; 7; 8; 6; 5; 7; 5; 6; 6; 7; 3; 4; 6; 5; 4. Составьте вариационный ряд распределения частот. Постройте полигон распределения частот, кумуляту. Определите среднее число членов семьи, среднеквадратическое отклонение. Решение Составим вариационный ряд, для чего каждой варианте поставим в соответствие ее частоту:
Строим полигон частот:  Составляем таблицу накопленных относительных частот:
Строим кумуляту:  Составим вспомогательную таблицу:
Находим среднее значение: 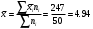 Дисперсия:  Среднее квадратическое отклонение: 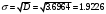 Ответ:  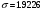 Задание 8 Автомат штампует детали. Контролируется длина детали X, которая распределена нормально с математическим ожиданием (проектная длина), равным 50 мм. Фактически длина изготовленных деталей не менее 32 и не более 68 мм. Найти вероятность того, что длина наудачу взятой детали: а) больше 55 мм; б) меньше 40 мм. Решение По условию математическое ожидание а = 50. Очевидно, что 50 – 32 = 68 – 50 = 18 Практически достоверным является тот факт, что нормально распределённая случайная величина Х примет значение из промежутка (а – 3σ, а + 3σ). Исходя из этого, 3σ = 18 и σ = 6 Вероятность того, что непрерывная случайная величина, распределенная по нормальному закону, примет значение на интервале 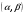 , равна , равна 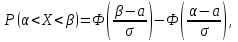 где Ф(x) – функция Лапласа. То есть, для пункта а интервал (55, +∞) Отсюда: 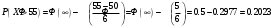 для пункта б интервал (-∞, 40) Отсюда:  Ответ: P(X > 55) = 0.2023 P(X < 40) = 0.0478 Задание 9 С помощью собственно - случайного повторного отбора фирма провела обследование 900 своих служащих. Среди обследованных оказалось 270 женщин. Определите с вероятностью 0.9 доверительный интервал, накрывающий неизвестную долю женщин во всѐм коллективе фирмы. Решение По условию задачи m = 270 n = 900 γ = 0.9 В данном случае выборочная доля: 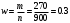 Предельная ошибка выборки в случае повторного отбора: 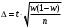 Значение t находим из таблицы функции Лапласа: 2Ф(t) = 0.9 t = 1.64 Отсюда:  Находим доверительный интервал для генеральной доли  Подставляем значения: 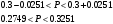 Ответ: доля женщин в коллективе фирмы с вероятностью 0.9 составляет от 0.2749 до 0.3251. |