Решение задач методом изоклин. МатематикаДСа. Решение Для получения уравнения изоклин примем, тогда Изоклинами являются гиперболы
 Скачать 149.91 Kb. Скачать 149.91 Kb.
|
|
1.Методом изоклин построить интегральные кривые уравнения 1.1 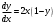 Решение: Для получения уравнения изоклин примем 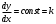 , тогда , тогда Изоклинами являются гиперболы. Изоклины симметричны относительно прямой  , т.е. интегральные кривые симметричны оси , т.е. интегральные кривые симметричны оси 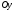 . .При 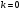 изоклина – прямая линия изоклина – прямая линия  Вдоль этой изоклины интегральная кривая имеет нулевой наклон, т.е. прямая  также является решением исходного уравнения. также является решением исходного уравнения.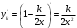 Т.о. наклон интегральных кривых определяется знаком 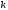 и из уравнения и из уравнения 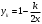 наклон интегральных кривых положительный во II и IV четвертях, отрицательный – в I и III. наклон интегральных кривых положительный во II и IV четвертях, отрицательный – в I и III.Для определения вогнутости найдем вторую производную из исходного уравнения:  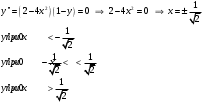 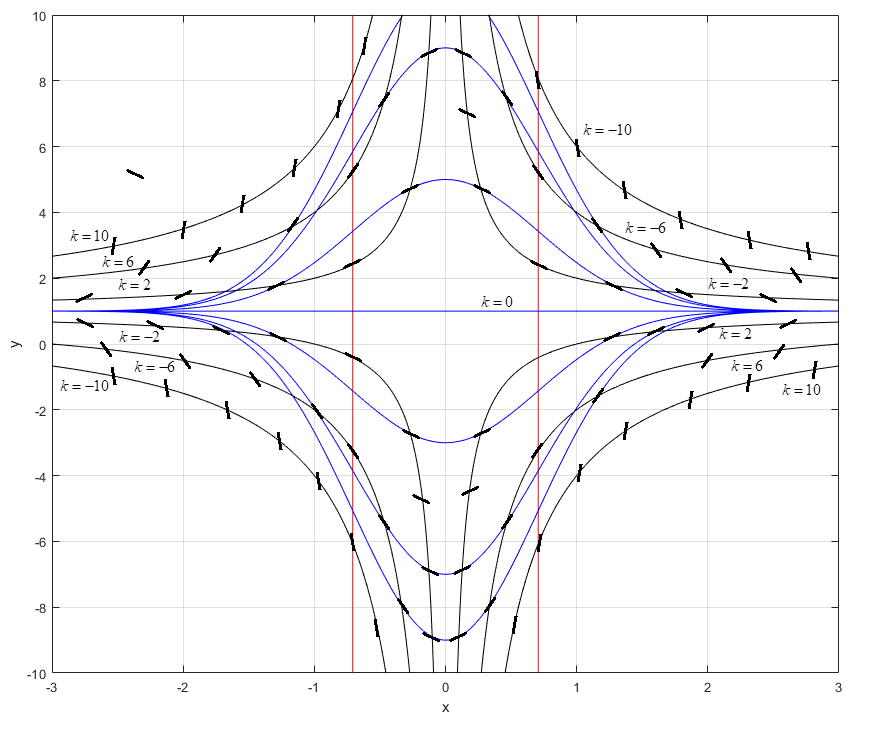 2.Решить уравнение, допускающее понижения порядка 2.1  Решение: Т.к. уравнение не содержит самой неизвестной функции, понизим порядок уравнения заменой  Подставим 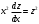 Полученное уравнение является уравнением с разделяющимися переменными  Проинтегрируем обе части 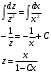 Произведем обратную замену  Проинтегрируем 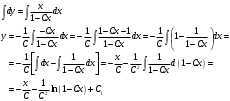 Полученное общее решение:  3.Решить систему уравнений 3.1 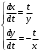 Решение: Выразив независимую переменную из каждого уравнения, получим 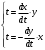 Отсюда 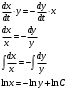 Потенцируя, получим 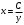 Отсюда  Перепишем первое уравнение исходной системы в виде:  Отсюда  Здесь в силу произвольности констант 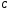 и и 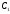 приняли: приняли: 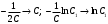 Чтобы найти решение 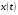 используем второе уравнение исходной системы: используем второе уравнение исходной системы: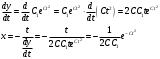 Общее решение системы: 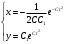 4.Вероятность появления события в каждом испытании равна 0,7. Сколько нужно провести испытаний, чтобы наивероятнейшее число появлений события равнялось 10? Решение: Наивероятнейшее число событий в схеме Бернулли (серия из  испытаний, в каждом из которых вероятность появления события одинакова и равна испытаний, в каждом из которых вероятность появления события одинакова и равна 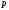 ) определяется из соотношения ) определяется из соотношения По формуле вероятности обратного события вероятность 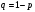 Из условия задачи 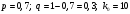 Подставим в неравенство:  Решим полученную систему неравенств: 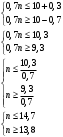 Т.к. число испытаний может принимать только целые значения, система имеет единственное решение:  Ответ:  |
