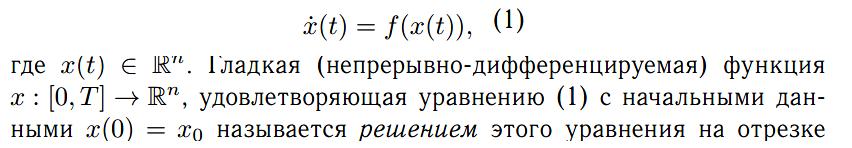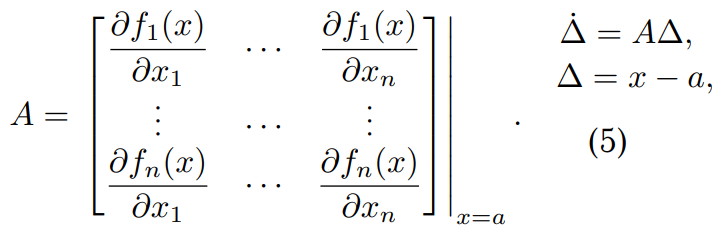Шпаргалка по Линейным системам. Лаба 1. Решение для промежутка 0, , т е. решается следующая задача Коши

Название	Решение для промежутка 0, , т е. решается следующая задача Коши
Анкор	Шпаргалка по Линейным системам
Дата	09.02.2023
Размер	1.78 Mb.
Формат файла
Имя файла	Лаба 1.docx
Тип	Решение #928058

Лаба 1 Линейные Системы

Неустойчивость по Ляпунову – это логическое отрицание устойчивости по Ляпунову. Тривиальное решение 𝑥(𝑡) ≡ 0 линейной системы (1) называется неустойчивым по Ляпунову, если существует такое 𝜀 > 0 и такие начальные данные, для которых выполнено: |𝑥(𝑡, 𝑥0)| > 𝜀.

характеристические многочлены линейной динамической системы c постоянными матричными коэффициентами.

	На самом деле все функциональные модели «вход-выход» неявно подразумевают модель в пространстве состояний, иначе негде было бы взять существование и единственность решения. Вход-выход к ФПС:
	Слайд 23 - про характериск-й многочлен и теорему. (ФПС-входвыход) Стр. 46 - передаточная функция

Лабораторная 4 Дискретные

Слайд 21 - дискретизация

Лабораторная 5 Задержка

Для поиска решения системы (1) можно использовать метод шагов, предложенный Р. Беллманом [59]. Его идея заключается в следующем. Вначале ищется решение для промежутка 𝑡 ∈ [0, ℎ], т.е. решается следующая задача Коши:

Затем процедура повторяется для интервалов времени [ℎ, 2ℎ], [2ℎ, 3ℎ] и т.д. Если 𝜙(𝑡) ≡ const, то решения уравнения (1) являются многочленами, явно зависящими от переменной 𝑡.

Разумихина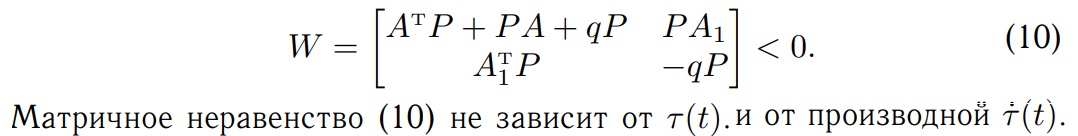

Данное матричное неравенство не является линейным, так как оно содержит член 𝑞𝑃, где 𝑞 и 𝑃 – неизвестные. Однако оно легко сводится к линейному путем выбора конкретного значения 𝑞 > 0. Таким образом, мы получили достаточные условия устойчивости тривиального решения 𝑥(𝑡) ≡ 0 для систем с произвольной задержкой (без ограничений). Задача свелась к проверки разрешимости системы матричных неравенств 𝑃 > 0 и (10).

Критерий сильвестора: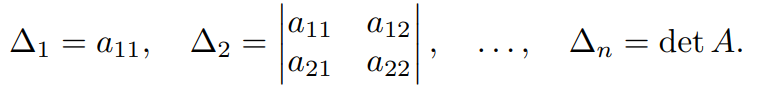

Критерий Сильвестра: Для положительной определенности матрицы 𝐴 необходимо и достаточно, чтобы все ее угловые миноры ∆𝑖 были положительны. Для отрицательной определённости матрицы 𝐴 необходимо и достаточно, чтобы ее угловые миноры четного порядка были положительны, а нечетного порядка – отрицательны.

Лабораторная 6 ДЕСКРИПТОРНЫЙ МЕТОД

Ранее мы рассматривали методы, гарантирующие устойчивость системы с запаздыванием при любом запаздывании. Интересно было бы рассмотреть метод, гарантирующий устойчивость системы с запаздыванием при задержке, принадлежащей некоторому промежутку. Одним из таких методов является дескрипторный метод [63, 64]. Будем рассматривать линейную систему с запаздыванием: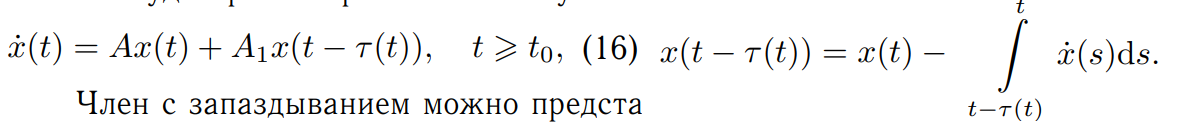

Полученная дескрипторная система эквивалентна исходной (16) в смысле устойчивости. При дескрипторном подходе 𝑥˙(𝑡) не заменяется на правую часть дифференциального уравнения.

Рассмотрим стандартную функцию Ляпунова:

где 𝑃2 ∈ R 𝑛×𝑛, 𝑃3 ∈ R 𝑛×𝑛 – произвольные матричные переменные.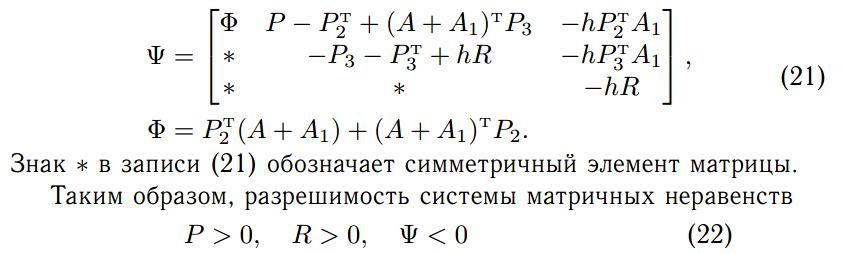

означает асимптотическую устойчивость тривиального решения системы (16) при верхней границе запаздывания равной ℎ. Если предположить, что верхняя граница запаздывания ℎ неизвестна, то матричное неравенство Ψ не является линейным. Если мы хотим найти верхнюю границу величины запаздывания, при которой тривиальное решение системы будет устойчивым, мы можем фиксировать и постепенно увеличивать ℎ до тех пор, пока система линейных матричных неравенств (22) не перестанет быть разрешимой.

Лабораторная 3

Бифуркация – это явление, при котором малое изменение параметра (или параметров) динамической системы приводит к изменению характера её решений.
Лабораторная 2 Нелинейные

Конечное время ухода решения на бесконечность. Множественность состояний равновесия. Существуют нелинейные системы, которые могут колебаться с фиксированной амплитудой и частотой вне зависимости от начальных условий этих систем. Этот тип колебаний известен как автоколебания. Бифуркации.

Рассмотрим нелинейную систему:

1) Проблема существования. Решение нелинейной системы может существовать не на всем рассматриваемом промежутке времени. 2) Проблема единственности. На рассматриваем промежутке времени у нелинейной системы может быть несколько решений.

Теперь введем определения положения равновесия. Точка (𝑥 * , 𝑢* , 𝑦* ) называется положением равновесия, если решение, начинающееся в этой точке, остается в ней же (траектория состоит из одной точки). Для поиска положений равновесия нужно приравнять производные к нулю.

У нелинейной системы может быть несколько положений равновесия, поэтому каждое из них можно исследовать на локальную устойчивость. В случае, если нелинейная система имеет единственное положение равновесия, то оно может быть глобально асимптотически устойчиво. Теперь поговорим о методах исследования устойчивости нелинейных систем.

Пусть

Положение равновесия 𝑥 * = 0 называется локально устойчивым, если для любого 𝜀 > 0 существует 𝛿(𝜀) > 0 такое, что, если ‖𝑥(0)‖ < 𝛿, то ‖𝑥(𝑡)‖ < 𝜀, ∀𝑡 > 0.

Положение равновесия 𝑥 * = 0 называется локально асимптотически устойчивым, если существует 𝛿 > 0 такое, что, если ‖𝑥(0)‖ < 𝛿, то lim𝑡→∞ 𝑥(𝑡) = 0.

Положение равновесия 𝑥 * = 0 называется глобально асимптотически устойчивым, если для любых начальных данных 𝑥(0) выполнено lim𝑡→∞ 𝑥(𝑡) = 0.

Линеаризацией называется метод приближённого представления нелинейных систем, при котором исследование нелинейной системы заменяется анализом линейной системы, в некотором смысле эквивалентной исходной. Путем замены координат ∆ = 𝑥 − 𝑎 можно получить линейный аналог исходной нелинейной системы:

В качестве точки 𝑎 будем выбирать положения равновесия нелинейной системы и каждую полученную линейную систему будем исследовать на устойчивость. Если вектор функция то:

Имеет место следующая теорема. Пусть 𝑎 – положение равновесия нелинейной системы (4), а (5) - линеаризованная возле этого положения равновесия система. Обозначим 𝛼(𝐴) = max Re(𝜆(𝐴)). Тогда

Для системы второго порядка: x1 x2

Вблизи точек равновесия «нелинейная система»≡«линейная система» Если линеаризованная возле положения равновесия система ∆ = ˙ 𝐴∆ имеет фокус, узел или седло, то исходная система 𝑥˙ = 𝑓(𝑥) имеет тот же тип точки равновесия. Если линеаризованная система имеет центр, то нелинейная система имеет либо центр, либо фокус.

ПРЕЗЕНТАЦИЯ - КУДА ВРАЩЕНИЕ

Страница 67 - линейные матричные неравенства. Важно.

АНАЛИЗ ГЛОБАЛЬНОЙ УСТОЙЧИВОСТИ

Имеет место следующая теорема. Если существует функция Ляпунова 𝑉 (𝑥) такая, что 𝑉˙ (𝑥) < 0 ∀𝑥 ∈ R 𝑛 ∖ {0}, то положение равновесия 𝑥 * ≡ 0 нелинейной системы (10) является глобально асимптотически устойчивым. Если существует функция Ляпунова 𝑉 (𝑥) такая, что 𝑉˙ (𝑥) ≤ 0 ∀𝑥 ∈ Ω ⊂ R 𝑛, то положение равновесия 𝑥 * ≡ 0 нелинейной системы (10) является локально устойчивым в области Ω.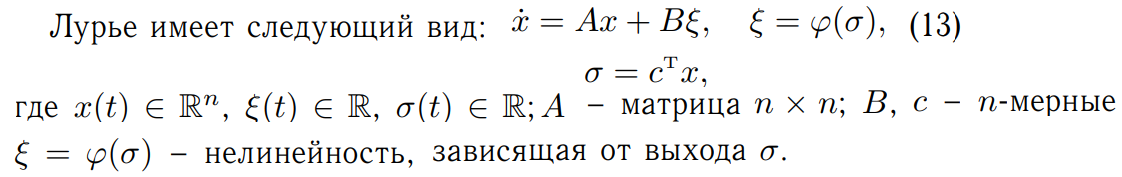

Причем первый критерий (круговой критерий) устанавливает так называемую экспоненциальную устойчивость нулевого решения. Определение экспоненциальной устойчивости следующее.

Если ∃ 𝑐 > 0, 𝜀 > 0 такие, что ∀𝑥(𝑡) системы (13) и ∀𝑡 > 𝑡0 выполнено ‖||𝑥(𝑡)|‖ ≤ 𝑐‖||𝑥(𝑡0)‖𝑒 −𝜀(𝑡−𝑡0)|| , то нулевое решение системы (13) является экспоненциально устойчивым. Это определение означает, что любое решение системы стремится к нулю с экспоненциальной скоростью.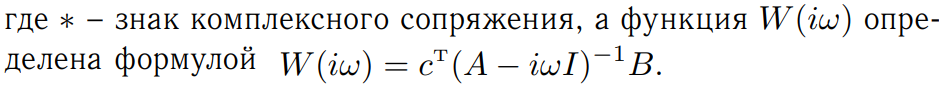