Решение. Решение Для системы, состоящей из скамьи со стоящим на ней человеком и стержнем, выполняется закон сохранения момента импульса LJconst, где jмомент инерции относительно оси вращения, угловая скорость
 Скачать 76 Kb. Скачать 76 Kb.
|
|
1. В центре скамьи Жуковского стоит человек и держит в руках вертикально тонкий однородный стержень массой m и длиной l так, что центр масс человека со стержнем находится на оси вращения скамьи. Платформа (скамья) массой m1, представляющая собой сплошной диск радиуса R, вращается с угловой скоростью вокруг вертикальной оси. Определить: во сколько раз изменится частота вращения платформы, если человек переместился из центра к ее краю на половину радиуса платформы, не меняя расположение стержня. Считать человека материальной точкой массой m3=66,0 кг по сравнению с размерами платформы; m=4,0 кг, m1=100,0 кг. Решение: Для системы, состоящей из скамьи со стоящим на ней человеком и стержнем, выполняется закон сохранения момента импульса: L=J*ω=const, где J-момент инерции относительно оси вращения, ω-угловая скорость Тогда можно записать: J1*ω1= J2* ω2 Цифрой 1 обозначен момент импульса системы с человеком, стоящим на скамье до перемещения, 2-после перемещения из центра к краю на половину радиуса платформы В первом состоянии момент импульса системы равен моменту импульса платформы за счет того, что момент импульса человека равен нулю (так как он находится в центре платформы, где его момент инерции как материальной точки равен нулю, поскольку ось вращения проходит через него).Поэтому L1=2π*n1* Jпл Во втором состоянии момент импульса системы состоит из момента импульса платформы и момента импульса, человека, стоящего на краю платформы, т.е. L2=Lпл+ Lчел=Iпл*ω2+Iчел*ω2=2π*n2 *(Jпл+ Jчел) Так как: L1= L2 2π*n1* Jпл1=2π*n2 *( Jпл2+ Jчел2) Найдем отношение частот n1/n2: n1/n2=(Jпл2+ Jчел2)/ Jпл1 Jпл1=m1*R2 Jпл2= m1*R2 Jчел2= m3*R2 n1/n2=( m1*R2+ m3*R2)/ m1*R2=1+m3/ m1 Найдем n2/n1=1/(1+m3/ m1)=1/(1+66/100)=1/1,66=0,602, n2=0,6*n1 Ответ: частота вращения будет равна n2=0,6*n1 Ответ: 2. Два маятника: пружинный, представляющий собой груз массой m1, подвешенный на невесомой пружине с коэффициентом упругости k, и физический - однородный тонкий стержень длиной l и массой m2. Ось качания физического маятника горизонтальна и проходит на расстоянии x от верхнего конца стержня, к нижнему концу которого прикреплен точечный груз массой m3. Определить: период затухающих колебаний физического маятника, если коэффициент затухания =2,0х10-2 с-1, l=1,0 м, m2=2,0 кг, х=0, m3=2,0 кг. Решение: Период для затухающих колебаний равен: T=2π/ω=2π/( ω02-2)0,5, где ω0-частота колебаний, -коэффициент затухания. Собственная частота колебаний для математического маятника равна ω0=(m2*g*l/J)0,5, где J-момент инерции физического маятника l-расстояние от точки подвеса до центра масс, в данном случае оно равно длине стержня Момент инерции мятника равен: J=m2l2 Тогда частота равна: ω0=(m2*g*l/ m2l2)0,5=(g/l)0,5=(9,8/1)0,5=9,13 с-1 Период затухающих колебаний равен: T=2π/( ω02-2)0,5=2*3,14/(9,132-4*10-4)0,5=6,28/9,13=0,688 с Ответ: T=0,688 с 3. Плоская косинусоидная бегущая волна с циклической частотой распространяется без затухания в направлении ОХ со скоростью v и имеет амплитуду смещения А. После отражения от рефлектора возникает отраженная плоская волна той же амплитуды, движущаяся навстречу падающей. Определить: координаты узлов стоячей волны, возникшей в результате интерференции падающей и отраженной волн, а также расстояние между ближайшими узлами, если = с-1, v=20,0 м/с. Решение: Уравнение бегущей волны, распространяющейся вдоль положительного направления оси х (т.е. уравнение падающей волны): Уравнение бегущей волны, распространяющейся в отрицательном направлении оси х (т.е. уравнение отраженной волны): Складывая эти уравнения, получим выражение для стоячей волны: 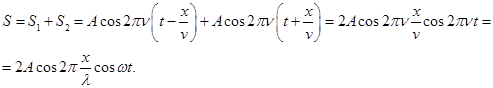 Особенностью стоячей волны является то, что амплитуда зависит от координаты х. При перемещении от одной точки к другой амплитуда меняется по закону: Расстояние между двумя соседними узлами равно Найдем длину волны: Волновое число k=/ v=2/λ Найдем из этого выражения длину волны λ λ = v*2/= v*2/= 2*v=40 м Таким образом, расстояние между двумя соседними узлами равно λ/2=20 м. Узлы стоячей волны-это точки, в которых амплитуда колебаний равна нулю, т.е.: X y=±1/2*20=±10 (m=0) X y=±3/2*20=±30 (m=1) X y=±5/2*20=±50 (m=1) и т.д. Ответ: координаты узлов: X y=±10 (m=0), X y=±30 (m=1), X y=±50 (m=1), расстояние между двумя соседними узлами равно20 м. 4. Два сферических баллона, внутренние радиусы которых r1 и r2, соединены трубкой пренебрежимо малого объема, снабженной закрытым вентилем. В баллонах находится азот под давлением соответственно р1 и р2 при единой температуре t1. считая газ идеальным, определить: среднюю длину свободного пробега молекул азота в баллонах после соединения их с помощью вентиля и понижения температуры до t2=170C, если r1=0,50 м, r2=0,25 м, р1=2,0 мм рт.ст., р2=1,1х105 Па, t1=270C, эффективный диаметр молекул азота d=3,0*10-10 м. Решение: 1) Переведем давление р1 в Паскали: 760 мм рт.ст.-105 Па 2,0 мм рт.ст.-x x= р1=(2,0*105)/760=2,63*102 Па 2) Длина свободного пробега молекул λ – это расстояние, которое проходит молекула между двумя последовательными столкновениями. Рассчитывается по формуле: <λ>=1/(2)0,5 π*d2*n, где d-эффективный диаметр молекулы, n-число молекул в единице объема Концентрацию молекул n выразим из соотношения: P=n*K*T, где p-давление газа, K-постоянная Больцмана, равная 1,38*10-23 Дж/К, n = P/ K*T Давление после открытия вентиля найдем по закону Дальтона: P=p1+p2=1,1*105+2,63*102=1,103*105 Па <λ>= (K*T)/(2)0,5π*d2*p=1,38*10-23*(17+273)/(2)0,5*3,14*(3,0*10-10)2* 1,103*105=4*10-21/4,408*10-14=9,074*10-8 м Ответ: <λ>=9,074*10-8 м 5. Кислород в цилиндре под поршнем совершает замкнутый цикл. Из состояния 1 с основными параметрами р1=1,2х105 Па, v1=2,0 л, Т1=300 К газ переходит адиабатически во 2 состояние так, что его объем возрастает вдвое; затем его изобарически нагревают до начальной температуры Т1 и, наконец, изотермически возвращают в исходное состояние. Считая газ идеальным, определить: работу, совершенную газом при изотермическом сжатии 4-1 (по-видимому, опечатка, 3-1). Решение: 1) Процесс 1-2- адиабатический, описывается уравнением p1*V1γ= p2*V2γ, причем V2=2 V1=4 л p1/ p2=(2 V1/ V1)γ=2γ или T*Vγ-1=const 2) Процесс 2-3- изобарное нагревание до температуры Т1 при p=const (p2=p3) V2/T2=V3/T3 3) Процесс 3-1- изотермическое сжатие, T=const (T3=T1=300 K) P3*V3= P1*V1 4) Работа при изотермическом сжатии рассчитывается по формуле: A=n*R*T1*lnV1/V3 Количество вещества n кислорода найдем по уравнению Менделеева-Клапейрона: P1*V1=n*R*T1 n = P1*V1/ R*T1=(1,2*105*2*10-3)/8,314*300=2,4*102/2494,2=0,0962 моль 5) Объем V3 найдем, из соотношения для процесса 2-3 или 3-1, предварительно рассчитав все рабочие параметры во всех точках цикла. Коэффициент адиабаты γ для кислорода, как двухатомного газа, равен 1,4 p1/ p2=2 1,4 p2= p1/2 1,4=1,2*105/2 1,4=4,55*104 Па= p3 T1*V1γ-1= T2*V2γ-1, T1/ T2=2γ-1 T2= T1/2γ-1=300/2 0,4=227,4 K V2 найдем по уравнению Менделеева-Клапейрона: V2=n*R*T2/p2=0,0962*8,314*227,4/4,55*104=3,99*10-3 м3 V3= P1*V1/p3=1,2*105*2*10-3/4,55*104=5,27*10-3 м3 Работа для изотермического процесса 3-1 равна: A 3-1=n*R*T1*lnV1/V3=0.0962*8,314*300*ln2/5,27=-232,5 Дж Ответ: A 3-1=-232,5 Дж |
