Физика задачи. Необходимо согласно методички выполнить 4 задачи 9-го варианта (. Решение. Уравнение гармонических колебаний Где амплитуда колебаний циклическая частота период колебаний
 Скачать 116.26 Kb. Скачать 116.26 Kb.
|
|
Необходимо согласно методички выполнить 4 задачи 9-го варианта. 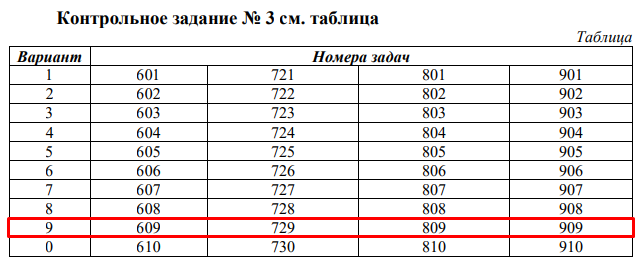 609. Для материальной точки массой m написать уравнение синусоидальных колебаний, происходящих с периодом 0,8 с и начальной фазой π/2. Найти массу материальной точки, если максимальная сила, действующая на неё равна 12 мН, а полная энергия колебаний составляет 120 мкДж. Решение. Уравнение гармонических колебаний 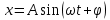 Где 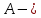 амплитуда колебаний амплитуда колебаний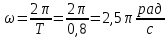 – циклическая частота – циклическая частота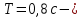 период колебаний период колебаний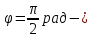 начальная фаза начальная фазаСкорость точки при гармонических колебаниях 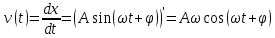 Очевидно, что модуль максимальной скорости может быть только тогда, когда тригонометрическая функция по модулю равна 1, т.е. 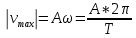 Полная энергия точки равна 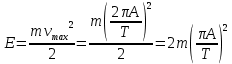 Отсюда амплитуда колебаний 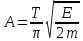 Ускорение точки при гармонических колебаниях 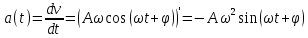 Очевидно, что максимальное ускорение возможно только при 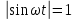 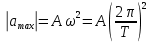 Согласно второму закону Ньютона возвращающая сила 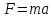 Максимальная возвращающая сила 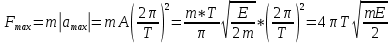 Отсюда масса материальной точки 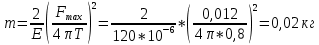 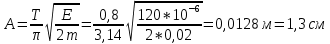 Уравнение колебаний 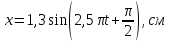 729. На дифракционную решётку нормально падает монохроматический свет с длиной волны λ = 600 нм. Определите наибольший порядок спектра, полученный с помощью этой решётки и угол дифракции, соответствующей последнему максимуму, если её постоянная d = 2 мкм. Решение. 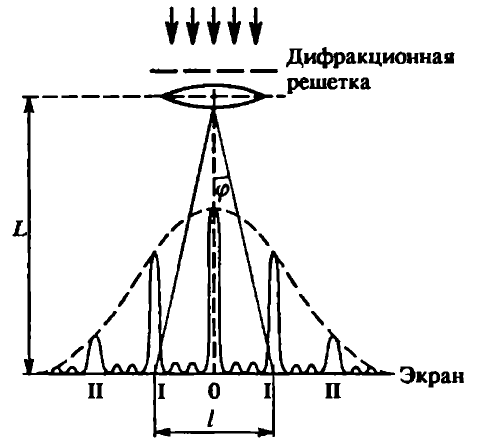 Условие дифракционных максимумов 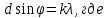 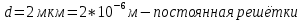 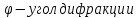 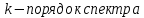 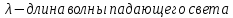 Из этой формулы очевидно, что максимальный порядок спектра может быть при 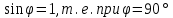 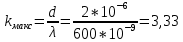 Округляем в меньшую сторону, т.е. 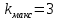 Определим общее число максимумов дифракционной картины, полученной посредством дифракционной решётки. Влево и вправо от центрального максимума будет наблюдаться по одинаковому числу максимумов, равному 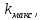 т.е. всего т.е. всего 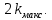 Если учесть также центральный нулевой максимум, получим общее число максимумов Если учесть также центральный нулевой максимум, получим общее число максимумов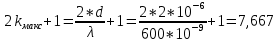 Округляем в меньшую сторону, т.е. 7. Найдём угол отклонения последнего максимума 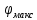 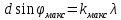 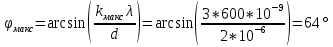 809. Масса фотонов, соответствующих максимальному значению излучательной способности абсолютно чёрного тела, равна 3 ∙ 10–36 кг. Определить температуру тела и энергию, излучаемую им за 1 секунду с 1 см2 поверхности. Решение. Мощность излучения 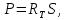 Где 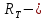 энергия, излучаемая за 1 секунду с единицы поверхности абсолютно чёрного тела, определяется формулой Стефана-Больцмана энергия, излучаемая за 1 секунду с единицы поверхности абсолютно чёрного тела, определяется формулой Стефана-Больцмана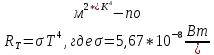 стоянная Стефана-Больцмана стоянная Стефана-Больцмана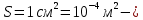 площадь поверхности тела площадь поверхности телаЭнергия, излучаемую телом за время 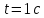 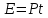 Уравнение Эйнштейна 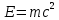 Где 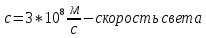 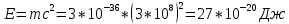 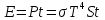 Отсюда температура 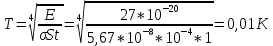 909. В одномерной прямоугольной потенциальной яме шириной l находится частица в невозбуждённом состоянии. Найти вероятность пребывания частицы в последней четверти ямы. Дать графическую иллюстрацию найденной вероятности. Решение. Собственное значение энергии частицы, находящейся на n-м энергетическом уровне в бесконечно глубоком прямоугольном потенциальном ящике  Где  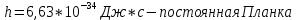 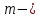 масса частицы масса частицы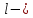 ширина потенциального ящика ширина потенциального ящикаВ случае нахождения частицы в одномерной потенциальной яме решение уравнения Шрёдингера – волновая функция 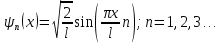 - номер энергетического уровня - номер энергетического уровняВ нашем случае 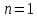 , т.к. это основное состояние по условию задачи , т.к. это основное состояние по условию задачиПлотность вероятности нахождения частицы 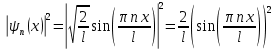 Вероятность нахождения частицы в интервале от 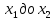 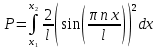 Сначала вычислим неопределённый интеграл 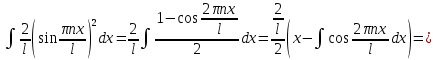 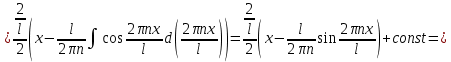 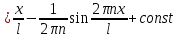 Частица в крайней четверти ящика 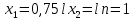 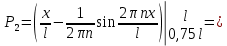 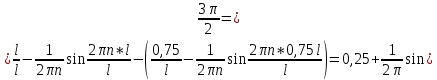 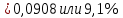 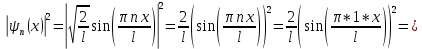 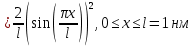 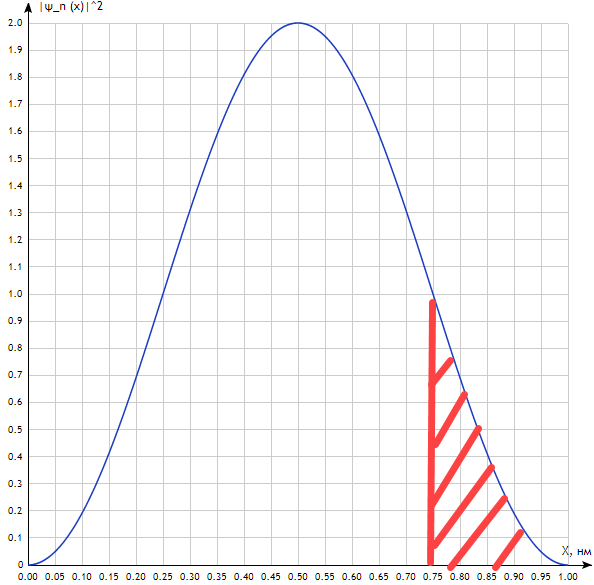 Как известно из математики, интеграл численно равен площади, т.е. заштрихованная площадь и есть искомая вероятность. |
