Вестник КарГУ_Кутум_Шайхова. Решение двумерной цепочки qТоды
 Скачать 60.58 Kb. Скачать 60.58 Kb.
|
|
УДК 530.182 Б.Б. Кутум, Г.Н. Шайхова Евразийский Национальный университет им. Л.Н. Гумилева, Астана (kuttykadam@mail.ru) q-солитонное решение двумерной цепочки q-Тоды Статья посвящена исследованию двумерной цепочки q-Тоды. Цепочка Тоды является нелинейным эволюционным уравнением, описывающим бесконечную систему масс на линии, которые взаимодействуют через экспоненциальную силу. В работе проведен анализ построения солитонного решения цепочки q-Тоды в двумерном пространтсве. Для этой цели взято уравнение движения и использовано преобразование зависимой переменной для преобразования нелинейного уравнения в билинейную форму, которая записана как полином оператора Хироты. Как один из наиболее эффективных методов построения многосолитонных решений интегрируемых нелинейных эволюционных уравнений, данный метод применим к широкому классу уравнений, включая нелинейные дифференциальные, нелинейные дифференциально-разностные уравнения. Применяя метод Хироты, была получена билинейная форма для двумерной цепочки q-Тоды на основе, которой найдено q-солитонное решение. Представлена динамика q-солитонного решения двумерной цепочки q-Тоды. Отметим, что солитон сохраняется благодаря равновесию между действием нелинейной среды с дисперсией. Помимо этого солитон ведет себя как частица: не разрушается при взаимодействии друг с другом или другими возмущениями, при этом сохраняет структуру и продолжает движение. Такое качество имеет возможность использования при передаче данных или информации на дальние расстояния практически без помех. Кроме того, исследование цепочки Тоды и применение к ней разных методов в различных размерностях позволяет перейти к пониманию таких сложных терминов как матричные модели, которые можно применить для описания разных физических систем. Ключевые слова: дисперсия, солитон, цепочка Тоды, билинейная форма, метод Хироты. Введение Волны, описываемые разными нелинейными дифференциальными уравнениями, которые состоят из особых импульсов, имеют свойство сохранения своей изначальной формы подобно стабильным частицам. Их называют уединенными волнами, одиночными волновыми частицами или солитонами. В нелинейных решетках или цепочках также имеются солитоны. Когда энергия не очень велика нелинейные цепочки ведут себя периодически, в таких нелинейных непрерывных системах распространяются устойчивые импульсы. Факт существования таких цепочек показывает, что должна существовать некоторая нелинейная цепочка, которая допускает строгие периодические волны, а определенные импульсы будут устойчивыми. Одним из таких примеров является уравнение цепочки Тоды. Цепочка Тоды является нелинейным эволюционным уравнением, описывающим бесконечную систему масс на линии, которые взаимодействуют через экспоненциальную силу. Сама по себе цепочка Тоды рассматривается как простая модель нелинейного одномерного кристалла в физике твердого тела. Он задается цепочкой частиц с взаимодействием ближайшего соседа, описываемой уравнениями движения [1]. В различных источниках для поиска точных решений нелинейных дифференциальных уравнений, предлагают огромное количество методов, такие как преобразование Бэклунда [2], метод Хироты [3], обратное преобразование рассеяния [4] и другие. Одним из наиболее эффективных методов построения солитонных решений интегрируемых нелинейных эволюционных уравнений является прямой метод Хироты, с которым можно ознакомиться в [3]. Данный метод применим к широкому классу уравнений, включая нелинейные дифференциальные, нелинейные дифференциально-разностные уравнения [5-7]. Начальным этапом данного метода является использование преобразования зависимой переменной для преобразования нелинейного уравнения в частных производных в квадратичную форму, так называемую билинейную форму. Основная идея метода заключается в том, чтобы записать билинейную форму как полином оператора Хироты - D. Эта компактная форма называется билинейной формой Хироты. Следует отметить, что нелинейные уравнения в частных производных или дифференциально-разностные могут иметь не только билинейные формы Хироты, а также трилинейные или полилинейные формы [8]. Предполагается, что все полностью интегрируемые нелинейные уравнения в частных производных или разностные уравнения могут быть записаны в билинейной форме Хироты. С другой стороны, для уравнения, допускающего билинейную форму Хироты, не гарантируется существование N-солитонных решений любого порядка. Уравнения, допускающие билинейную форму Хироты и имеющие N-солитонные решения, называются интегрируемыми по Хироте [9]. В данной работе представляем двумерную цепочку q-Тоды, одномерный случай был рассмотрен в работе [10]. С помощью билинейного метода Хироты находим билинейную форму двумерной цепочки q-Тоды, на основе которой получаем, дисперсионное соотношение и солитонное решение. Двумерная цепочка q-Тоды Изначально классическая механика изучалась именно для одномерных цепочек, где образующие их частицы взаимодействуют только с ближайшими соседями. Если ограничить их рассмотрение только однородными системами, то массу каждой частицы обозначим 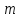 , смещение , смещение 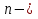 ой частицы ой частицы 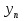 , а потенциал взаимодействия между соседними частицами , а потенциал взаимодействия между соседними частицами 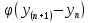 . Тогда уравнение движения принимает следующий вид . Тогда уравнение движения принимает следующий вид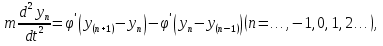 (1) (1)где 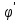 производная производная 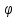 . Таким образом, . Таким образом,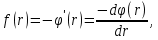 (2) (2)есть сила, с которой действует пружина, растянутая на величину 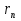 , где , где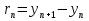 или или 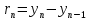 (3) (3)(3) – это относительное смещение. Когда сила 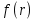 пропорциональна смещению пропорциональна смещению 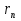 выполняется закон Гука. Уравнение Тоды [10], описывающее движения ангармонической решетки, имеет вид выполняется закон Гука. Уравнение Тоды [10], описывающее движения ангармонической решетки, имеет вид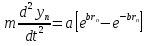 , (4) , (4)где 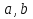 и и 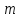 реальные константы. Вводя силу реальные константы. Вводя силу 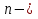 ой частицы в решетку, получаем следующее уравнение ой частицы в решетку, получаем следующее уравнение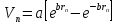 , (5) , (5)как быстро убывающая функция, уравнение (4) оказывается 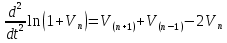 . (6) . (6)Двумерную цепочка q-Тоды имеет следующий вид 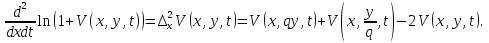 (7) (7)Введем преобразование зависимой переменной как 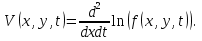 (8) (8)Подставляя (8) в (7) и дважды интегрируя полученное выражение, получим 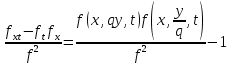 , (9) , (9)Уравнение (9) можно преставить в билинейной форме Хироты, а именно в терминах D-оператора Хироты, как 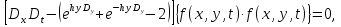 (10) (10)что следует из (9) путем умножения на 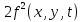 , где мы используем q-экспоненциальное тождество. Для произвольных непрерывно дифференцируемых функций , где мы используем q-экспоненциальное тождество. Для произвольных непрерывно дифференцируемых функций 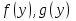 q-экспоненциальная единица будет [10] q-экспоненциальная единица будет [10]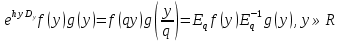 (11) (11)Последнее уравнение выполняется там, где мы имеем обычное соотношение между двумя квантовыми параметрами 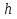 и и 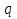 при при 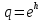 . Чтобы найти солитонные решения цепочки Тоды, применяем разложение возмущений вокруг формального параметра возмущения . Чтобы найти солитонные решения цепочки Тоды, применяем разложение возмущений вокруг формального параметра возмущения 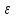 в виде в виде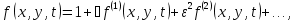 (12) (12)Подставив (12) в (10) получим уравнение 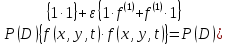 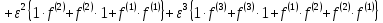 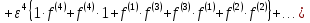 , (13) , (13)где 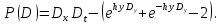 Собираем коэффициенты по Собираем коэффициенты по 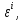 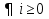 уравнения (13). Коэффициент первого слагаемого уравнения (13). Коэффициент первого слагаемого 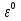 тривиально исчезает, а из коэффициента тривиально исчезает, а из коэффициента 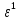 имеем имеем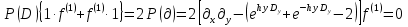 , (14) , (14)(14)-уравнение является прямым результатом свойства оператора Хироты D [9], поскольку 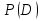 имеет четный порядок. Следующим важным этапом расчета является поиск решения уравнения (14). имеет четный порядок. Следующим важным этапом расчета является поиск решения уравнения (14).Общая тенденция для солитонных решений носит экспоненциальный характер, однако экспоненциальная функция 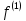 не удовлетворяет уравнение (14). Из-за природы q-чисел решение уравнения (14) должно иметь степенную функцию для аналога q-дискретной пространственной переменной. Поэтому можно выбрать исходное решение (14) как не удовлетворяет уравнение (14). Из-за природы q-чисел решение уравнения (14) должно иметь степенную функцию для аналога q-дискретной пространственной переменной. Поэтому можно выбрать исходное решение (14) как 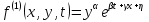 , (15) , (15)где, 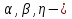 произвольные константы. произвольные константы. Решение, обладающее обычным поведением солитонов и имеющее степенные аналоги для q-дискретных переменных, называется q-солитонным решением. Если подставить (15) в (14), получим соотношение между параметрами 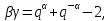 (16) (16)(16)-уравнение называется дисперсионным соотношением. Коэффициент 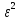 , полученный из (13), дает следующее , полученный из (13), дает следующее 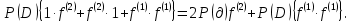 Что дает явное 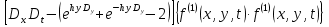 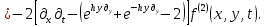 (17) (17)Отметим, что поскольку 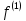 , данное в (14) удовлетворяет форме (17), мы можем допустить, что все члены более высокого порядка равны нулю, т.е. , данное в (14) удовлетворяет форме (17), мы можем допустить, что все члены более высокого порядка равны нулю, т.е. 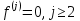 . Далее как обобщение этот факт можно предположить при выводе i-q-солитонного решения, . Далее как обобщение этот факт можно предположить при выводе i-q-солитонного решения, 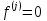 для всех для всех 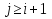 . При . При 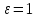 , строим одно-q-солитонное решение, подставляя (15), (16) в (17) с учетом что , строим одно-q-солитонное решение, подставляя (15), (16) в (17) с учетом что 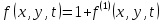 тогда тогда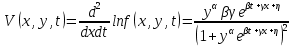 , (18) , (18)где (18) является одно-q-солитонное решение двумерной цепочки q-Тоды. Динамика одно-q-солитонного решения представлена на рисунке 1. 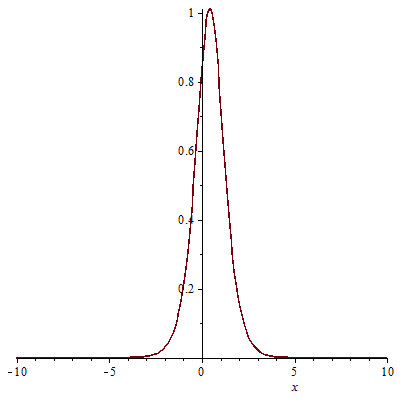 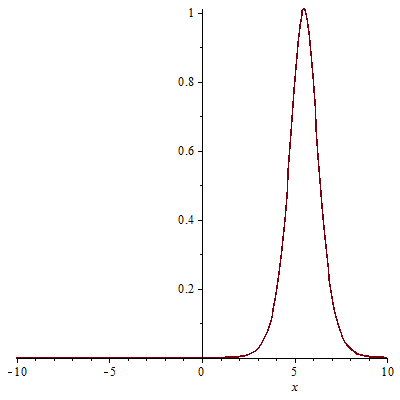 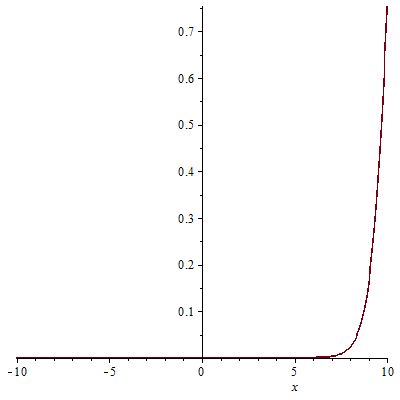 а) б) в) Рисунок 1. Динамика одно-q-солитонного решения двумерной цепочки q-Тоды с параметрами: γ=2, α=-5, η=0, q=1.25, (a) t=-5, (б) t=0, (в) t=5. Рис.1 показывает динамику полученного решения (18) в зависимости от t. Так при разных значениях t волна сохраняет свою форму. Это доказывает, что в двумерной цепочке q-Тоды имеются солитоны, то есть возможен перенос энергии. Цепочка Тоды уникальна тем, что имеет широкий диапазон от гармонического до ангормонического предела и имеет так называемые N-солитонные решения. Как было представлено выше, солитон структурно неизменная уединенная волна в нелинейной среде. Солитоны при взаимодействии между собой или другими возмущениями ведут себя подобно частицам, поэтому их и называют частицеподобными. Они сохраняют свою структуру, не разрушаясь при столкновении, благодаря равновесию между действием нелинейной среды и дисперсии. Заключение В данной работе представили цепочку q-Тоды в двумерном пространстве. С помощью билинейного метода Хироты нашли билинейную форму двумерной цепочки q-Тоды, на основе которой получили, дисперсионное соотношение и одно-q-солитонное решение. Данный алгоритм может быть применен для получения N-солитонных решений. Солитон сохраняется благодаря равновесию между действием нелинейной среды с дисперсией. Помимо этого солитон ведет себя как частица (частицеподобная): не разрушается при взаимодействии друг с другом или другими возмущениями, при этом сохраняет структуру и продолжает движение. Такое качество имеет возможность использования при передаче данных или информации на дальние расстояния практически без помех. Исследование цепочки Тоды в различных размерностях позволяет перейти к пониманию таких сложных терминов как матричные модели, которые можно применить для описания разных физических систем. Работа выполнена в рамках финансовой поддержки научно-технической программы (Ф.0811, № 0118РК00935) МОН РК. Список литературы
Б.Б. Кутум, Г.Н. Шайхова Екі өлшемді q-Тода тізбегінің q-солитондық шешімі Мақала екі өлшемді q-Тода тізбегін зерттеуге арналған. Тода тізбегі экспоненциалдық күш арқылы өзара әрекеттесетін, сызықтағы шексіз массалар жүйесін сипаттайтын сызықты емес эволюциялық теңдеу болып табылады. Жұмыста q-Тода тізбегінің екі өлшемді кеңістіктегі солитондық шешімін құрастыру талданды. Мақсатқа қолжеткізу үшін қозғалыс теңдеуі алынып, Хирота полиномы ретінде жазылған бисызықты түрге келтіру үшін сызықты емес теңдеуді тәуелді айнымалыны түрлендіру қолданды. Интегралданатын сызықты емес эволюциялық теңдеулердің көп солитонды шешімдерін құрастырудың тиімді әдістерінің бірі ретінде, берілген әдісті көптеген теңдеулерге, олардың ішінде сызықты емес дифференциал, сызықты емес дифференциал-айырымдық теңдеулерге қолдануға болады. Хирота әдісін қолдана отырып, екі өлшемді q-Тода тізбегінің бисызықты түрі алынып, оның негізінде q-солитондық шешімі есептелді. Екі өлшемді q-Тода тізбегінің q-солитондық шешімнің динамикасы ұсынылды. Атап айтқанда, солитон сызықты емес орта мен дисперсия арасындағы әрекетінің тепе-теңдігі арқасында сақталады. Сонымен қатар солитон өзін бөлшек ретінде ұстайды: бір-бірімен немесе басқа ауытқулармен өзара әрекеттесу кезінде қирамай, құрылымын сақтап қозғалысын жалғастырады. Осындай қасиетті мәліметті немесе ақпаратты алысқа дерлік кедергісіз жіберу кезінде қолдануға мүмкіндік туғызады. Бұдан басқа, Тода тізбегін және оған түрлі өлшемділіктегі әртүрлі әдістердің қолдануын зерттеу әркелкі физикалық жүйелерді сипаттау мақсатында қолдануға болатын, матрицалық модельдер сияқты күрделі терминдерді түсінуге мүмкіндік туғызады. Түйін сөздер: оңашаланған толқын, Тода тізбегі, бір солитондық шешім, бисызықты түрі, Хирота әдісі. B.B. Kutum, G.N. Shaikhova q-soliton solution of a two-dimensional q-Toda chain The article is devoted to the investigation of the two-dimensional q-Toda chain. The Toda chain is a non-linear evolution equation describing an infinite system of masses on a line that interact through an exponential force. The paper analyzes the construction of a soliton solution of the q-Toda chain in a two-dimensional space. For this purpose, the equation of motion is taken and the transformation of the dependent variable is used to convert the nonlinear equation into a bilinear form, which is written as the Hirota polynomial. As one of the most effective methods for constructing multisoliton solutions of integrable nonlinear evolution equations, this method is applicable to a wide class of equations, including nonlinear differential, nonlinear differential-difference equations. Using the Hirota method, a bilinear form was obtained for the two-dimensional q-Toda chain on the basis of which the q-soliton solution was found. The dynamics of the q-soliton solution of a two-dimensional q-Toda chain is presented. Note that the soliton is conserved due to the equilibrium between the action of a nonlinear medium with dispersion. In addition, the soliton behaves like a particle: does not collapse when interacting with each other or other disturbances, while maintaining the structure and continues to move. This quality has the ability to use when transferring data or information over long distances with virtually no interference. In addition, the study of the Toda chain and the application to it of different methods in different dimensions allows one to proceed to the understanding of such complex terms as matrix models that can be used to describe different physical systems. Keywords: solitary wave, Toda chain, one-soliton solution, bilinear form, Hirota method. References
|
